RSA演算法理論學習解惑――複製貼上RSA私鑰導致tengine出錯深入解析
轉自:https://yq.aliyun.com/articles/601036
原創文章:來自RSA演算法理論學習解惑――複製貼上RSA私鑰導致tengine出錯深入解析
tengine的程式碼中使用了RSA_check_key函式進行RSA私鑰格式正確性檢查,有一次載入私鑰測試時tengine reload失敗。案例的看點是RSA格式私鑰檔案中的私鑰指數d在tengine實際的加解密計算過程中並沒有用到,至於為什麼請細看下文。
問題背景
在一次配置tengine https服務使用的證書和私鑰操作時採用了從原檔案複製貼上的方式,當使用tengine啟動服務時提示出錯:
$tengine -c tengine.conf –t nginx: [emerg] RSA private key broken: /xxxx/4ed20dc594d0d75926f517d2b29879e2 140319033337512:error:0407B07B:rsa routines:RSA_check_key:d e not congruent to 1:rsa_chk.c:175: 140319033337512:error:0407B07C:rsa routines:RSA_check_key:dmp1 not congruent to d:rsa_chk.c:194: 140319033337512:error:0407B07D:rsa routines:RSA_check_key:dmq1 not congruent to d:rsa_chk.c:212:
關鍵性提示背後的含義未知。
d e not congruent to 1
dmp1 not congruent to d
dmq1 not congruent to d
原因分析
排查過程中疑問如下:
- 從上述提示可以得知rsa_chk.c的行數,從而找到呼叫來源是tengine中RSA_check_key函式,
if (RSA_check_key(pkey) != 1) { ngx_log_error(NGX_LOG_EMERG, ctx->log, 0, "RSA private key broken: %V", name); ERR_print_errors_fp(stderr); RSA_free(pkey); ret = NGX_ABORT; goto out; }
- 排查此使用者的證書與私鑰的正確性,首先檢視私鑰的格式與輸出:
- rsa -in 111.pem –text 測試正常沒有錯誤
$openssl s_server -accept 9999 -cert cert.crt -key 111.pem
Using default temp DH parameters
Using default temp ECDH parameters然後用curl訪問https://127.0.0.1:9999埠後, 上述openssl s_server服務列印輸出如下:
ACCEPT GET / HTTP/1.1 User-Agent: curl/7.29.0 Host: localhost:9999 Accept: */*
即ssl握手過程中用到證書與私鑰能驗證通過!應該能說明證書與私鑰確實是配對的。這不可能太奇怪了?!
最後用openssl rsa -in 111.pem –check 才發現有問題。到底是什麼原因tengine 判斷私鑰有問題?本著刨根問底的精神,聯絡了做openssl的幾個同事,暫時也沒有人對這塊有深入的研究。只能自己動手分析了。
首先查openssl中出錯時的程式碼塊
/* d*e = 1 mod lcm(p-1,q-1)? */
173 if (!BN_is_one(i)) {
174 ret = 0;
175 RSAerr(RSA_F_RSA_CHECK_KEY, RSA_R_D_E_NOT_CONGRUENT_TO_1);
176 }使用d和q引數計算 dmq1,然後與私鑰檔案中解出的dmq1比對檢視是否正確.
197 /* dmq1 = d mod (q-1)? */
198 r = BN_sub(i, key->q, BN_value_one());
199 if (!r) {
200 ret = -1;
201 goto err;
202 }
203
204 r = BN_mod(j, key->d, i, ctx);
205 if (!r) {
206 ret = -1;
207 goto err;
208 }
209
210 if (BN_cmp(j, key->dmq1) != 0) {
211 ret = 0;
212 RSAerr(RSA_F_RSA_CHECK_KEY, RSA_R_DMQ1_NOT_CONGRUENT_TO_D);
213 }細節分析
看來必須搞清楚這幾個引數的含義,但要搞清楚這幾個引數的作用需要了解rsa加解密的原理,建議先讀“RSA演算法原理(二)”
http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
這幾個引數在openssl中具體定義是
struct crypto_rsa_key {
int private_key; /* whether private key is set */
struct bignum *n; /* modulus (p * q) */
struct bignum *e; /* public exponent */
/* The following parameters are available only if private_key is set */
struct bignum *d; /* private exponent */
struct bignum *p; /* prime p (factor of n) */
struct bignum *q; /* prime q (factor of n) */
struct bignum *dmp1; /* d mod (p - 1); CRT exponent */
struct bignum *dmq1; /* d mod (q - 1); CRT exponent */
struct bignum *iqmp; /* 1 / q mod p; CRT coefficient */
};我以個人理解簡單點來解釋:公鑰可以用n和e代表,私鑰可以用n和d代表;且n=p*q算出,e和d需要滿足 ed ≡ 1 (mod φ(n)),其中φ(n)代表n的尤拉函式;私鑰檔案中有了這幾個引數完全可以實現用來私鑰解密和簽名等功能了。以m代表明文,c代表密文,所謂"加密"過程,就是算出下式的c:
me ≡ c (mod n)
所謂解密就是c的d次方除以n的餘數為m:
cd ≡ m (mod n)
但是直接用n d大數來直接使用存在效率不高的問題,然後就有數學大牛們引入了新的演算法-中國餘數定理,用於解決效率的問題(本文簡稱為RSA-CRT演算法)。解密和簽名的過程就改為了
https://w1.fi/cgit/hostap/plain/src/tls/rsa.c
/*
* Decrypt (or sign) using Chinese remainer theorem to speed
* up calculation. This is equivalent to tmp = tmp^d mod n
* (which would require more CPU to calculate directly).
*
* dmp1 = (1/e) mod (p-1)
* dmq1 = (1/e) mod (q-1)
* iqmp = (1/q) mod p, where p > q
* m1 = c^dmp1 mod p
* m2 = c^dmq1 mod q
* h = q^-1 (m1 - m2) mod p
* m = m2 + hq
*/即RSA-CRT演算法只需要5個元素就可以完成模冪運算,不需要用到d.現在也可以清楚了上述crypto_rsa_key結構中最後引數的含義了,即用於RSA-CRT計算用的,且dmp1 dmq1也可以通過d計算得到。
一個RSA私鑰檔案中的內容解析如下:
$openssl rsa -in serverkey.pem -text
Private-Key: (2048 bit)
modulus:
00:e3:b7:cb:15:a0:92:a2:0f:10:25:a4:cd:a8:2f:
24:95:d2:65:e1:3f:cf:4d:87:64:52:f8:d9:f9:dc:
…………
publicExponent: 65537 (0x10001)
privateExponent:
6b:39:60:c4:07:3e:e4:56:29:69:40:47:a2:38:c8:
86:4f:72:af:74:87:5d:5f:32:2b:2b:88:1f:f2:17:
……。
prime1:
00:ff:6a:2f:e3:fb:6c:3c:65:e9:03:0e:0e:8f:4b:
65:9b:26:8d:22:39:07:26:e5:ca:cc:b2:79:05:4e:
…………
prime2:
00:e4:3d:5c:57:35:26:39:18:ab:ba:c4:91:45:cd:
77:9a:f9:93:75:12:3b:50:d7:53:0b:ee:17:57:70:
…………
exponent1:
00:c9:f5:c0:0a:88:6a:ec:53:34:ed:6a:77:0e:cd:
72:79:3d:01:8a:17:07:d5:b5:0c:27:d1:d3:a9:e3:
…………
exponent2:
69:42:23:23:d4:cf:1b:e5:d4:cc:fd:7a:41:c6:d0:
32:18:87:78:a6:3f:d4:b8:79:04:37:79:6c:49:d0:
…………
coefficient:
00:c0:7a:72:d3:fe:81:de:de:3d:21:21:cc:c2:20:
a0:0e:2e:d2:91:1f:af:b3:89:a2:12:50:88:2c:c6:
…………
writing RSA key從上可以看出所有的引數都包含在私鑰檔案中。
現在可以理解RSA_check_key(pkey) 函式為什麼出錯了:即拿到私鑰檔案中dmp1,dmq1,d用公式計算他們的關係發現結果不一致所以報錯了。
與原檔案正確的私鑰經過對比發現有一個字元出錯,下圖中101行代表原始的pem格式私鑰資料C13改為了C12,第32行是經過轉換後的資料,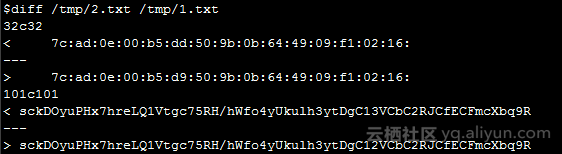
查32行得知屬於privateExponent部分,即屬於私鑰元素d

到此本該結束了,但還有一個疑問為什麼nginx與 openssl s_server都沒有出錯,追了一下openssl程式碼
rsa->meth->rsa_mod_exp()最後呼叫 RSA_eay_mod_exp()此函式實現解密沒有用到d引數。
nginx與 openssl s_server都沒有呼叫RSA_check_key函式,而tengine做載入私鑰用到了RSA_check_key函式。
推斷openssl rsa -in 111.pem –check應該也用到了此RSA_check_key函式
小結
主要是需要對RSA私鑰檔案中各引數的作用需要詳細瞭解,由於需要數論原理很多,理解openssl程式碼難度還是很高的,搞了幾個小時終於搞明白了原理。
