【AI系列】<3>生成神經網路以及初始化詳細過程
阿新 • • 發佈:2018-11-15
內容簡介
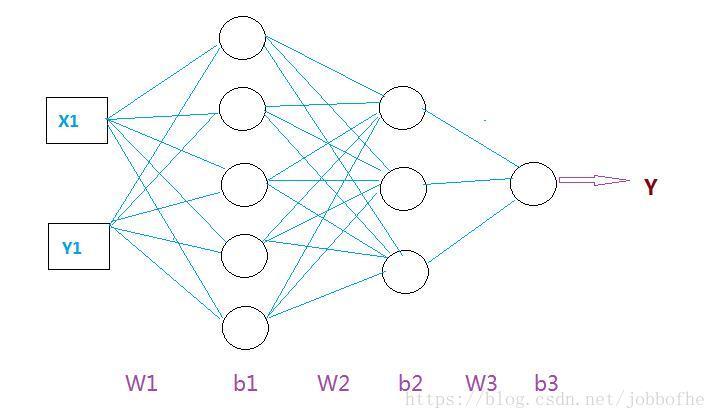
本文將會介紹神經網路的生成過程,通過生成一個[2, 5, 3, 1]的神經網路,詳細講解每一步驟的運算過程。[2, 5, 3, 1] 表示:兩個輸入,第一層 5各神經元,第二層3個神經元,第三層 1個神經元。
- 生成輸入資料
np.random.seed(1)
#畫一個圈
train_X, train_Y = sklearn.datasets.make_circles(n_samples=300, noise=.05)
# Visualize the data
plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40 我們假設輸入是一個點(x1,y1).共有300個點,這些點隨機分佈呈橢圓形。這些點組成一個矩陣就是所有輸入引數,我們用你X表示。
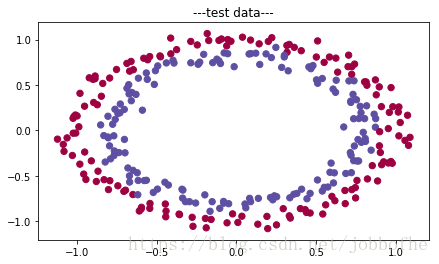
這裡生成的X是一個300*2的矩陣。如下:

對X進行轉置,得到一個2*300的矩陣,如下
- 整個網路權值初始化為0
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
""" 到這裡我們將每一層的權值都初始化為零了。現在我們來分析一下現在每一層的權值詳細情況。
第一層 W1: 5*2的矩陣
b1 :5*1 列向量
第二層 W2:3*5 矩陣
b2 :3*1
第三層 W3:1*3 矩陣
b3 : 0
前向傳播計算過程
- 前向傳播程式碼以及註釋
def forward_propagation(X, parameters):
"""
Implements the forward propagation (and computes the loss) presented in Figure 2.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape ()
b1 -- bias vector of shape ()
W2 -- weight matrix of shape ()
b2 -- bias vector of shape ()
W3 -- weight matrix of shape ()
b3 -- bias vector of shape ()
Returns:
loss -- the loss function (vanilla logistic loss)
"""
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
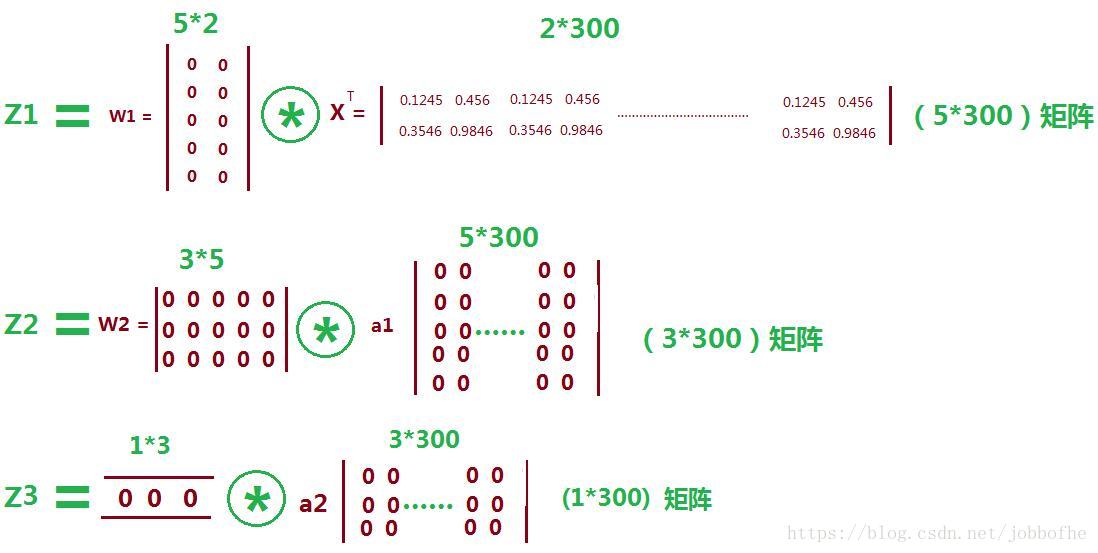
z1 = np.dot(W1, X) + b1 #W1: [5, 2] X[2, 300],矩陣乘法可乘條件:前者 列= 後者行 z1:[5,300]
a1 = relu(z1) #啟用函式
z2 = np.dot(W2, a1) + b2 #W2:[3, 5] a1[5,300] z2:[3,300]
a2 = relu(z2)
z3 = np.dot(W3, a2) + b3 #W3:[1,3] a2:[3,300] z3:[1,300]
a3 = sigmoid(z3)
cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
return a3, cache #a3 即是最後的記過Y’值,之後根據提前期望的Y值,進行誤差反向傳播。神經網路層數與權值W 的矩陣形式有以下對應形式:
假設神經網路是 [2, 10, 20, 5, 1], 很明顯這是一個2分類問題。
那麼
W1 就是 10*2 的矩陣 b1 : 10*1
W2: 20*10 b2: 20*1
W3: 5*20 b3: 5*1
W4: 1*5 b4: 1*1
相信規律已經很明白了。這裡W看做與神經元連線的每一條線,b看做每一個神經元。