1. 圖的表示

1）臨接矩陣

使用二維陣列arr[N][N]表示一個圖。

a. N 為圖的頂點個數，矩陣的對角線全為0。

b. 兩個頂點連通的話，矩陣的值為1

c. 某一行的和表示該頂點的出度。某一列的和表示該頂點的入度

d. 有權值的圖，矩陣元素不再是0,1表示是否連通，而是把元素值表示為權值。不存在的邊，權值記錄為∞；對角線上的權值為0

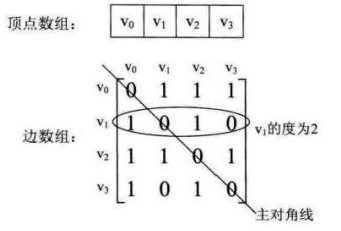
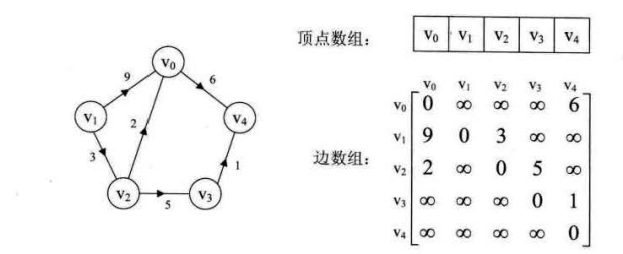
使用臨接矩陣表示圖，直觀方便，缺點是佔用空間大，因為需要 N*N 個空間。對於稀疏圖來說，這比較浪費空間。

2) 臨接表

a. 使用陣列儲存頂點

b. 每個頂點的所有臨接點組成一個線性表，掛在陣列後面。

這種方法類似散列表的開鏈法。

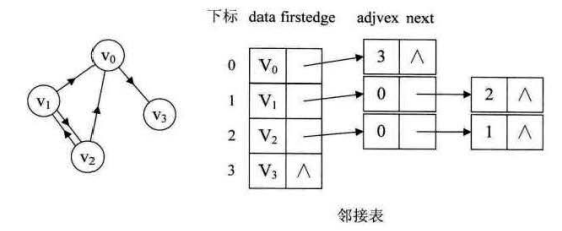
優點是節省空間，頂點的出度就在連結串列上，但是要查詢入度的話，需要遍歷整個圖

2. 圖的遍歷

1）廣度優先

先遍歷圖的所有臨節點，再依次遍歷臨接點的臨接點

2）深度優先

從某一個節點出發，一直走下去，直到找不到臨接點。再從其他節點出發，繼續一條道路走到黑

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <assert.h>


enum Ecolor
{
    WHITE 
 
= 0,
    GRAY,
    BLACK
};

// 這裡使用臨接表表示圖
struct graph_node_s
{
    enum Ecolor color;  // 節點顏色，用來標識該頂點是否別遍歷過
    int d;
    int ftime;          // 節點訪問結束時間
    int dtime;          // 節點訪問開始時間
    struct graph_node_s *next;
};
typedef struct graph_node_s graph_node_t;

struct graph_s
{
    int vertice;        //
 
 頂點數
    int edge;           // 邊數
    graph_node_t *bucket[1];    // 儲存頂點節點
};
typedef struct graph_s graph_t;

// 廣度優先遍歷使用了佇列儲存臨接點
struct queue_node_s
{
    void *d;
    struct queue_node_s *prev;
    struct queue_node_s *next;
};
typedef struct queue_node_s queue_node_t;

struct queue_s
{
    queue_node_t *sentinel;
};
typedef struct queue_s queue_t;


queue_t *queue_create(void)
{
    queue_t *queue = (queue_t*)malloc(sizeof(queue_t));
    assert(queue);

    queue->sentinel = (queue_node_t*)malloc(sizeof(queue_node_t));
    assert(queue->sentinel);

    queue->sentinel->next = queue->sentinel;
    queue->sentinel->prev = queue->sentinel;

    return queue;
}

void queue_destroy(queue_t *q)
{
    assert(q);

    queue_node_t *nd = q->sentinel->next;
    while (nd != q->sentinel)
    {
        queue_node_t *tmp = nd;
        nd = nd->next;
        free(tmp);
    }
    free(nd);
    free(q);
}

void queue_push(queue_t *q, void *value)
{
    assert(q);
    assert(value);

    queue_node_t* nd = (queue_node_t*)malloc(sizeof(queue_node_t));
    assert(nd);

    nd->d = value;
    nd->next = q->sentinel;
    nd->prev = q->sentinel->prev;
    q->sentinel->prev->next = nd;
    q->sentinel->prev = nd;
}

void queue_pop(queue_t *q)
{
    assert(q);

    queue_node_t *tmp = q->sentinel->next;

    if (tmp != q->sentinel)
    {
        q->sentinel->next = q->sentinel->next->next;
        q->sentinel->next->prev = q->sentinel;
        free(tmp);
    }
}

void *queue_front(queue_t *q)
{
    assert(q);

    return q->sentinel->next->d;
}

int queue_empty(queue_t *q)
{
    assert(q);

    return q->sentinel->next == q->sentinel;
}

graph_t *graph_create(int vertice)
{
    graph_t *g = (graph_t*)malloc(sizeof(graph_t) + (vertice-1)*sizeof(graph_node_t*));
    assert(g);

    g->vertice = vertice;
    g->edge = 0;
    for (int i = 0; i < vertice; ++i)
    {
        g->bucket[i] = (graph_node_t*)malloc(sizeof(graph_node_t));
        assert(g->bucket[i]);

        g->bucket[i]->d = i;
        g->bucket[i]->color = WHITE;
        g->bucket[i]->next = NULL;
    }

    return g;
}

void graph_destroy(graph_t *g)
{
    assert(g);

    for (int i = 0; i < g->vertice; ++i)
    {
        graph_node_t *head = g->bucket[i];
        while (head)
        {
            graph_node_t *tmp = head;
            head = head->next;
            free(tmp);
        }
    }
    free(g);
}

void graph_add_edge(graph_t *g, int src, int dst)
{
    assert(g);
    assert(src < g->vertice);
    assert(dst < g->vertice);

    graph_node_t *nd = (graph_node_t*)malloc(sizeof(graph_node_t));
    assert(nd);
    nd->d = dst;
    nd->color = WHITE;
    nd->next = g->bucket[src]->next;
    g->bucket[src]->next = nd;
}

static void _graph_dfs(graph_t *g, int index, int *time)
{
    assert(g);
    assert(time);
    assert(index < g->vertice);

    (*time)++;
    printf("%d ", g->bucket[index]->d);
    g->bucket[index]->color = GRAY;
    g->bucket[index]->dtime = *time;

    graph_node_t *tmp = g->bucket[index]->next;
    while (tmp)
    {
        if (g->bucket[tmp->d]->color == WHITE)
        {
            // 對臨接點進行深度遍歷
            _graph_dfs(g, tmp->d, time);
        }
        tmp = tmp->next;
    }

    g->bucket[index]->color = BLACK;
    (*time)++;
    g->bucket[index]->ftime = *time;
}

// 深度優先遍歷
void graph_dfs(graph_t *g)
{
    assert(g);

    int time = 0;
    for (int i = 0; i < g->vertice; ++i)
    {
        if (g->bucket[i]->color == WHITE)
        {
            _graph_dfs(g, i, &time);
        }
    }
}

// 廣度優先遍歷
void graph_bfs(graph_t *g, int index)
{
    assert(g);
    assert(index < g->vertice);

    queue_t *q = queue_create();

    queue_push(q, g->bucket[index]);
    while (!queue_empty(q))
    {
        graph_node_t *nd = queue_front(q);
        if (g->bucket[nd->d]->color == WHITE)
        {
            printf("%d ", nd->d);
            g->bucket[nd->d]->color = BLACK;

            graph_node_t *head = g->bucket[nd->d]->next;
            while (head)
            {
                // 所有臨接點入隊
                queue_push(q, g->bucket[head->d]);
                head = head->next;
            }
        }
        queue_pop(q);
    }

    queue_destroy(q);
}

int main()
{
    graph_t *g = graph_create(6);

    graph_add_edge(g, 0, 1);
    graph_add_edge(g, 2, 3);
    graph_add_edge(g, 4, 5);
    graph_add_edge(g, 3, 5);
    

    graph_bfs(g, 0);

    graph_destroy(g);

    return 0;
}