本文是針對[資料結構基礎系列(7)：圖]中第1-9課時的實踐專案。
0701 圖結構導學
0702 圖的定義
0703 圖的基本術語
0704 圖的鄰接矩陣儲存結構及演算法
0705 圖的鄰接表儲存結構及演算法
0706 圖的遍歷
0707 非連通圖的遍歷
0708 DFS的應用
0709 BFS的應用

【專案1 - 圖基本演算法庫】

定義圖的鄰接矩陣和鄰接表儲存結構，實現其基本運算，並完成測試。
要求：
1、標頭檔案graph.h中定義相關的資料結構並宣告用於完成基本運算的函式。對應基本運算的函式包括：

void ArrayToMat(int *Arr, int n, MGraph &g); //用普通陣列構造圖的鄰接矩陣
 

void ArrayToList(int *Arr, int n, ALGraph *&); //用普通陣列構造圖的鄰接表
void MatToList(MGraph g,ALGraph *&G);//將鄰接矩陣g轉換成鄰接表G
void ListToMat(ALGraph *G,MGraph &g);//將鄰接表G轉換成鄰接矩陣g
void DispMat(MGraph g);//輸出鄰接矩陣g
void DispAdj(ALGraph *G);//輸出鄰接表G

2、在graph.cpp中實現這些函式
3、用main.cpp中的main函式中完成測試。
[參考解答]

【專案2 - 操作用鄰接表儲存的圖】

　　假設圖G採用鄰接表儲存，分別設計實現以下要求的演算法：
　　（1）輸出出圖G中每個頂點的出度；
　　（2）求出圖G中出度最大的一個頂點，輸出該頂點編號；
　　（3）計算圖G中出度為0的頂點數；
　　（4）判斷圖G中是否存在邊<i,j>。
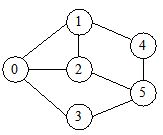
　　利用下圖作為測試用圖，輸出結果。

　　
　　提示：（1）分別設計函式實現演算法；（2）不要全部實現完再測試，而是實現一個，測試一個；（3）請利用圖演算法庫；（４）若將本專案中圖G的儲存結構改為鄰接矩陣，相關操作又如何實現？
參考解答

【專案3 - 圖遍歷演算法實現】

　　實現圖遍歷演算法，分別輸出如下圖結構的深度優先(DFS)遍歷序列和廣度優先遍歷(BFS)序列。

【專案4 - 利用遍歷思想求解圖問題】

　　假設圖G採用鄰接表儲存，分別設計實現以下要求的演算法，要求用區別於示例中的圖進行多次測試，通過觀察輸出值，掌握相關問題的處理方法。
　　（1）設計一個演算法，判斷頂點u到v是否有簡單路徑
　　（2）設計一個演算法輸出圖G中從頂點u到v的一條簡單路徑（設計測試圖時，保證圖G中從頂點u到v至少有一條簡單路徑）。
　　（3）輸出從頂點u到v的所有簡單路徑。
　　（4）輸出圖G中從頂點u到v的長度為s的所有簡單路徑。
　　（5）求圖中通過某頂點k的所有簡單迴路（若存在）
　　[1-5參考解答]
　　（6）求不帶權連通圖G中從頂點u到頂點v的一條最短路徑。
　　（7）求不帶權連通圖G中，距離頂點v最遠的頂點k
　　[6-7參考解答]

【專案5 - 迷宮問題之圖深度優先遍歷解法】

　　設計一個程式，採用深度優先遍歷演算法的思路，解決迷宮問題。
　　（1）建立迷宮對應的圖資料結構，並建立其鄰接表表示。
　　（2）採用深度優先遍歷的思路設計演算法，輸出從入口(1,1)點到出口(M,N)的所有迷宮路徑。
　　[參考解答]

紙上談兵：“知原理”檢驗題目

[參考解答]
1、設圖的鄰接矩陣為，則該圖為__。
A. 有向圖
B. 無向圖
C. 強連通圖
D. 完全圖
2、已知一個圖，如圖1所示，則從頂點a出發按深度優先遍歷則可以得到的一種頂點序列為__。
A. a，b，e，c，d，f
B. a，c，f，e，b，d
C. a，e，b，c，f，d
D. a，e，d，f，c，b
（圖1）
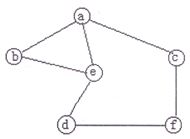
3、畫出圖1的鄰接矩陣和鄰接表儲存的示意圖。

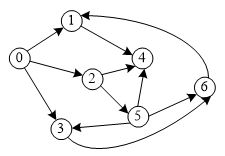
4、已知圖的鄰接矩陣如圖2所示，則從頂點0出發，按深度優先遍歷的頂點序列是_。
（圖2）
A. 0 2 4 3 1 5 6
B. 0 1 3 5 6 4 2
C. 0 4 2 3 1 6 5
D. 0 1 3 4 2 5 6

5、已知圖的鄰接矩陣如圖2，根據演算法，則從頂點0出發，按廣度優先遍歷的結點序列是_
A 0 2 4 3 1 6 5
B. 0 1 3 5 6 4 2
C. 0 1 2 3 4 6 5
D. 0 1 2 3 4 5 6

6、已知圖的鄰接表如圖3所示，根據演算法，則從頂點0出發按深度優先遍歷的結點序列是_
（圖3）
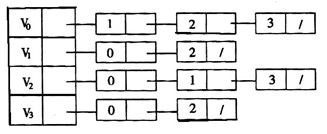
A. 0 1 3 2
B. 0 2 3 1
C. 0 3 2 1
D. 0 1 2 3

7、已知圖的鄰接表如圖3所示，根據演算法，則從頂點0出發按廣度優先遍歷的結點序列是_
A. 0 3 2 1
B. 0 1 2 3
C. 0 1 3 2
D. 0 3 1 2