位置式和增量式PID演算法
一、PID框圖:

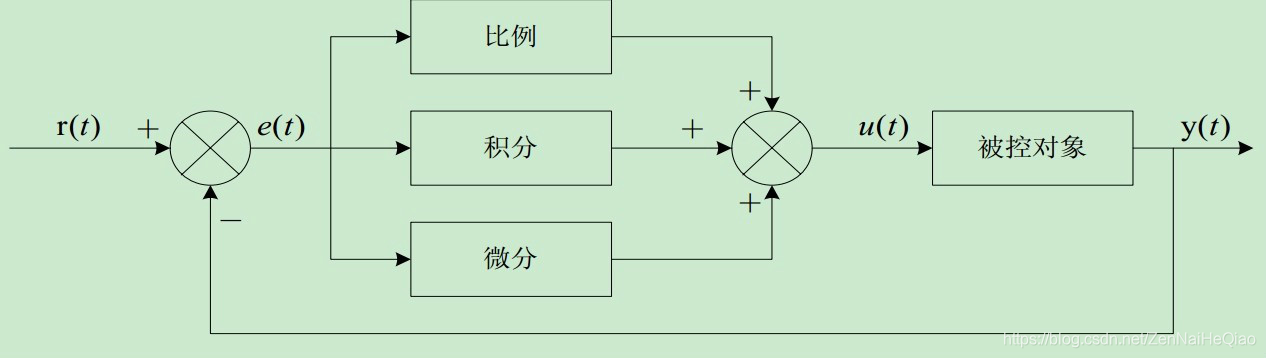
模擬的PID公式
u(t)=Kp[e(t)+Ti1∫0te(t)dt+Tddtde(t)]
將PID公式離散化,推匯出位置式PID公式
u(k)=Kp[ek+Ti1j=0∑kej+TdTek−ek−1]
=Kp∗ek+TiKpj=0∑kej+Kp∗TdTek−ek−1
=Aek+B(j=0∑k−1ej+ek)+C(ek−ek−1)
推匯出增量式PID公式
Δuk=uk−uk−1=Kp[ek−ek−1+TiTek+TdTek−2ek−1+ek−2]
=Kp(1+TiT+TTd)ek−Kp(1+T2Td)ek−1+KpTTdek−2
=Aek+Bek−1+Cek−2
其中,偏差=目標值-反饋值
e
相關推薦
位置式和增量式PID演算法
一、PID框圖:
模擬的PID公式
u
(
位置式和增量式PID控制
PID控制是一個二階線性控制器
定義:通過調整比例、積分和微分三項引數,使得大多數的工業控制系統獲得良好的閉環控制性能。
優點
a. 技術成熟
b. 易被人們熟悉和掌握
c.
深入淺出PID控制演算法(二)————PID演算法離散化和增量式PID演算法原理及Matlab實現
引言
上篇介紹了連續系統的PID演算法,但是計算機控制是一種取樣控制,他只能根據取樣時刻的偏差來計算控制量,因此計算機控制系統中,必須對公式進行離散化,具體就是用求和代替積分,用向後差分來代替微分,使模擬PID離散化為數字形式的差分方程。
準備工
C# 關鍵字explicit(顯示),implicit(隱式),類型的隱式和顯式轉換
tar oid bsp color col 必須 code 類型 顯示
class Program
{
static void Main(string[] args)
{
Adaptee ada = ne
selenium python 顯式和隱式等待方法
http load python exe keys users ive 匿名函數 間隙
1 # -*- coding:utf-8 -*-
2 from selenium import webdriver
3 from selenium.webdriver.commo
(三)使用Intent在活動中穿梭:顯式和隱式Intent
new findview public img 使用 匹配 ted listener style 一、顯式Intent
@Override
protected void onCreate(Bundle savedInstanceState) {
lambda表達式和表達式樹(深入理解c#)
來看 情況下 parameter 成員 表示 3.5 multi ret 委托 1.Lambda形式
1). Lambda表達式最冗長的形式:
(顯式類型的參數列表)=>{語句}
2). 大多數時候,都可以用一個表達式來表示主體,該表達式的值是Lambda的結果,在這
intent的顯式和隱式,更多的intent的用法
用intent實現兩個頁面的跳轉,有連個,一個是顯式,一個是隱式
一、顯式
寫了兩個Activity後,點選按鈕,跳轉到另一個頁面
Intent intent=new Intent(MainActivity.this,OrtherActivty.class);
startActivi
【C#】氣泡排序、隱式和顯式轉換、函式及異常處理
一、普通氣泡排序:
C#中常見的排序方法有:氣泡排序,快速排序,插入排序,選擇排序、堆排序以及歸併排序。雖然還沒學習過,但是也有耳聞,就先把它們先歸類。今天主要講這裡面最常見的氣泡排序。
【概念】
氣泡排序也就是講一組需要排序的數,進行從小到大,或從大到小的排列。計算機
顯式和隱式Intent介紹及intent-filter的action,category,data匹配規則
Intent型別
Intent 分為兩種型別:
顯式 Intent:按名稱(完全限定類名)指定要啟動的元件。 通常,您會在自己的應用中使用顯式 Intent 來啟動元件,這是因為您知道要啟動的 Activity 或服務的類名。例如,啟動新 Activity 以響應使用者
顯式和隱式啟動Activity、Service
Intent尋找目標元件的兩種方式:
顯式Intent:通過指定Intent元件名稱來實現的,它一般用在知道目標元件名稱的前提下,一般是在相同的應用程式內部實現的。隱式Intent:通過Intent Filter來實現的,它一般用在沒有明確指出目標元件名稱的前提下,一般
intent 顯式和隱式
顯式:
最典型的如下`
Intent intent = new Intent(FirstActivity.this,SecondActivity.class);
//在FirstActivity基礎上開啟SecondActivity
startActiv
Android理解:顯式和隱式Intent
Intent是Android初學者比較難理解的一個東西。我這裡以通俗易懂的語言和通俗易懂的程式碼,讓初學者簡單感受一下Intent。intent就是意圖的意思。Intent分兩種:顯式(Explicit intent)和隱式(Implicit intent)。
一、顯式(
Spring程式設計式和宣告式事務例項講解
開發十年,就只剩下這套架構體系了!
>>>
Python-lambda表達式和推導式
pytho ssi 變量 sorted red baidu argument 列表推導 參數傳遞 lambda表達式和推導式,可實現使用一行語句完成功能開發的效果,減少代碼量。
1.lambda表達式
匿名函數,即沒有名字的函數
1.1基本語法:
lambda ar
箭頭函數表達式和聲名式函數表達式的區別以及 Function.prototype的bind, apply,call方法
不知道 -c 兩個 eva 一個 true ice 函數表 prototype 箭頭函數不能用做構造函數
箭頭函數沒有arguments參數
箭頭函數沒有自己的this,是從作用域鏈上取this,是與箭頭函數定義的位置有關的,與執行時誰調用無關,所以用call,appl
增量式線上學習:對最先進的演算法進行回顧和比較
翻譯論文:Incremental On-line Learning:A Review and Comparison of State of the Art Algorithms
作者:Viktor Losing, Barbara Hammer, Heiko W
【資料結構週週練】014 利用棧和非遞迴演算法求鏈式儲存的二叉樹是否為完全二叉樹
一、前言
首先,明天是個很重要的節日,以後我也會過這個節日,在這裡,提前祝所有程式猿們,猿猴節快樂,哦不,是1024程式設計師節快樂。
今天要給大家分享的演算法是判斷二叉樹是否為完全二叉樹,相信大家對完全二叉樹的概念並不陌生,如果是順序儲存就會很方便,那鏈式儲存怎麼判斷呢,我的做法是:若
增量式編碼器和絕對式編碼器,ABI訊號和UVW訊號、編碼器PWM訊號
一、編碼器的分類
根據檢測原理,編碼器可分為光學式、磁式、感應式和電容式,根據其刻度方法及訊號輸出形式,可分為增量式、絕對式以及混合式三種。
1、增量式編碼器 增量式編碼器是直接利用光電轉換原理輸出三組方波脈衝A、B和Z相;A、B兩組脈衝相位差90。,從而可方便的判斷出旋轉方向
爬蟲的增量式抓取和資料更新
爬蟲的增量式抓取和資料更新
頁面爬的多了,量上去了之後,就會遇到其他的問題,其實不管做什麼技術量大了都會有問題。一般情況下,我認為解決"大量"問題的思路有兩個:一種是著力於優化系統的能力,讓原本只能一分鐘處理100條的系統提升到一分鐘1000條之類的,在我看來並行、分散式、叢
位置式和增量式PID演算法
一、PID框圖: 模擬的PID公式 u (
位置式和增量式PID控制
PID控制是一個二階線性控制器 定義:通過調整比例、積分和微分三項引數,使得大多數的工業控制系統獲得良好的閉環控制性能。 優點 a. 技術成熟 b. 易被人們熟悉和掌握 c.
深入淺出PID控制演算法(二)————PID演算法離散化和增量式PID演算法原理及Matlab實現
引言 上篇介紹了連續系統的PID演算法,但是計算機控制是一種取樣控制,他只能根據取樣時刻的偏差來計算控制量,因此計算機控制系統中,必須對公式進行離散化,具體就是用求和代替積分,用向後差分來代替微分,使模擬PID離散化為數字形式的差分方程。 準備工
C# 關鍵字explicit(顯示),implicit(隱式),類型的隱式和顯式轉換
tar oid bsp color col 必須 code 類型 顯示 class Program { static void Main(string[] args) { Adaptee ada = ne
selenium python 顯式和隱式等待方法
http load python exe keys users ive 匿名函數 間隙 1 # -*- coding:utf-8 -*- 2 from selenium import webdriver 3 from selenium.webdriver.commo
(三)使用Intent在活動中穿梭:顯式和隱式Intent
new findview public img 使用 匹配 ted listener style 一、顯式Intent @Override protected void onCreate(Bundle savedInstanceState) {
lambda表達式和表達式樹(深入理解c#)
來看 情況下 parameter 成員 表示 3.5 multi ret 委托 1.Lambda形式 1). Lambda表達式最冗長的形式: (顯式類型的參數列表)=>{語句} 2). 大多數時候,都可以用一個表達式來表示主體,該表達式的值是Lambda的結果,在這
intent的顯式和隱式,更多的intent的用法
用intent實現兩個頁面的跳轉,有連個,一個是顯式,一個是隱式 一、顯式 寫了兩個Activity後,點選按鈕,跳轉到另一個頁面 Intent intent=new Intent(MainActivity.this,OrtherActivty.class); startActivi
【C#】氣泡排序、隱式和顯式轉換、函式及異常處理
一、普通氣泡排序: C#中常見的排序方法有:氣泡排序,快速排序,插入排序,選擇排序、堆排序以及歸併排序。雖然還沒學習過,但是也有耳聞,就先把它們先歸類。今天主要講這裡面最常見的氣泡排序。 【概念】 氣泡排序也就是講一組需要排序的數,進行從小到大,或從大到小的排列。計算機
顯式和隱式Intent介紹及intent-filter的action,category,data匹配規則
Intent型別 Intent 分為兩種型別: 顯式 Intent:按名稱(完全限定類名)指定要啟動的元件。 通常,您會在自己的應用中使用顯式 Intent 來啟動元件,這是因為您知道要啟動的 Activity 或服務的類名。例如,啟動新 Activity 以響應使用者
顯式和隱式啟動Activity、Service
Intent尋找目標元件的兩種方式: 顯式Intent:通過指定Intent元件名稱來實現的,它一般用在知道目標元件名稱的前提下,一般是在相同的應用程式內部實現的。隱式Intent:通過Intent Filter來實現的,它一般用在沒有明確指出目標元件名稱的前提下,一般
intent 顯式和隱式
顯式: 最典型的如下` Intent intent = new Intent(FirstActivity.this,SecondActivity.class); //在FirstActivity基礎上開啟SecondActivity startActiv
Android理解:顯式和隱式Intent
Intent是Android初學者比較難理解的一個東西。我這裡以通俗易懂的語言和通俗易懂的程式碼,讓初學者簡單感受一下Intent。intent就是意圖的意思。Intent分兩種:顯式(Explicit intent)和隱式(Implicit intent)。 一、顯式(
Spring程式設計式和宣告式事務例項講解
開發十年,就只剩下這套架構體系了! >>>
Python-lambda表達式和推導式
pytho ssi 變量 sorted red baidu argument 列表推導 參數傳遞 lambda表達式和推導式,可實現使用一行語句完成功能開發的效果,減少代碼量。 1.lambda表達式 匿名函數,即沒有名字的函數 1.1基本語法: lambda ar
箭頭函數表達式和聲名式函數表達式的區別以及 Function.prototype的bind, apply,call方法
不知道 -c 兩個 eva 一個 true ice 函數表 prototype 箭頭函數不能用做構造函數 箭頭函數沒有arguments參數 箭頭函數沒有自己的this,是從作用域鏈上取this,是與箭頭函數定義的位置有關的,與執行時誰調用無關,所以用call,appl
增量式線上學習:對最先進的演算法進行回顧和比較
翻譯論文:Incremental On-line Learning:A Review and Comparison of State of the Art Algorithms 作者:Viktor Losing, Barbara Hammer, Heiko W
【資料結構週週練】014 利用棧和非遞迴演算法求鏈式儲存的二叉樹是否為完全二叉樹
一、前言 首先,明天是個很重要的節日,以後我也會過這個節日,在這裡,提前祝所有程式猿們,猿猴節快樂,哦不,是1024程式設計師節快樂。 今天要給大家分享的演算法是判斷二叉樹是否為完全二叉樹,相信大家對完全二叉樹的概念並不陌生,如果是順序儲存就會很方便,那鏈式儲存怎麼判斷呢,我的做法是:若
增量式編碼器和絕對式編碼器,ABI訊號和UVW訊號、編碼器PWM訊號
一、編碼器的分類 根據檢測原理,編碼器可分為光學式、磁式、感應式和電容式,根據其刻度方法及訊號輸出形式,可分為增量式、絕對式以及混合式三種。 1、增量式編碼器 增量式編碼器是直接利用光電轉換原理輸出三組方波脈衝A、B和Z相;A、B兩組脈衝相位差90。,從而可方便的判斷出旋轉方向
爬蟲的增量式抓取和資料更新
爬蟲的增量式抓取和資料更新 頁面爬的多了,量上去了之後,就會遇到其他的問題,其實不管做什麼技術量大了都會有問題。一般情況下,我認為解決"大量"問題的思路有兩個:一種是著力於優化系統的能力,讓原本只能一分鐘處理100條的系統提升到一分鐘1000條之類的,在我看來並行、分散式、叢
