洛谷 P3159(BZOJ 2668)[CQOI2012]交換棋子
阿新 • • 發佈:2018-11-16
有一個\(n\)行\(m\)列的黑白棋盤,你每次可以交換兩個相鄰格子(相鄰是指有公共邊或公共頂點)中的棋子,最終達到目標狀態。要求第\(i\)行第\(j\)列的格子只能參與\(m[i][j]\)次交換。
輸入格式:
第一行包含兩個整數\(n,m(1<=n, m<=20)\)。
以下\(n\)行為初始狀態,每行為一個包含\(m\)個字元的\(01\)串,其中\(0\)表示黑色棋子,\(1\)表示白色棋子。
以下\(n\)行為目標狀態,格式同初始狀態。
以下\(n\)行每行為一個包含\(m\)個\(0-9\)數字的字串,表示每個格子參與交換的次數上限。
輸出格式:
輸出僅一行,為最小交換總次數。如果無解,輸出\(-1\)
輸入樣例#1:
3 3
110
000
001
000
110
100
222
222
222輸出樣例#1:
4最近一直在學習網路流。寫到這個題目的時候,第一反應是:“這怎麼可能是網路流呢?”用了一個下午寫出來這道題後,感覺其思路實在妙極。
本題解力求讓像我一樣初學網路流(初學OI)的人能夠看懂,如果還存在疑惑的話歡迎聯絡我哦~
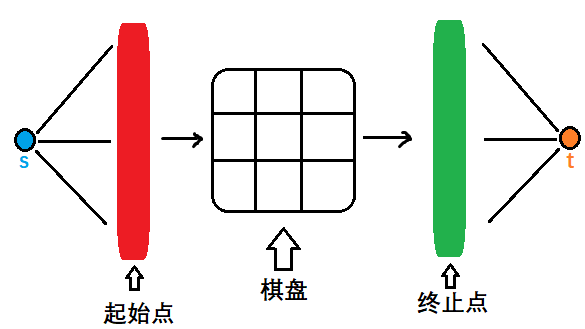
看這個題目,很容易想到:可以記錄黑色棋子的起始和終結位置,想辦法去讓棋子從起始位置走到終止位置,一一匹配。棋子在棋盤上走,走的過程中,棋子受到必須成功匹配(最大流)和在此基礎上費用最小的約束條件。這樣考慮的話,跑費用流自然是再合適不過了。如下圖所示:
進一步考慮會發現,棋子的交換可以被視為在棋盤上的座標移動。想要連通起始點和終止點,只需要在二者之間建立棋盤的八連通圖,讓棋子在對應位置上進出棋盤即可。
但是現在,有一個關鍵的問題:起始點和終止點作交換的時候, 消耗流量是\(1\),但是對於中間節點,消耗流量卻都應該是\(2\)。如果單純的考慮把一個點拆分成一條邊的話,無法處理這種邊界情況,事情就變得相對比較麻煩。
迴歸題目來考慮,題目要求是交換,那麼交換就有交換進來和交換出去這兩種交換方法。根據這個給我們的靈感,我們可以考慮把一個點拆成\(3\)個:\(inn\),\(mid\)和\(out\),把原本的最大訪問量均分在兩端上,而把每次的進出流量視為\(1\)。這樣同時又解決了進出棋盤的問題:直接在\(mid\)處進入棋盤就不用考慮其他麻煩的事情了。
那麼流量均分的想法是否正確呢?基本上是對的。但是,現在我們有了\(inn\)
所以這裡又牽涉到了這一點邊界的處理問題。如果棋盤開始和結束都有或都沒有該棋子,那麼我們對可用點權\(maxf\)取\(1/2\)。否則的話,分別考慮進入和出去的情況:

可以看到,進入時的\(mid\)->\(out\),出去時的\(inn\)->\(mid\)會有一條耗流為\(1\)的邊,我們考慮如果這個點不是既進又出節點,就給其存在\(1\)耗流邊的一部分嘗試多分配一點"零頭"流量(即偶數分配為\(n/2\)或\((n+1)/2\)都一樣,而奇數則分配為\(n/2\):\((n+1)/2\)。)
為了便於各位理清思路,這裡本人貼一下建圖流程:
- 初始點->\(S\) \(f=1\) \(w=0\)
- 最終點<-\(T\) \(f=1\) \(w=0\)
- 初始點->對應座標的\(mid\)節點 \(f=1\) \(w=0\)
- 對應座標的\(mid\)節點->終止點 \(f=1\) \(w=0\)
- 棋盤內部的八連通:(\(out\)->\(in\)) \(f=INF\) \(w=1\)
- \(inn\)->\(mid\)和\(mid\)->\(out\):\(w=1\),根據情況確認選擇 \(f=maxf/2\) 或者 \(f=(maxf+1)/2\)
至此,問題得以完美解決。程式碼冗長求輕噴。
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 2010
#define MAXM 64010
#define INF 0x3f3f3f3f
#define fpop(x) x.front();x.pop()
using namespace std;
int pre_node[MAXN],pre_edge[MAXN];
char ch,mp_bg[25][25],mp_ed[25][25];
int n,m,cnt=-1,dis[MAXN],vis[MAXN],flow[MAXN],head[MAXN],maxf[25][25];
struct edge{
int nxt,to,w,f;
}e[MAXM];
inline int _bg(int x,int y){return n*m*0+(x-1)*m+y;}//起始點[x,y]的編號
inline int _ed(int x,int y){return n*m*1+(x-1)*m+y;}//目標點[x,y]的編號
inline int _inn(int x,int y){return n*m*2+(x-1)*m+y;}//棋盤[x,y]的Inn點編號
inline int _mid(int x,int y){return n*m*3+(x-1)*m+y;}//棋盤[x,y]的mid點標號
inline int _out(int x,int y){return n*m*4+(x-1)*m+y;}//棋盤[x,y]的Out點編號
inline bool in_map(int x,int y){
return 1<=x && x<=n && 1<=y && y<=m;
}//判斷是否越界
inline void add_edge(int from,int to,int flw,int val){
e[++cnt].nxt=head[from];
e[cnt].to=to;
e[cnt].f=flw;
e[cnt].w=val;
head[from]=cnt;
}
queue<int>que;
inline bool spfa(int s,int t){
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
memset(flow,0x3f,sizeof(flow));
que.push(s); vis[s]=true; dis[s]=0;
while(!que.empty()){
int u=fpop(que);
for(int i=head[u];~i;i=e[i].nxt){
int v=e[i].to;
if(dis[v]>dis[u]+e[i].w && e[i].f){
dis[v]=dis[u]+e[i].w;
flow[v]=min(flow[u],e[i].f);
pre_node[v]=u;
pre_edge[v]=i;
vis[v]=true;que.push(v);
}
}
}
return dis[t]!=INF;
}
int mv[8][2]={{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}};
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf(" %c",&mp_bg[i][j]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf(" %c",&mp_ed[i][j]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
scanf(" %c",&ch);
maxf[i][j]=ch-'0';
//最大經過次數
}
}
//輸入起始態和目標態棋盤
int s=0,t=n*m*5+1;
int cnt_1=0,cnt_2=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(mp_bg[i][j]==mp_ed[i][j]){
add_edge(_inn(i,j),_mid(i,j),maxf[i][j]/2,0);
add_edge(_mid(i,j),_inn(i,j),000000000000,0);
add_edge(_mid(i,j),_out(i,j),maxf[i][j]/2,0);
add_edge(_out(i,j),_mid(i,j),000000000000,0);
}else{
if(mp_bg[i][j]=='1'){
add_edge(_inn(i,j),_mid(i,j),(maxf[i][j]+0)/2,0);
add_edge(_mid(i,j),_inn(i,j),000000000000,0);
add_edge(_mid(i,j),_out(i,j),(maxf[i][j]+1)/2,0);
add_edge(_out(i,j),_mid(i,j),000000000000,0);
}
if(mp_ed[i][j]=='1'){
add_edge(_inn(i,j),_mid(i,j),(maxf[i][j]+1)/2,0);
add_edge(_mid(i,j),_inn(i,j),000000000000,0);
add_edge(_mid(i,j),_out(i,j),(maxf[i][j]+0)/2,0);
add_edge(_out(i,j),_mid(i,j),000000000000,0);
}
}
if(mp_bg[i][j]=='1'){
++cnt_1;
//連線源點到初始點 f=1 w=0;
add_edge(s,_bg(i,j),1,0);
add_edge(_bg(i,j),s,0,0);
//連線起始點到棋盤
add_edge(_bg(i,j),_mid(i,j),1,0);
add_edge(_mid(i,j),_bg(i,j),0,0);
}
if(mp_ed[i][j]=='1'){
++cnt_2;
//連線終結點到匯點 f=1 w=0;
add_edge(_ed(i,j),t,1,0);
add_edge(t,_ed(i,j),0,0);
//連線棋盤到終結點
add_edge(_mid(i,j),_ed(i,j),1,0);
add_edge(_ed(i,j),_mid(i,j),0,0);
}
//棋盤的八連通邊 f=INF w=1;
for(int k=0;k<8;++k){
int ni=i+mv[k][0];
int nj=j+mv[k][1];
if(in_map(ni,nj)){
//從點[i,j]的out連線點[ni,nj]的inn
add_edge(_out(i,j),_inn(ni,nj),INF,+1);
add_edge(_inn(ni,nj),_out(i,j),000,-1);
}
}
}
}
//棋子數變動->No solution
if(cnt_1!=cnt_2){
puts("-1");
return 0;
}
//然後跑費用流
int max_flow=0,min_cost=0;
while(spfa(s,t)){
max_flow+=flow[t];
min_cost+=flow[t]*dis[t];
int u=t;
while(u!=s){
e[pre_edge[u]^0].f-=flow[t];
e[pre_edge[u]^1].f+=flow[t];
u=pre_node[u];
}
}
if(max_flow!=cnt_1){
puts("-1");
return 0;
}
printf("%d\n",min_cost);
}