題目描述

在一個遙遠的國度，一側是風景秀美的湖泊，另一側則是漫無邊際的沙漠。該國的行政區劃十分特殊，剛好構成一個NNN 行×M \times M×M 列的矩形，如上圖所示，其中每個格子都代表一座城市，每座城市都有一個海拔高度。

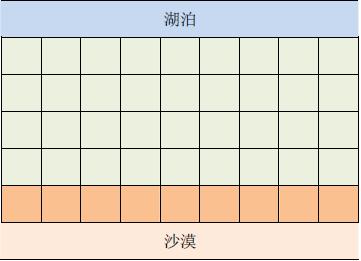
為了使居民們都盡可能飲用到清澈的湖水，現在要在某些城市建造水利設施。水利設施有兩種，分別為蓄水廠和輸水站。蓄水廠的功能是利用水泵將湖泊中的水抽取到所在城市的蓄水池中。

因此，只有與湖泊毗鄰的第111 行的城市可以建造蓄水廠。而輸水站的功能則是通過輸水管線利用高度落差，將湖水從高處向低處輸送。故一座城市能建造輸水站的前提，是存在比它海拔更高且擁有公共邊的相鄰城市，已經建有水利設施。由於第NNN 行的城市靠近沙漠，是該國的幹旱區，所以要求其中的每座城市都建有水利設施。那麽，這個要求能否滿足呢？如果能，請計算最少建造幾個蓄水廠；如果不能，求幹旱區中不可能建有水利設施的城市數目。

輸入輸出格式

每行兩個數，之間用一個空格隔開。輸入的第一行是兩個正整數N,MN,MN,M，表示矩形的規模。接下來NNN 行，每行MMM 個正整數，依次代表每座城市的海拔高度。

兩行。如果能滿足要求，輸出的第一行是整數111，第二行是一個整數，代表最少建造幾個蓄水廠；如果不能滿足要求，輸出的第一行是整數000，第二行是一個整數，代表有幾座幹旱區中的城市不可能建有水利設施。

輸入輸出樣例

2 5
9 1 5 4 3
8 7 6 1 2

1
1

3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2

1
3

說明

【樣例1 說明】

只需要在海拔為999 的那座城市中建造蓄水廠，即可滿足要求。

【樣例2 說明】

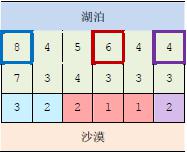
上圖中，在33 3個粗線框出的城市中建造蓄水廠，可以滿足要求。以這33 3個蓄水廠為源頭在幹旱區中建造的輸水站分別用3 種顏色標出。當然，建造方法可能不唯一。

【數據範圍】

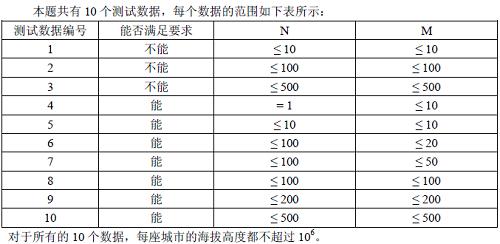
首先需要知道最上面一層能夠往沙漠地區輸送的範圍為連續的一段（可以用反證法

所以只需dfs找到每一個輸水源頭的輸送範圍再進行判斷

 1 #include<bits/stdc++.h>
 2 #define inf 0x3f3f3f3f
 3
 
 using namespace std;
 4 
 5 inline int read(){
 6     int x=0,f=1;char ch=getchar();
 7     while(ch>‘9‘||ch<‘0‘) {if(ch==‘-‘) f=-1;ch=getchar();}
 8     while(ch>=‘0‘&&ch<=‘9‘) {x=x*10+ch-‘0‘;ch=getchar();}
 9     return f*x;
10 }
11 
12 struct edge{
13     int l,r;
14 }qj[501][501];
15 
16 bool bj[501][501];
17 
18 int mp[501][501],dirx[]={0,-1,1,0,0},diry[]={0,0,0,-1,1},n,m;
19 
20 void dfs(int x,int y){
21     bj[x][y]=1;
22     for(int i=1;i<=4;i++){
23         int nx=x+dirx[i],ny=y+diry[i];
24         if(nx>n||nx<1||ny>m||ny<1) continue;
25         if(mp[nx][ny]>=mp[x][y]) continue;
26         if(!bj[nx][ny]) dfs(nx,ny);
27         qj[x][y].l=min(qj[x][y].l,qj[nx][ny].l);
28         qj[x][y].r=max(qj[x][y].r,qj[nx][ny].r);
29     }
30 }
31 
32 int main(){
33     n=read(),m=read();
34     for(int i=1;i<=n;i++)
35         for(int j=1;j<=m;j++)
36         mp[i][j]=read();
37     for(int i=1;i<n;i++) 
38         for(int j=1;j<=m;j++) qj[i][j].l=inf,qj[i][j].r=0;
39     for(int i=1;i<=m;i++) qj[n][i].l=qj[n][i].r=i;
40     for(int i=1;i<=m;i++)  if(!bj[1][i]) dfs(1,i);
41     int cnt=0;bool ok=1;
42     for(int i=1;i<=m;i++){
43         if(bj[n][i]) cnt++;else ok=0;
44     }
45     if(!ok){
46         printf("0\n");printf("%d\n",m-cnt);return 0;
47     }
48     int left=1;cnt=0;
49     while(left<=m){
50         int maxr=0;
51         for(int i=1;i<=m;i++) if(qj[1][i].l<=left) maxr=max(maxr,qj[1][i].r);
52         cnt++;left=maxr+1;
53     }
54     printf("1\n%d\n",cnt);
55     /*for(int i=1;i<=m;i++){
56         printf("%d %d\n",qj[1][i].l,qj[1][i].r); 
57     }*/
58     return 0;
59 }

洛谷p1514（dfs+貪心）