分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow

也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！

                【專案 ：窮舉法解決組合問題】（自選兩題完成，其他的想一想即可。當然，全做完收效更好）

先閱讀例題，領會窮舉法（意為“窮盡式列舉”，也稱列舉）的思想，然後自行選題進行解決，掌握這種程式設計的一般方法。

例題：小明有五本新書，要借給A，B，C三位小朋友，若每人每次只能借一本，則可以有多少種不同的借法？

問題分析與演算法設計：本問題實際上是一個排列問題，即求從5箇中取3個進行排列的方法的總數。首先對五本書從1至5進行編號，然後使用窮舉的方法。假設三個人分別借這五本書中的一本，當三個人所借的書的編號都不相同時，就是滿足題意的一種借閱方法。

下面是程式及其註釋，要注意利用三重迴圈“窮舉”：

#include <iostream> using namespace std;int main(){ int a,b,c,count=0; cout<<"小明借書給三位小朋友書的方案有："
 
<<endl; for(a=1;a<=5;a++)   //窮舉a借5本書中的1本的全部情況  for(b=1;b<=5;b++)  //窮舉b借5本書中的一本的全部情況   for(c=1;c<=5;c++) //窮舉c借5本書中的1本的全部情況    if(a!=b&&c!=a&&c!=b) //判斷三個人借的書是否不同，(a-b)*(b-c)*(c-a)!=0更好    {     ++count;     cout
 
<<count<<": "<<a<<", "<<b<<", "<<c<<endl;//輸出方案    } return 0;}

任務：利用窮舉的方法解決下面的問題（選做一道即算完成任務，其他可以抽時間自由安排，多做會使你更聰明。）

（1）百錢百雞問題：中國古代數學家張丘建在他的《算經》中提出了著名的“百錢買百雞問題”：雞翁一，值錢五，雞母一，值錢三，雞雛三，值錢一，百錢買百雞，問翁、母、雛各幾何？

提示：設雞翁、雞母、雞雛的個數分別為x,y,z，題意給定共100錢要買百雞，若全買公雞最多買20只，顯然x的值在0~20之間；同理，y的取值範圍在0~33之間，可得到下面的不定方程：

5x+3y+z/3=100

x+y+z=100

所以此問題可歸結為求這個不定方程的整數解。

由程式設計實現不定方程的求解與手工計算不同。在分析確定方程中未知數變化範圍的前提下，可通過對未知數可變範圍的窮舉，驗證方程在什麼情況下成立，從而得到相應的解。

引申：這類求解不定方程的實現，各層迴圈的控制變數直接與方程未知數有關，且採用對未知數的取值範圍上窮舉和組合的方法來複蓋可能得到的全部各組解。如果要採取技巧，往往是根據題意，更合理地設定迴圈控制條件來減少這種窮舉和組合的次數，提高程式的執行效率，需要具體問題具體分析。

參考解答：

#include <iostream>using namespace std;int main(){ int x,y,z;       //定義資料型別為整型，買雞和買烤雞不是一個概念 for(x=0;x<=20;++x)  for(y=0;y<=33;++y)  //窮舉中。。。。   for(z=0;z<=300;++z)    if(5*x+3*y+z/3==100 && x+y+z==100 && z%3==0)    {     cout<<"雞翁"<<x<<"只，雞母"<<y<<"只，雞雛"<<z<<"只。"<<endl;    } return 0;}

執行結果：

改進一：

#include <iostream>using namespace std;int main(){ int x,y,z;       //定義資料型別為整型，防止出現買烤雞情況的出現 for(x=0;x<=20;++x)  for(y=0;y<=33;++y)     for(z=0;z<=300;z+=3)  //既然z要整除3，每次自加3去保證，少了迴圈，也少了判斷    if(5*x+3*y+z/3==100 && x+y+z==100)    {     cout<<"雞翁"<<x<<"只，雞母"<<y<<"只，雞雛"<<z<<"只。"<<endl;    } return 0;}

改進二：

#include <iostream>using namespace std;int main(){ int x,y,z;        for(x=0;x<=20;++x)  for(y=0;y<=33;++y)    {   z=100-x-y;   //雞雛數就此確定，何須再去試探——窮舉只是笨辦法，人可以讓計算機輕鬆些   if(5*x+3*y+z/3==100&&z%3==0)     cout<<"雞翁"<<x<<"只，雞母"<<y<<"只，雞雛"<<z<<"只。"<<endl;  } return 0;}

（2）換分幣：用一元人民幣兌換成1分、2分和5分硬幣，有多少種不同的兌換方法？請輸出所有可能的方案。

提示：根據題意設i,j,k分別為兌換的1分、2分、5分硬幣的枚數，則i,j,k的值應滿足：i+j*2+k*5=100，根據取值範圍構造迴圈解題即可。

參考解答：

提示：根據題意設i,j,k分別為兌換的1分、2分、5分硬幣的枚數，則i,j,k的值應滿足：i+j*2+k*5=100，根據取值範圍構造迴圈解題即可。

#include<iostream>using namespace std;int main(){ int i,j,k,count=0; for(i=0;i<=100;i++)  for(j=0;j<=50;j++)   for(k=0;k<=20;k++)   {    if(i+j*2+k*5==100)    {     ++count;     cout<<"第"<<count<<"種";     cout<<" "<<"1分錢:"<<i;     cout<<" "<<"2分錢:"<<j;     cout<<" "<<"5分錢:"<<k<<endl;     if(count%50==0)   //每輸出50個方案暫停一次     {      cout<<"按任意鍵繼續輸出（找不到任意鍵打客服電話問詢）……"<<endl;      getchar();     }    }   } return 0;}

執行結果：

（3）年齡幾何：張三、李四、王五、劉六的年齡成一等差數列，他們四人的年齡相加是26，相乘是880，求以他們的年齡為前4項的等差數列的前20項。

提示：設數列的首項為n，項差為a，則前4項之和為n+(n+a)+(n+a+a)+(n+a+a+a)=4*n+6*a"，前4 項之積為n*(n+a)*(n+a+a)*(n+a+a+a)。同時有1<=a<=4和1<=n<=6。可採用窮舉法求出此數列。

參考解答：

#include<iostream>  using namespace std;  int main()  {      int a,n,i,s;      for(a=1;a<=4;a++)  //列舉        for(n=1;n<=6;n++)     if(n*4+a*6==26 && n*(n+a)*(n+a+a)*(n+a+a+a)==880)     {    cout<<n;  //輸出第1個    for(i=1;i<20;i++)      {       s=n+a*i;       cout<<","<<s;  //後面的19個都和前一個用逗號分隔輸出    }      cout<<endl;     } return 0;  }  

執行結果：

（4）三色球問題：若一個口袋中放有12個球，其中有3個紅的。3個白的和6個黒的，問從中任取8個共有多少種不同的顏色搭配？

提示：設任取的紅球個數為i，白球個數為j，則黒球個數為8-i-j，根據題意紅球和白球個數的取值範圍是0~3，在紅球和白球個數確定的條件下，黒球個數取值應為8-i-j<=6。

參考解答：

#include<iostream>using namespace std;int main (){ int red,white,black; cout<<"不同的顏色搭配有:"<<endl; for(red=0;red<=3;red++)  for(white=0;white<=3;white++)  {   black=8-red-white;   if(black<=6)   {    cout<<"紅球:"<<red<<","<<"白球:"<<white<<","<<"黑球:"<<black<<endl;   }  } return 0;}

執行結果：

（5）委派任務：某偵察隊接到一項緊急任務，要求在A、B、C、D、E、F六個隊員中儘可能多地挑若干人，但有以下限制條件：

l A和B兩人中至少去一人；

l A和D不能一起去；

l A、E和F三人中要派兩人去；

l B和C都去或都不去；

l C和D兩人中去一個；

l 若D不去，則E也不去。

問應當讓哪幾個人去？

提示：用a、b、c、d、e、f六個變量表示六個人是否去執行任務的狀態，變數的值為1，則表示該人去；變數的值為0，則表示該人不參加執行任務，根據題意可寫出表示式：

l a+b>1     //A和B兩人中至少去一人；

l (a+d)!=2      //A和D不能一起去；

l a+e+f==2     // A、E、F三人中要派兩人去；

l b+c==0或b+c==2     // B和C都去或都不去；

l c+d==1      //C和D兩人中去一個；

l d+e==0或d==1       //若D不去，則E也不去(都不去；或D去E隨便)。

上述各表示式之間的關係為“與”關係。窮舉每個人去或不去的各種可能情況，代入上述表示式中進行推理運算，使上述表示式均為“真”的情況就是正確的結果。

參考解答：

#include<iostream>  using namespace std;  int main(){ int a,b,c,d,e,f; for(a=1;a>=0;a--) //窮舉每個人是否去的所有情況  for(b=1;b>=0;b--) //1:去 0:不去   for(c=1;c>=0;c--)    for(d=1;d>=0;d--)     for(e=1;e>=0;e--)      for(f=1;f>=0;f--)       if(a+b>=1&&a+d!=2&&a+e+f==2&&(b+c==0||b+c==2)&&c+d==1&&(d+e==0||d==1))       {        cout<<"A "<<(a?"":"不")<<"去。"<<endl;        cout<<"B "<<(b?"":"不")<<"去。"<<endl;        cout<<"C "<<(c?"":"不")<<"去。"<<endl;        cout<<"D "<<(d?"":"不")<<"去。"<<endl;        cout<<"E "<<(e?"":"不")<<"去。"<<endl;        cout<<"F "<<(f?"":"不")<<"去。"<<endl;       } return 0;}

執行結果：

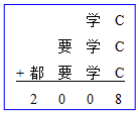
（6）在下面的加法算式中，不同的符號代表不同的數字，相同的符號代表相同的數字。請設計程式求出"都、要、學、C"4個符號分別代表的數字。

提示：讓計算機解奧數題。窮舉"都、要、學、C"4個符號分別代表的數字（從0到9），然後進行組合，如果組合起來符合規則（不同的符號代表不同的數字，相同的符號代表相同的數字，且使等式成立），則為正解。

參考解答：未優化前的程式碼 

#include <iostream>  using namespace std;  int main()  {  int dou,yao,xue,c,s;//變數這樣取，比用i,j,p,q之類的要清晰得多 for(dou=1;dou<3;dou++)  for(yao=0;yao<10;yao++)   for(xue=0;xue<10;xue++)    for(c=0;c<10;c++)     if((dou-yao)*(dou-xue)*(dou-c)*(yao-xue)*(yao-c)*(xue-c)!=0)//一個技巧：表示兩兩不同可以這樣做     {      s=4*c+3*xue*10+2*yao*100+dou*1000;      if(2008==s)        cout<<"都："<<dou<<" 要："<<yao<<" 學："<<xue<<" C："<<c<<endl;     } return 0;}  

執行結果

效率更高的解法 

#include <iostream>  using namespace std;  int main()  {  int dou,yao,xue,c,s; for(dou=1;dou<3;dou++)  for(yao=0;yao<10;yao++)  {   if(dou==yao) continue;//“都”和“要”的取值如果相同了，將不再考慮另外兩字的取值，效果可觀   for(xue=0;xue<10;xue++)   {    if(xue==yao||xue==dou) continue;  //理由同上    for(c=0;c<10;c++)     if((dou-c)*(yao-c)*(xue-c)!=0)     {      s=4*c+3*xue*10+2*yao*100+dou*1000;      if(2008==s)        cout<<"都："<<dou<<" 要："<<yao<<" 學："<<xue<<" C："<<c<<endl;     }   }  } return 0;}

視訊講解：http://www.tudou.com/programs/view/InJLdkTDKSQ/

（7）警察局抓住了A、B、C、D四名盜竊嫌疑犯，其中只有一人是小偷。在審問時，A說：“我不是小偷”；B說：“C是小偷”；C說：“小偷肯定是D”；D說：“C在冤枉好人”。現在已經知道這四人中有三人說的是真話，一人說的是假話。請問到底誰是小偷？

提示：設4個變數a,b,c,d，為0時表示不是小偷，為1時表示是小偷，用四重迴圈窮舉a,b,c,d可能的取值的組合，對每一種組合判斷其是否符合題目中給出的約束。最後結論：C是小偷。

參考解答：

#include<iostream>  using namespace std;  int main(){ int a,b,c,d; for(a=1;a>=0;a--) //窮舉每個人是否是小偷的所有情況  for(b=1;b>=0;b--) //1:是小偷 0:不是   for(c=1;c>=0;c--)    for(d=1;d>=0;d--)     if((a==0)+(c==1)+(d==1)+(d==0)==3&&a+b+c+d==1) //4人的說法中有3個真的，且只有一個小偷      {      cout<<"A "<<(a?"":"不")<<"是。"<<endl;      cout<<"B "<<(b?"":"不")<<"是。"<<endl;      cout<<"C "<<(c?"":"不")<<"是。"<<endl;      cout<<"D "<<(d?"":"不")<<"是。"<<endl;     } return 0;}

下面一個程式的寫法中，注意“4人的說法中有3個真的”(即if語句部分)的寫法，理解了，就又是一個提高！要點，例：

當a為0時!a為1,a為1時!a為0，等同於a==0及a!=1的值，即　　　

a	!a	a==0	a!=1
0	1	1	1
1	0	0	0

#include<iostream>  using namespace std;  int main(){ int a,b,c,d; for(a=1;a>=0;a--) //窮舉每個人是否是小偷的所有情況  for(b=1;b>=0;b--) //1:是小偷 0:不是   for(c=1;c>=0;c--)    for(d=1;d>=0;d--)     if((!a)+(c)+(d)+(!d)==3&&a+b+c+d==1) //!a與a==0或a!=1完全等價，其他同      {      cout<<"A "<<(a?"":"不")<<"是。"<<endl;      cout<<"B "<<(b?"":"不")<<"是。"<<endl;      cout<<"C "<<(c?"":"不")<<"是。"<<endl;      cout<<"D "<<(d?"":"不")<<"是。"<<endl;     } return 0;}

（8）有等式[※×(※3+※)]2=8※※9，其中※處為1個數字，滴上了墨水無法辨認。請程式設計找出※表示哪個數字。

拓展：有等式[※×(※3○※)]2=8※※9，其中※處為1個數字，○處為+、-、×、÷四個運算子之一，現滴上了墨水無法辨認。請程式設計找出※表示哪個數字，○表示哪個運算子。

參考解答：用a,b,c,d,e分別代表※處的數字，有

#include<iostream>  using namespace std;  int main(){      int a,b,c,d,e,s;      for(a=0;a<=9;a++)      {          for(b=0;b<=9;b++)          {              for(c=0;c<=9;c++)              {                  for(d=0;d<=9;d++)                  {                      for(e=0;e<=9;e++)                      {                          s=a*(b*10+3+c);                          if (s*s==8000+d*100+e*10+9)                          {                              cout<<"等式為：["<<a<<"×("<<b<<"3+"<<c<<")]^2=8"<<d<<e<<"9)"<<endl;                          }                            }                  }              }          }      }  return 0;}   

執行結果

拓展：有等式[※×(※3○※)]^2=8※※9，其中※處為1個數字，○處為+、-、×、÷四個運算子之一，現滴上了墨水無法辨認。請程式設計找出※表示哪個數字，○表示哪個運算子。

參考解答：

#include<iostream>  using namespace std;  int main(){      int i,a,b,c,d,e,s;      for(a=0;a<=9;a++)      {          for(b=0;b<=9;b++)          {              for(c=0;c<=9;c++)              {                  for(d=0;d<=9;d++)                  {                      for(e=0;e<=9;e++)                      {                          s=a*(b*10+3+c);                          if (s*s==8000+d*100+e*10+9)                          {                              cout<<"等式為：["<<a<<"×("<<b<<"3+"<<c<<")]^2=8"<<d<<e<<"9)"<<endl;                          }       s=a*(b*10+3-c);                          if (s*s==8000+d*100+e*10+9)                          {                              cout<<"等式為：["<<a<<"×("<<b<<"3-"<<c<<")]^2=8"<<d<<e<<"9)"<<endl;                          }       s=a*((b*10+3)*c);                          if (s*s==8000+d*100+e*10+9)                          {                              cout<<"等式為：["<<a<<"×("<<b<<"3*"<<c<<")]^2=8"<<d<<e<<"9)"<<endl;                          }       if(c!=0)      {       s=a*((b*10+3)/c);         if (s*s==8000+d*100+e*10+9)         {          cout<<"等式為：["<<a<<"×("<<b<<"3÷"<<c<<")]^2=8"<<d<<e<<"9)"<<endl;         }      }                    }                  }              }          }      }     return 0; }  

執行結果

           

給我老師的人工智慧教程打call！http://blog.csdn.net/jiangjunshow