如何快速求出（在log2n的時間複雜度內）整數區間[x,y]中第k大的值（x<=k<=y）?

  其實我剛開始想的是用快排來查詢，但是其實這樣是不行的，因為會破壞原序列，就算另外一個數組來儲存，多次詢問的條件下，同樣滿足不了。

  劃分樹主要是針對上述問題而設計的。 劃分樹是一種基於線段樹的資料結構，其基本思想就是將待查詢的區間分為兩個子區間：不大於數列中間 值的元素被分配到左兒子的子區間，簡稱左子區間；大於數列中間值的元素被分配到右兒子的子區間，簡稱右子區間。

  顯然，左子區間的數小於右子區間的數。建樹 的時候要注意，對於被分到同一子樹的元素，元素間的相對位置不能改變。例如構建整數序列[1 5 2 3 6 4 7 3 0 0]的劃分樹：

  整數序列經排序後得到[0 0 1 2 3 3 4 5 6 7]，中間值是3。劃分出下一層的左子區間[1 2 3 0 0]，中間值為1；下一層的由子區間[5 6 4 7 3]，中間值為5；以中間值為界，劃分出當前層每個區間的下層左右子區間······以此類推，直至劃分出所有子區間含單個整數為止。

  這裡可能有人就會提問了，為什麼兩個子區間是這樣的呢？？  其實我剛開始也這麼想，下面給出解釋：

1.如果有和中間值相等的元素，插入進去的前提是  小於中間值的元素不夠填滿一個區間，差多少就補多少和中間值相等的元素（很好理解，小於肯定優先嘛）。

2.相對位置不能改變。

下面給出一個圖，還是以[1 5 2 3 6 4 7 3 0 0]為例：

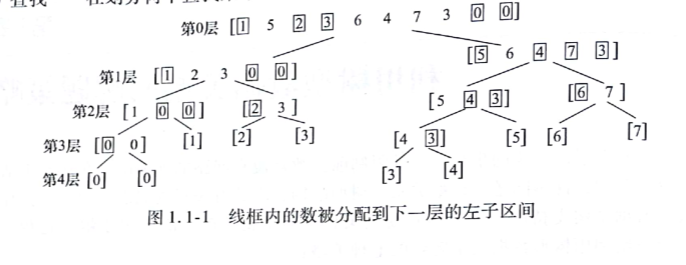
如圖可見，劃分樹是一顆完全二叉樹，樹葉為單元素區間。若數列含有n個整數，則對應的劃分樹有[log 2 n]+1層。

查詢的時候通過記錄進入左子樹的數的個數，確定下一個查詢區間，直至查詢範圍縮小到單元素為止。  此時，區間內的第K大值就找到了。

  整個演算法分兩步：

1.建樹-------離線構建整個查詢區間的劃分樹

2.查詢-------在劃分樹中查詢某個子區間中的第K大值。

  在查詢之前，我們先離線構建整個查詢區間的劃分樹。  建樹過程比較簡單，對於區間[l,r],首先通過對原數列排序找到這個區間的中間值的位置mid(mid=[(l+r)/2]),不大於中間值的數劃入左子樹[l,mid], 大於中間值的數劃入右子樹[mid+1,r] 。同時，對於第i 個數，記錄在[l,i] 區間內有多少整數被劃入左子樹。  最後繼續對它的左子樹[l,mid]  和右子樹[mid+1,r]  遞迴建樹，直至劃分出最後一層的葉節點為止，顯然，建樹過程是自上而下的。

  具體實現辦法：

  先將讀入的資料排序成sorted[]   (從小到大排序) ,取區間[l,r]的中間值sorted[mid]，然後遍歷[l,r]區間，依次將每個整數劃分到左子區間或者右子區間中去。  注意，被分到每個子樹的整數是相對有序的。  注意，這裡要記錄區間能插入多少個和中間值相等的元素。    另外，在這個過程中，要記錄一個類似字首和的東西，即  l  到  i  這個區間內有多少整數被劃分到左子樹。設：

tree [p][i] ------第p層第i個位置的整數值，初始序列為tree[0][]。

sorted[]---------排序序列，即儲存tree[0][]排序後的結果

toleftp[][]--------toleft[p][i],表示第p層前i