AES簡介及原始碼實現(C)
AES簡介及原始碼實現©
本blog的目的僅僅是記錄一個AES原理及其C程式碼實現,轉載自:https://blog.csdn.net/qq_28205153/article/details/55798628
感謝分享。
高階加密標準(AES,Advanced Encryption Standard)為最常見的對稱加密演算法(微信小程式加密傳輸就是用這個加密演算法的)。對稱加密演算法也就是加密和解密用相同的金鑰,具體的加密流程如下圖:
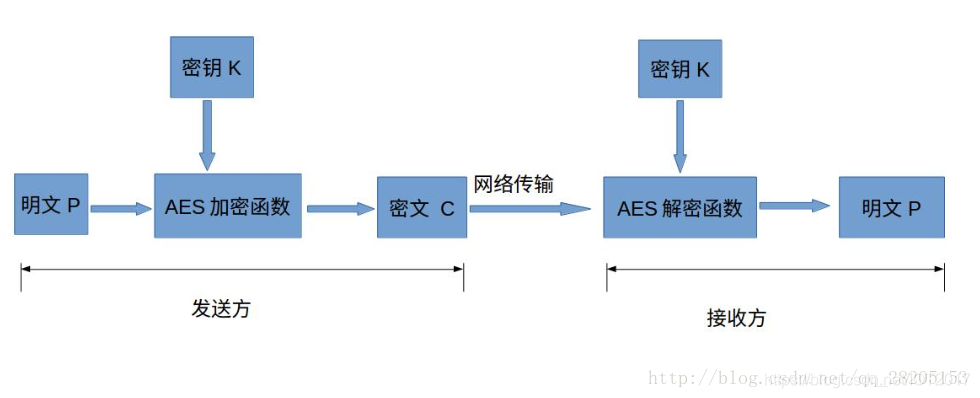
下面簡單介紹各部分的作用與意義:
- 明文P
沒有經過加密的資料。
- 金鑰K
用來加密明文的密碼,在對稱加密演算法中,加密與解密的金鑰是相同的。金鑰為接收方與傳送方協商產生,但不可以直接在網路上傳輸,否則會導致金鑰洩漏,通常是通過非對稱加密演算法加密金鑰,然後再通過網路傳輸給對方,或者直接面對面商量金鑰。金鑰是絕對不可以洩漏的,否則會被攻擊者還原密文,竊取機密資料。
- AES加密函式
設AES加密函式為E,則 C = E(K, P),其中P為明文,K為金鑰,C為密文。也就是說,把明文P和金鑰K作為加密函式的引數輸入,則加密函式E會輸出密文C。
- 密文C
經過加密處理後的資料。
- AES解密函式
設AES解密函式為D,則 P = D(K, C),其中C為密文,K為金鑰,P為明文。也就是說,把密文C和金鑰K作為解密函式的引數輸入,則解密函式會輸出明文P。
在這裡簡單介紹下對稱加密演算法與非對稱加密演算法的區別。
- 對稱加密演算法
加密和解密用到的金鑰是相同的,這種加密方式加密速度非常快,適合經常傳送資料的場合。缺點是金鑰的傳輸比較麻煩。
- 非對稱加密演算法
加密和解密用的金鑰是不同的,這種加密方式是用數學上的難解問題構造的,通常加密解密的速度比較慢,適合偶爾傳送資料的場合。優點是金鑰傳輸方便。常見的非對稱加密演算法為RSA、ECC和EIGamal。
實際中,一般是通過RSA加密AES的祕鑰,傳輸到接收方,接收方解密得到AES金鑰,然後傳送方和接收方用AES金鑰來通訊。
本文下面AES原理的介紹參考自《現代密碼學教程》,AES的實現在介紹完原理後開始。
AES的基本結構
AES為分組密碼,分組密碼也就是把明文分成一組一組的,每組長度相等,每次加密一組資料,直到加密完整個明文。AES標準規範中,分組長度只能是128位,也就是說,每個分組為16個位元組。金鑰長度可以使用128位、192位或256位、金鑰的長度不同,推薦的加密輪數也不同,如下表所示:
| AES | 金鑰長度(bit) | 分組長度(bit) | 加密輪數 |
|---|---|---|---|
| AES-128 | 128 | 128 | 10 |
| AES-192 | 192 | 128 | 12 |
| AES-256 | 256 | 128 | 14 |
輪數在下面介紹,這裡實現的是AES-128,也就是金鑰長度為128位,加密輪數為10輪。
上面說到AES的加密公式為C=E(K,P),在加密函式E中,會執行一個輪函式,並且執行10次這個輪函式,這個輪函式的前9次執行的操作是一樣的,只有第10次不同。也就是說,一個明文分組會被加密10輪。AES的核心就是實現一輪中的所有操作。
AES的處理單位是位元組,128位的輸入明文分組P和輸入祕鑰K都被分為16byte,分別記為P=P0 P1 … P15 和K=K0 K1…K15。如:明文分組為P=abcdefghijklmnop,其中的字元a對應P0,p對應P15。一般地,明文分組用位元組為單位的正方形矩陣描述,稱為狀態矩陣。在演算法的每一輪中,狀態矩陣的內容不斷髮生變化,最後的結果作為密文輸出。該矩陣中位元組的排列順序為從上到下、從左至右依次排列,如下圖所示
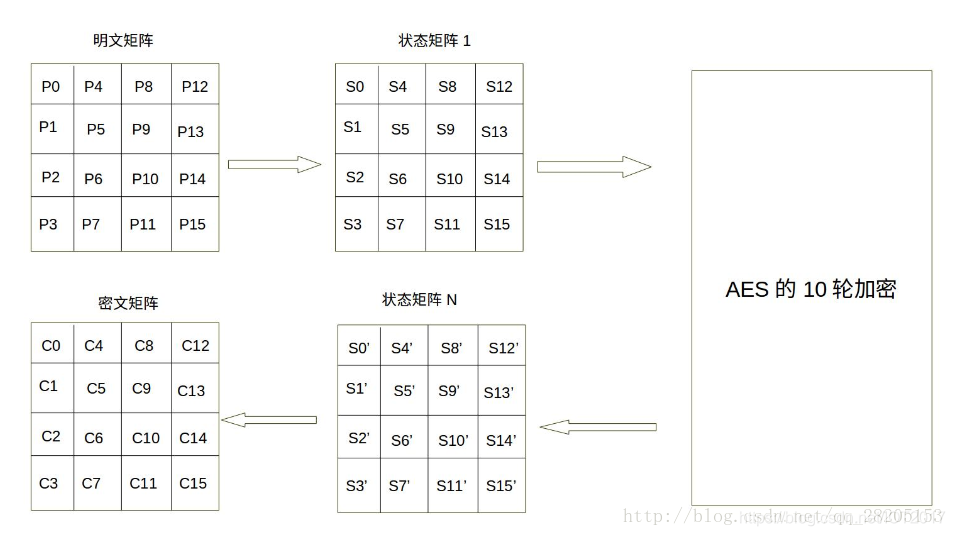
現在假設明文分組P為“abcdefghijklmnop”,則對應上面生成的狀態矩陣圖如下:
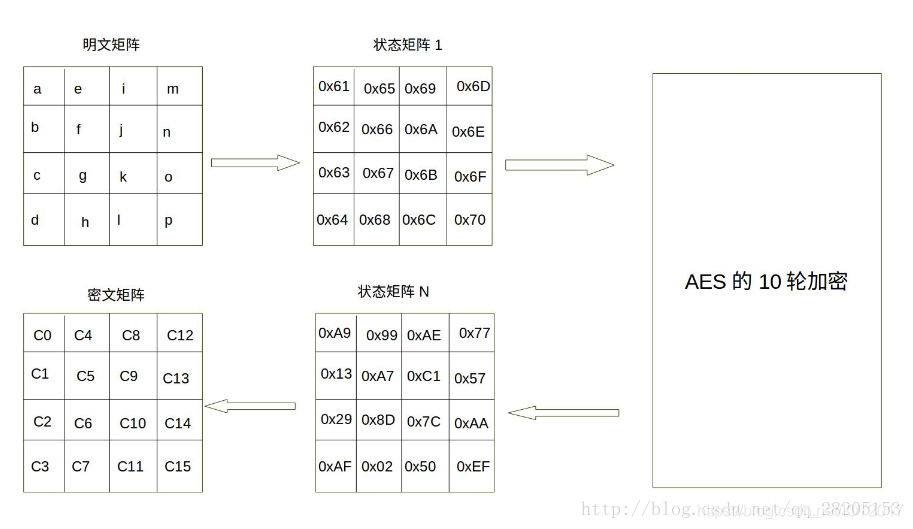
上圖中,0x61為字元a的十六進位制表示。可以看到,明文經過AES加密後,已經面目全非。
類似地,128位金鑰也是用位元組為單位的矩陣表示,矩陣的每一列被稱為1個32位bit字。通過金鑰編排函式,該金鑰矩陣被擴充套件成一個44個字組成的序列W[0],W[1],…,W[43],該序列的前4個元素W[0],W[1],W[2],W[3]是原始金鑰,用於加密運算中的初始金鑰加;後面40個字分為10組,每個組4個字(128bit),分別用於10輪加密運算中的輪金鑰加,如下圖所示:
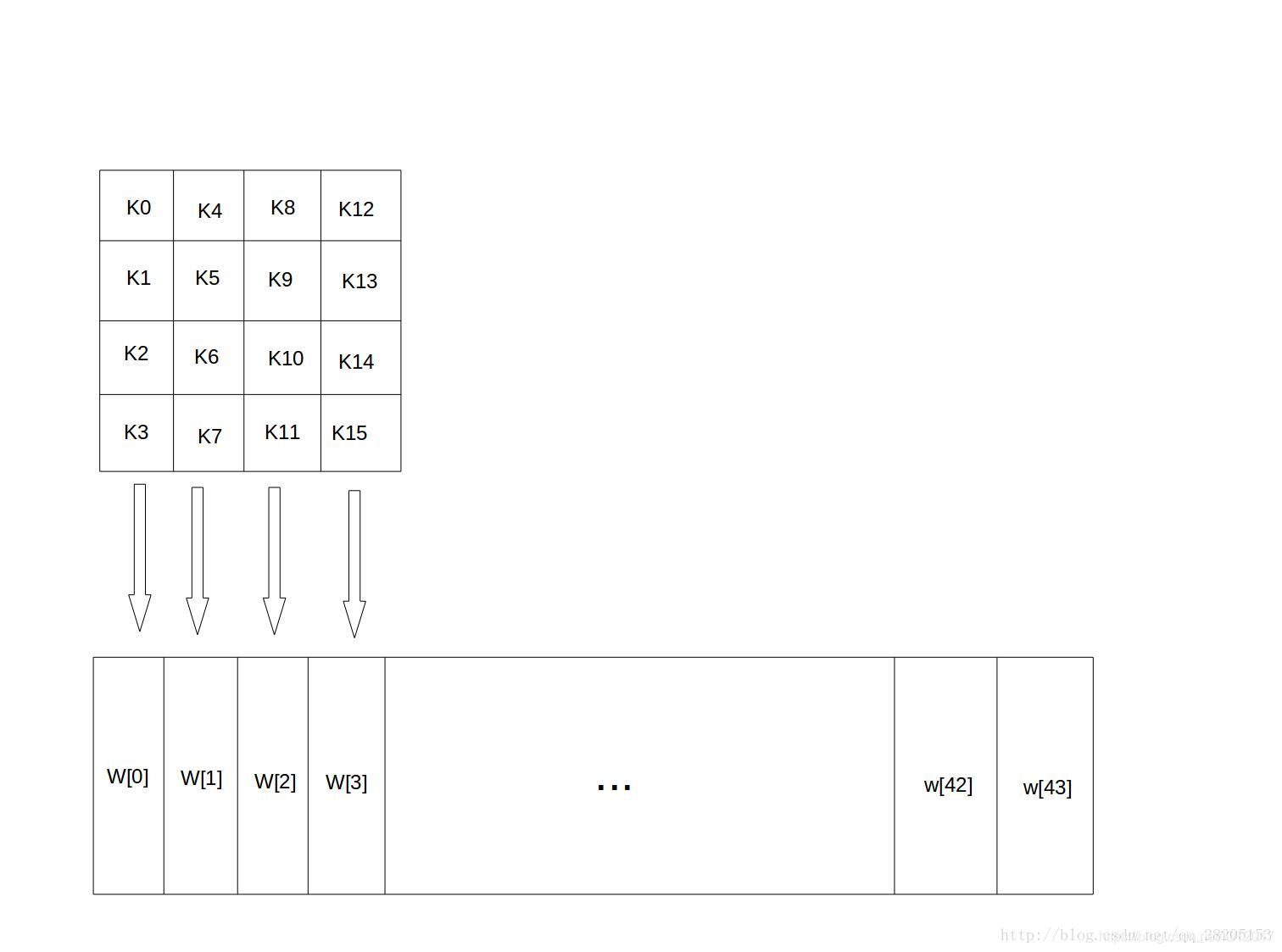
上圖中,設K=“abcdefghijklmnop”,則K0=a,K15=p,W[0]=K0 K1 K2 K3 = “abcd”。
AES的整體結構如下圖所示,其中的W[0,3]是指W[0]、W[1]、W[2]和W[3]串聯組成的128位金鑰。加密的第1輪到第9輪的輪函式是一樣的,包括4個操作:位元組代換、行位移、列混合和輪金鑰加。最後一輪迭代不執行列混合。另外,在第一輪迭代之前,先將明文和原始金鑰進行一次異或加密操作。
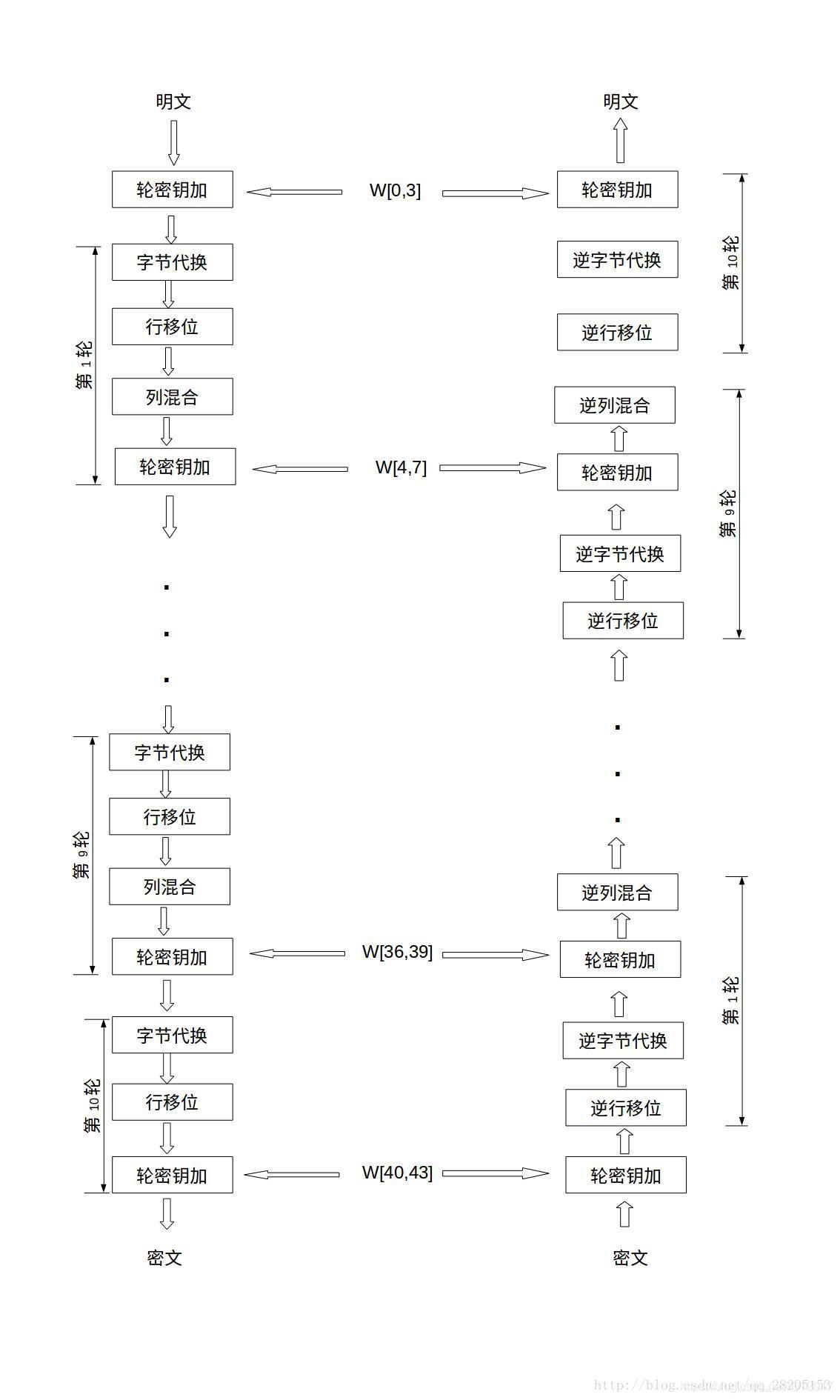
上圖也展示了AES解密過程,解密過程仍為10輪,每一輪的操作是加密操作的逆操作。由於AES的4輪(每一輪中的)操作都是可逆的,因此,解密操作的一輪就是順序執行逆行移位、逆位元組代換、輪金鑰加和逆列混合。同加密操作類似,最後一輪不執行逆列混合,在第1輪解密之前,要執行1次金鑰加操作。
下面分別介紹AES中的一輪的4個操作階段,這4個分操作階段使輸入位得到充分的混淆。
一、位元組代換
1位元組代換操作
AES的位元組代換其實就是一個簡單的查表操作。AES定義了一個S盒和一個逆S盒。
AES的S盒:
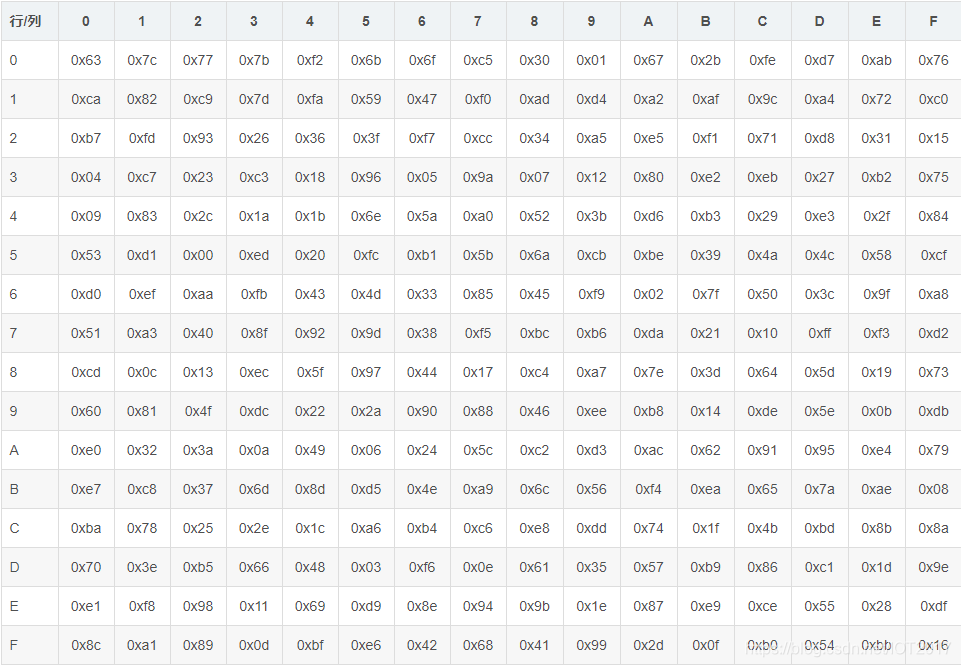
狀態矩陣中的元素按照下面的方式對映為一個新的位元組:把該位元組的高4位作為行值,低4位作為列值取出S盒或者逆S盒中對應的行的元素作為輸出。例如,加密時,輸出位元組S1為0x12,則查S盒的第0x01行和第0x02列,得到值0xc9,然後替換S1原有的0x12為0xc9。狀態矩陣經位元組代換後的圖如下:
(第二個字元0xAB查表後應該轉換為0x62的,感謝細心的朋友指出,有空再畫圖更正了)
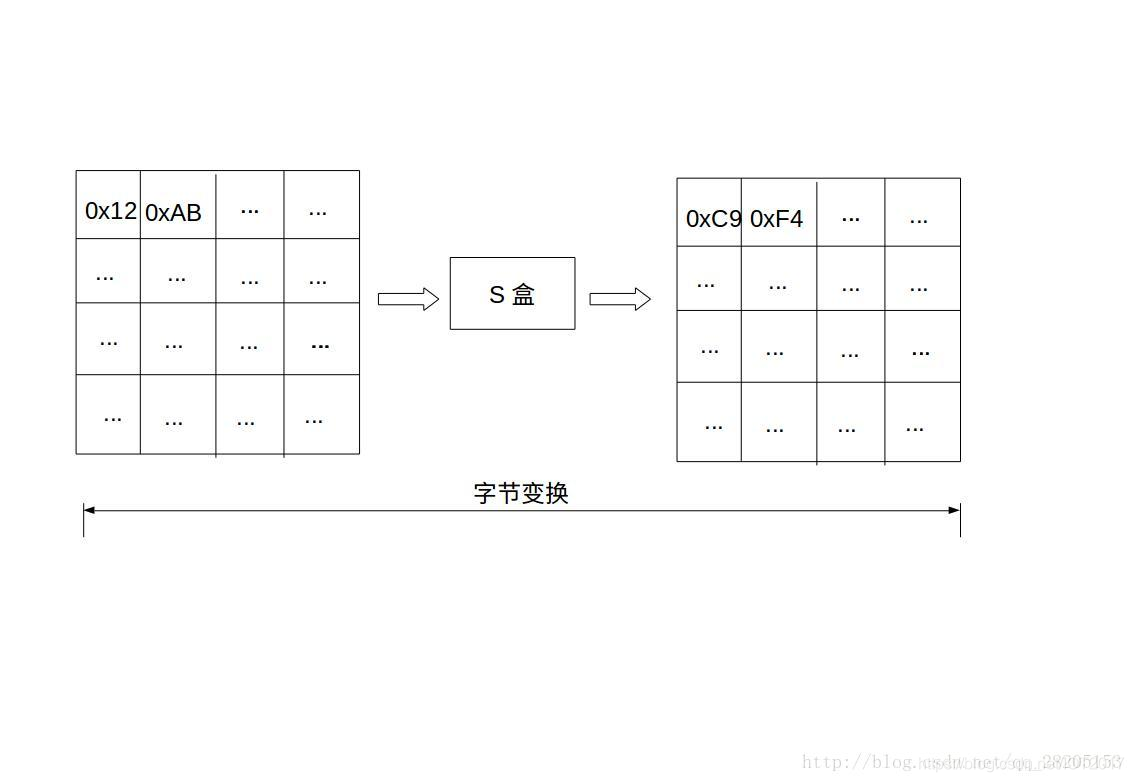
2.位元組代換逆操作
逆位元組滴啊換也就是查逆S盒來變換,逆S盒如下:

二、行位移
1.行位移操作
行位移是一個簡單的左迴圈移位操作。當金鑰長度位128bit時,狀態矩陣的第0行左移0位元組,第一行左移1位元組,第2行左移2位元組,第2行左移3位元組,如下圖所示:
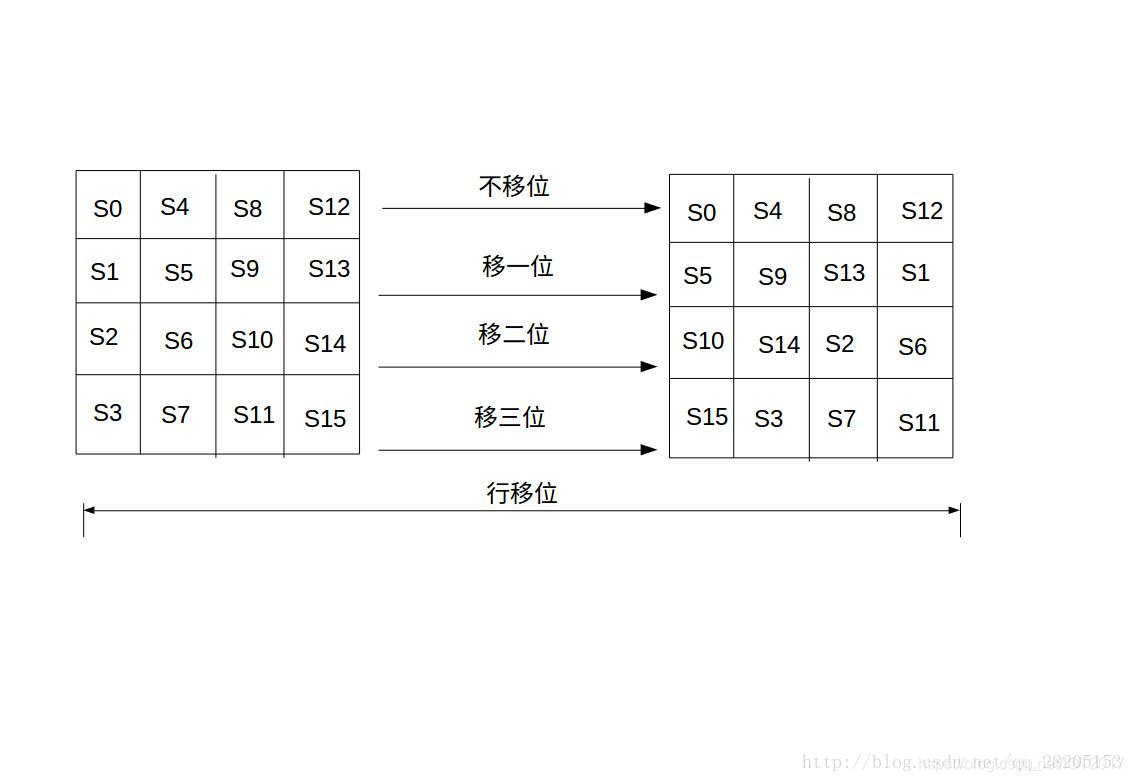
2.行位移的逆變換
行位移的逆變換是將狀態矩陣中的每一行執行相反的移位操作,例如AES-128中,狀態矩陣的第0行右移0位元組,第1行右移1位元組,第2行右移2位元組,第3行右移3位元組。
三、列混合
1.列混合操作
列混合變換是通過矩陣相乘來實現的,經行移位後的狀態矩陣與固定的矩陣相乘,得到混淆後的狀態矩陣,如下圖的公式所示:

狀態矩陣中的第j列(0 ≤j≤3)的列混合可以表示為下圖所示:
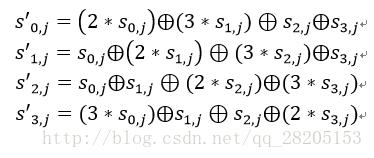
其中,矩陣元素的乘法和加法都是定義在基於GF(2^8)上的二元運算,並不是通常意義上的乘法和加法。這裡涉及到的一些資訊保安上的數學知識,不過不同這些知識也行。其實這種二元運算的加法等價於兩個位元組的異或,乘法則複雜一點。對於一個8位的二進位制數來說,使用域上的乘法乘以(00000010)等價於左移1位(低位補0)後,再根據情況同(00011011)進行異或運算,設S1=(a7 a6 a5 a4 a3 a2 a1 a0),則0x02 * S1如下圖所示:
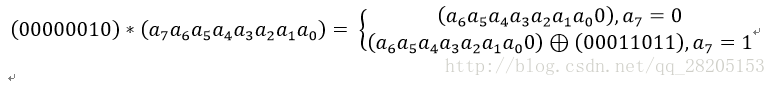
也就是說,如果a7為1,則進行異或運算,否則不進行。
類似地,乘以(00000100)可以拆分成兩次乘以(00000010)的運算:
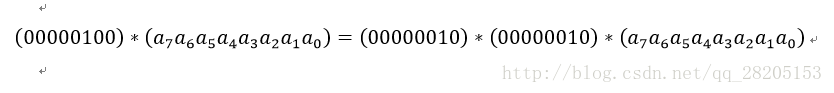
乘以(00000011)可已拆分成先分別乘以(00000001)和(00000010),再將兩個乘積異或:
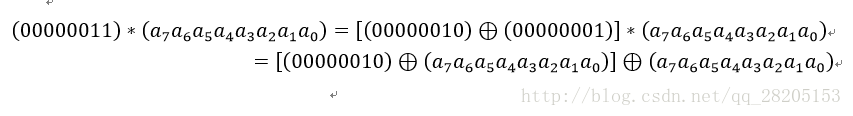
因此,我們只需要實現乘以2的函式,其他數字的乘法都可以通過組合來實現。
下面舉個具體的例子,輸入的矩陣狀態如下:
| C9 | E5 | FD | 2B |
| 7A | F2 | 78 | 6E |
| 63 | 9C | 26 | 67 |
| B0 | A7 | 82 | E5 |
下面,進行列混合運算:
以第一列的運算為例:

其他列的計算就不列舉了,列混合後生成的新狀態矩陣如下:
| D4 | E7 | CD | 66 |
| 28 | 02 | E5 | BB |
| BE | C6 | D6 | BF |
| 22 | 0F | DF | A5 |
2.列混合逆運算
逆向列混合變換可由下圖的矩陣乘法定義:

可以驗證,逆變換矩陣同正變換矩陣的乘積恰好為單位矩陣。
四、輪金鑰加
輪金鑰加是將128位輪金鑰Ki同狀態矩陣中的資料進行逐位異或操作,如下圖所示。其中,金鑰Ki中每個字W[4i],W[4i+1],W[4i+2],W[4i+3]為32位bit字,包含4個位元組,它們的生成演算法下面在下面介紹。輪金鑰加過程可以看成是字逐位異或的結果,也可以看成位元組級別或者位級別的操作。也就是說,可以看成S0 S1 S2 S3組成的32位字與W[4i]的異或運算。
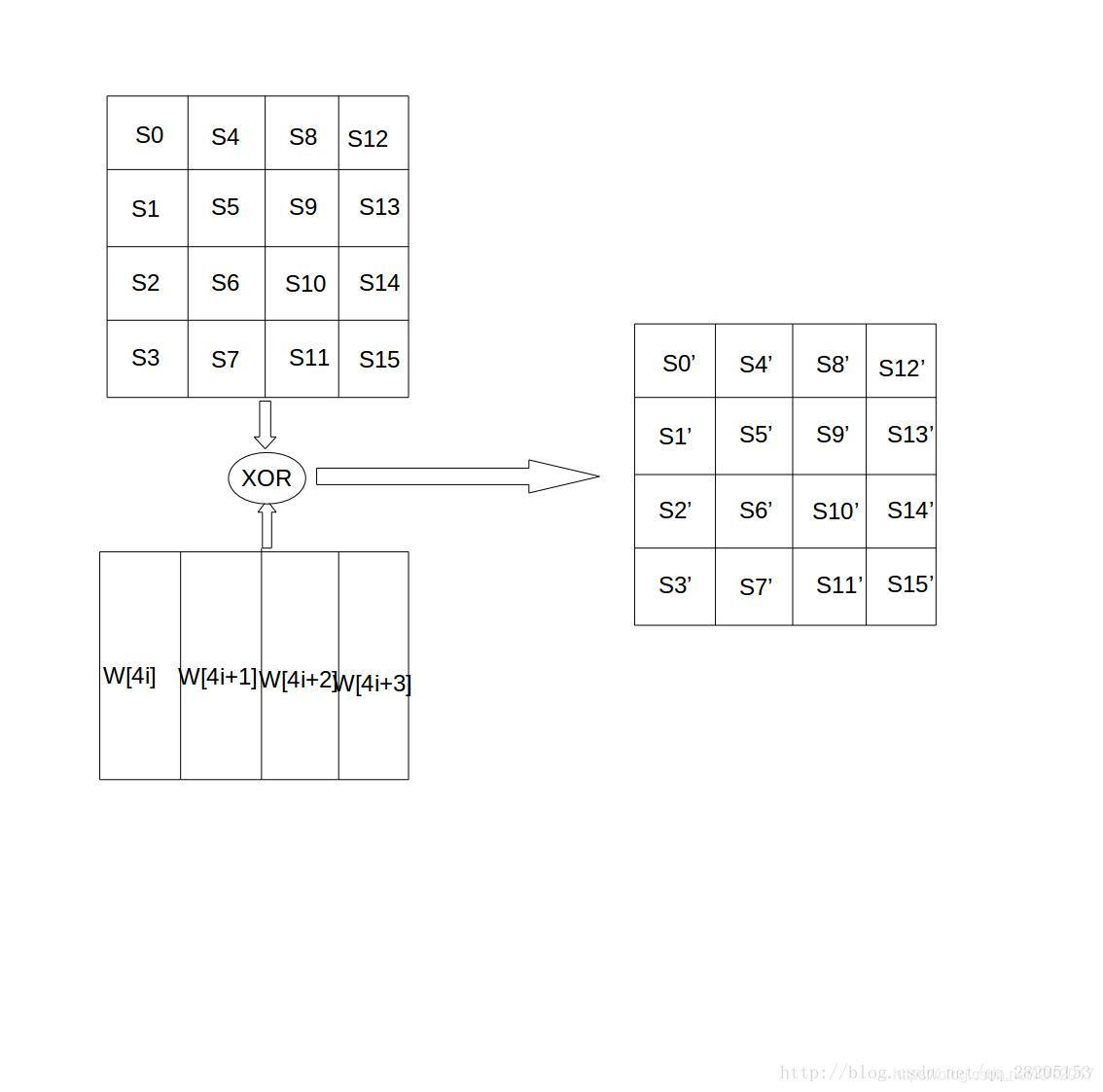
輪金鑰加的逆運算同正向的輪金鑰加運算完全一致,這是因為異或的逆操作是其自身。輪金鑰加非常簡單,但卻能夠影響S陣列中的每一位。
金鑰擴充套件
AES首先將初始金鑰輸入到一個44的狀態矩陣中,如下圖所示
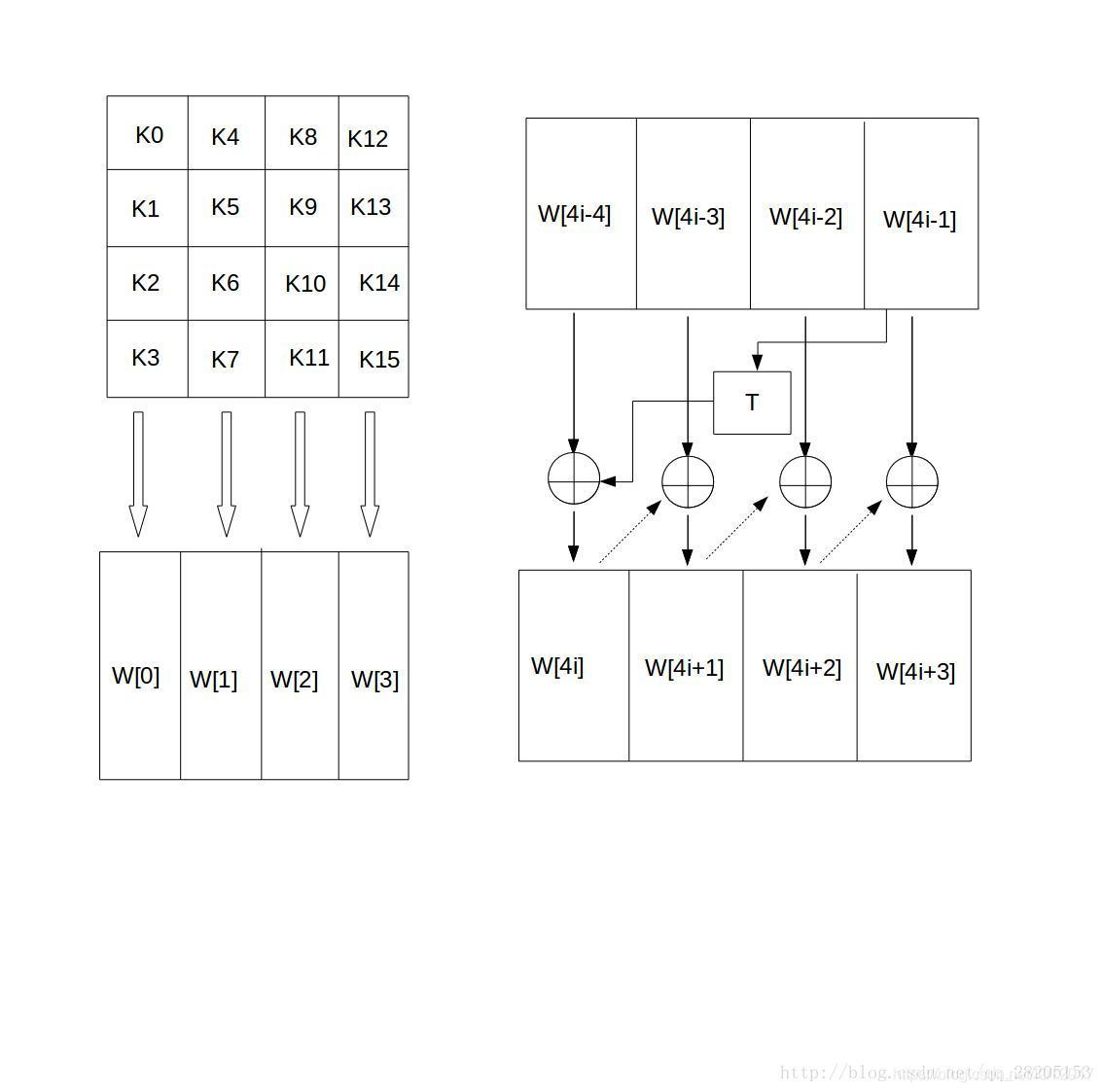
這個44矩陣的每一列的4個位元組組成一個字,矩陣4列的4個字一次命名為W[0]、W[1]、W[2]和W[3],它們構成一個以字為單位的陣列W。例如,設金鑰K為“abcdefghigklmnop”,則K0=‘a’,K1=‘b’,K2=‘c’,K3=‘d’,W[0]=“abcd”。
接著,對W陣列擴充40個新列,構成總共44列的擴充套件金鑰陣列。新列以如下的遞迴方式產生:
1.如果i不是4的倍數,那麼第i列由如下等式確定:
W[i]=W[i-4]⨁W[i-1]
2.如果i是4的倍數,那麼第i列由如下等式確定:
W[i]=W[i-4]⨁T(W[i-1])
其中,T是一個有點兒複雜的函式。
函式T由3部分組成:字迴圈、位元組代換和輪常量異或,這3部分的作用分別如下。
a.字迴圈:將1個字中的4個位元組迴圈左移1個位元組。即將輸入字[b0 b1 b2 b3]變換成[b1 b2 b3 b0]。
b. 位元組代換:對字迴圈的結果使用S盒進行位元組代換。
c.輪常量異或:將前兩步的結果同輪常量Rcon[j]進行異或,其中j表示輪數。
輪常量Rcon[j]是一個字,其值見下表。
| j | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Rcon[j] | 01 00 00 00 | 02 00 00 00 | 04 00 00 00 | 08 00 00 00 | 10 00 00 00 |
| j | 6 | 7 | 8 | 9 | 10 |
| Rcon[j] | 20 00 00 00 | 40 00 00 00 | 80 00 00 00 | 1B 00 00 00 | 36 00 00 00 |
下面舉個例子:
設初始的128位金鑰為:
3C 1A 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD
那麼4個初始值為:
W[0]= 3C 1A 0B 21
W[1]= 57 F0 19 16
W[2]= 90 2E 13 80
W[3]= AC C1 07 BD
下面求擴充套件的第1輪的子金鑰(W[4],W[5],W[6],W[7])。
由於4是4的倍數,所以:
W[4] = W[0] ⨁ T(W[3])
T(W[3])的計算步驟如下:
- 迴圈地將W[3]的元素移位:AC C1 07 BD變成C1 07 BD AC;
- 將 C1 07 BD AC 作為S盒的輸入,輸出為78 C5 7A 91;
- 將78 C5 7A 91與第一輪輪常量Rcon[1]進行異或運算,將得到79 C5 7A 91,因此,T(W[3])=79 C5 7A 91,故
W[4] = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0
其餘的3個子金鑰段的計算如下:
W[5] = W[1] ⨁ W[4] = 57 F0 19 16 ⨁ 45 64 71 B0 = 12 94 68 A6
W[6] = W[2] ⨁ W[5] =90 2E 13 80 ⨁ 12 94 68 A6 = 82 BA 7B 26
W[7] = W[3] ⨁ W[6] = AC C1 07 BD ⨁ 82 BA 7B 26 = 2E 7B 7C 9B
所以,第一輪的金鑰為 45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B。
AES解密
在文章開始的圖中,有AES解密的流程圖,可以對應那個流程圖來進行解密。下面介紹的是另一種等價的解密模式,流程圖如下圖所示。這種等價的解密模式使得解密過程各個變換的使用順序同加密過程的順序一致,只是用逆變換取代原來的變換。
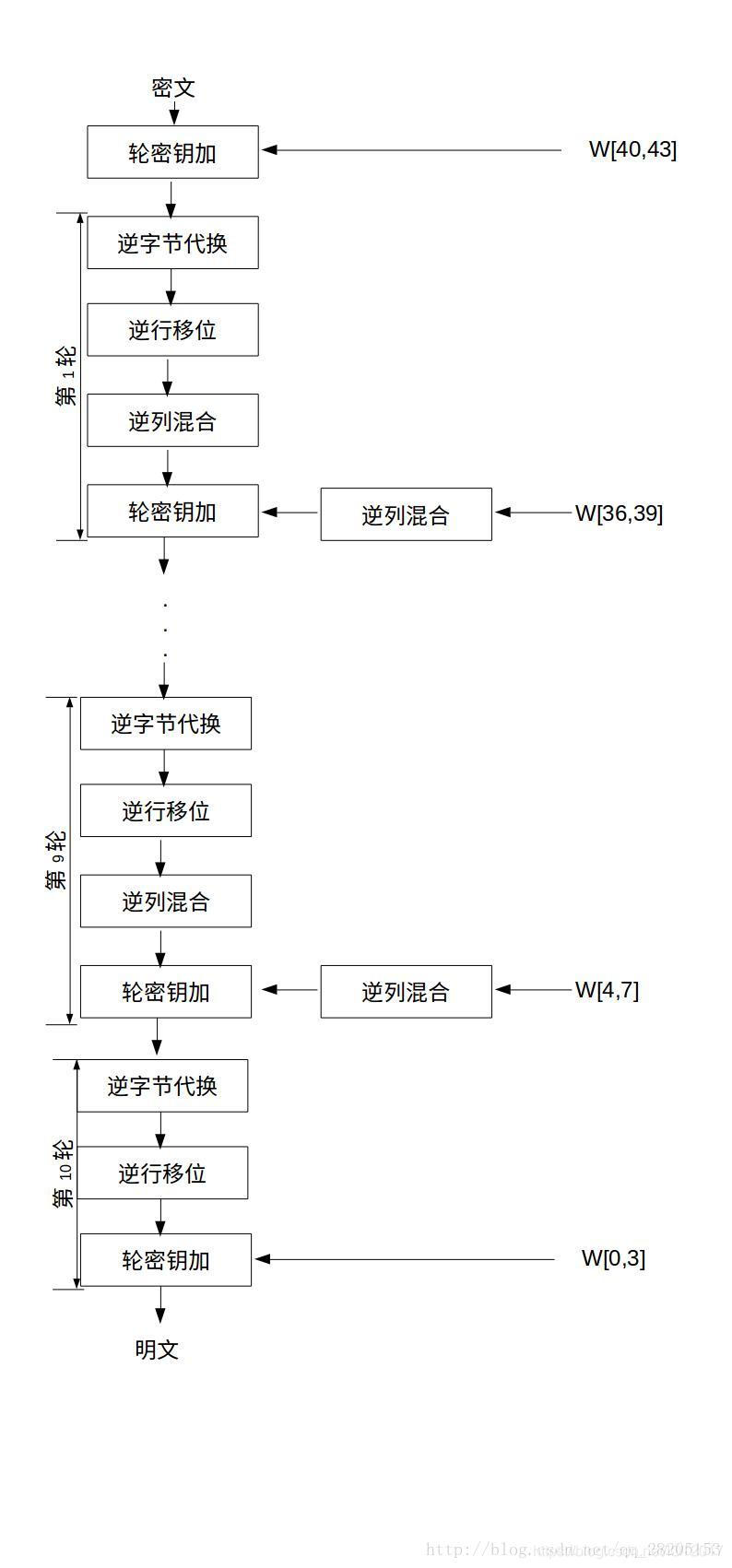
AES原理到這裡就結束了,下面主要為AES的實現,對以上原理中的每一個小節進行實現講解,講解的時候會插入一些關鍵程式碼,完整的程式碼參見文章最後。文章最後提供兩個完整的程式,一個能在linux下面編譯執行,一個能在VC6.0下面編譯通過。
AES演算法實現
AES加密函式預覽
aes加密函式中,首先進行金鑰擴充套件,然後把128bit位長度的字串讀進一個4*4整數陣列中,這個陣列就是狀態矩陣。例如,pArray[0][0]=S0,pArray[1][0]=S1,pArray[0][1]=S4。這個讀取過程是通過 convertToIntArray()函式來實現的。每個輪操作的函式都對pArray進行修改,也就是對狀態矩陣進行混淆。在執行完10輪加密後,會把pArray轉換回字串,再存入明文p的字元陣列中,所以,在加密完後,明文p的字串中的字元就是加密後的字元了。這個轉換過程是通過convertArrayToStr()函式來實現的。
/**
* 引數 p: 明文的字串陣列。
* 引數 plen: 明文的長度。
* 引數 key: 金鑰的字串陣列。
*/
void aes(char *p, int plen, char *key){
int keylen = strlen(key);
if(plen == 0 || plen % 16 != 0) {
printf("明文字元長度必須為16的倍數!\n");
exit(0);
}
if(!checkKeyLen(keylen)) {
printf("金鑰字元長度錯誤!長度必須為16、24和32。當前長度為%d\n",keylen);
exit(0);
}
extendKey(key);//擴充套件金鑰
int pArray[4][4];
for(int k = 0; k < plen; k += 16) {
convertToIntArray(p + k, pArray);
addRoundKey(pArray, 0);//一開始的輪金鑰加
for(int i = 1; i < 10; i++){//前9輪
subBytes(pArray);//位元組代換
shiftRows(pArray);//行移位
mixColumns(pArray);//列混合
addRoundKey(pArray, i);
}
//第10輪
subBytes(pArray);//位元組代換
shiftRows(pArray);//行移位
addRoundKey(pArray, 10);
convertArrayToStr(pArray, p + k);
}
}
1.金鑰擴充套件的實現
在開始加密前,必須先獲得第一輪加密用到的金鑰,故先實現金鑰擴充套件 。
下面是金鑰擴充套件函式的實現,這個函式傳入金鑰key的字串表示,然後從字串中讀取W[0]到W[3],函式getWordFromStr()用於實現此功能。讀取後,就開始擴充套件金鑰,當i是4的倍數的時候,就會呼叫T()函式來進行擴充套件,因為T函式的行為與加密的輪數有關,故要把加密的輪數 j 作為引數傳進去。
//金鑰對應的擴充套件陣列
static int w[44];
/**
* 擴充套件金鑰,結果是把w[44]中的每個元素初始化
*/
static void extendKey(char *key) {
for(int i = 0; i < 4; i++)
w[i] = getWordFromStr(key + i * 4);
for(int i = 4, j = 0; i < 44; i++) {
if( i % 4 == 0) {
w[i] = w[i - 4] ^ T(w[i - 1], j);
j++;//下一輪
}else {
w[i] = w[i - 4] ^ w[i - 1];
}
}
}
下面是T()函式的程式碼實現,T()函式中接收兩個引數,引數num為上面傳進的W[i - 1],round為加密的輪數。首先用一個numArray儲存從32位的W[i-1]中取得4個位元組。如果W[i-1]為0x12ABCDEF,那麼numArray[0] = 0x12,numArray[1] = 0xAB。函式splitIntToArray()用於從32位整數中讀取這四個位元組,之所以這樣做是因為整數陣列比較容易操作。然後呼叫leftLoop4int()函式把numArray陣列中的4個元素迴圈左移1位。然後執行位元組代換,通過getNumFromSBox()函式來獲取S盒中相應的值來替換numArray中的值。接著通過mergeArrayToInt()函式把位元組代換後的numArray合併回32位的整數,在進行輪常量異或後返回。
/**
* 常量輪值表
*/
static const int Rcon[10] = { 0x01000000, 0x02000000,
0x04000000, 0x08000000,
0x10000000, 0x20000000,
0x40000000, 0x80000000,
0x1b000000, 0x36000000 };
/**
* 金鑰擴充套件中的T函式
*/
static int T(int num, int round) {
int numArray[4];
splitIntToArray(num, numArray);
leftLoop4int(numArray, 1);//字迴圈
//位元組代換
for(int i = 0; i < 4; i++)
numArray[i] = getNumFromSBox(numArray[i]);
int result = mergeArrayToInt(numArray);
return result ^ Rcon[round];
}
2.位元組代換的實現
位元組代換的程式碼很簡單,就是把狀態矩陣中的每個元素傳進getNumFromSBox()函式中,然後取得前面8位中的高4位作為行值,低4位作為列值,然後返回S[row][col],這裡的S是儲存S盒的陣列。
/**
* 根據索引,從S盒中獲得元素
*/
static int getNumFromSBox(int index) {
int row = getLeft4Bit(index);
int col = getRight4Bit(index);
return S[row][col];
}
/**
* 位元組代換
*/
static void subBytes(int array[4][4]){
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
array[i][j] = getNumFromSBox(array[i][j]);
}
3.行移位的實現
行移位的時候,首先把狀態矩陣中第2,3,4行復製出來,然後對它們行進左移相應的位數,然後再複製回去狀態矩陣array中。
/**
* 將陣列中的元素迴圈左移step位
*/
static void leftLoop4int(int array[4], int step) {
int temp[4];
for(int i = 0; i < 4; i++)
temp[i] = array[i];
int index = step % 4 == 0 ? 0 : step % 4;
for(int i = 0; i < 4; i++){
array[i] = temp[index];
index++;
index = index % 4;
}
}
/**
* 行移位
*/
static void shiftRows(int array[4][4]) {
int rowTwo[4], rowThree[4], rowFour[4];
//複製狀態矩陣的第2,3,4行
for(int i = 0; i < 4; i++) {
rowTwo[i] = array[1][i];
rowThree[i] = array[2][i];
rowFour[i] = array[3][i];
}
//迴圈左移相應的位數
leftLoop4int(rowTwo, 1);
leftLoop4int(rowThree, 2);
leftLoop4int(rowFour, 3);
//把左移後的行復制回狀態矩陣中
for(int i = 0; i < 4; i++) {
array[1][i] = rowTwo[i];
array[2][i] = rowThree[i];
array[3][i] = rowFour[i];
}
}
4.列混合的實現
列混合函式中,先把狀態矩陣初始狀態複製一份到tempArray中,然後把tempArray與colM矩陣相乘,colM為存放要乘的常數矩陣的陣列。其中的GFMul()函式定義了矩陣相乘時的乘法,加法則直接通過異或來實現。GFMul()通過呼叫乘以各個數對應的函式來實現乘法。例如,S1 * 2 剛通過呼叫GFMul2(S1)來實現。S1 * 3 剛通過GFMul3(S1)來實現。在這裡,主要實現GFMul2()函式就行了,其它的都可以通過GFMul2()的組合來實現。舉個例子吧,為計算下面這條等式,需要像下面這樣呼叫函式
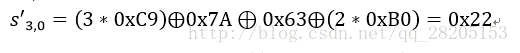
s = GFMul3(0xC9) ^ 0x7A ^ 0x63 ^ GFMul2(0xB0)
/**
* 列混合要用到的矩陣
*/
static const int colM[4][4] = { 2, 3, 1, 1,
1, 2, 3, 1,
1, 1, 2, 3,
3, 1, 1, 2 };
static int GFMul2(int s) {
int result = s << 1;
int a7 = result & 0x00000100;
if(a7 != 0) {
result = result & 0x000000ff;
result = result ^ 0x1b;
}
return result;
}
static int GFMul3(int s) {
return GFMul2(s) ^ s;
}
/**
* GF上的二元運算
*/
static int GFMul(int n, int s) {
int result;
if(n == 1)
result = s;
else if(n == 2)
result = GFMul2(s);
else if(n == 3)
result = GFMul3(s);
else if(n == 0x9)
result = GFMul9(s);
else if(n == 0xb)//11
result = GFMul11(s);
else if(n == 0xd)//13
result = GFMul13(s);
else if(n == 0xe)//14
result = GFMul14(s);
return result;
}
/**
* 列混合
*/
static void mixColumns(int array[4][4]) {
int tempArray[4][4];
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
tempArray[i][j] = array[i][j];
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++){
array[i][j] = GFMul(colM[i][0],tempArray[0][j]) ^ GFMul(colM[i][1],tempArray[1][j])
^ GFMul(colM[i][2],tempArray[2][j]) ^ GFMul(colM[i][3], tempArray[3][j]);
}
}
5.輪金鑰加的實現
輪金鑰加的實現很簡單,就是根據傳入的輪數來把狀態矩陣與相應的W[i]異或。
/**
* 輪金鑰加
*/
static void addRoundKey(int array[4][4], int round) {
int warray[4];
for(int i = 0; i < 4; i++) {
splitIntToArray(w[ round * 4 + i], warray);
for(int j = 0; j < 4; j++) {
array[j][i] = array[j][i] ^ warray[j];
}
}
}
6.AES解密函式
AES的解密函式和加密函式有點不同,可以參考上面的等價解密流程圖來理解,解密函式中呼叫的是各輪操作的逆函式。逆函式在這裡就不詳細講解了,可以參考最後的完整程式碼。
/**
* 引數 c: 密文的字串陣列。
* 引數 clen: 密文的長度。
* 引數 key: 金鑰的字串陣列。
*/
void deAes(char *c, int clen, char *key) {
int keylen
相關推薦
AES簡介及原始碼實現(C)
AES簡介及原始碼實現©
本blog的目的僅僅是記錄一個AES原理及其C程式碼實現,轉載自:https://blog.csdn.net/qq_28205153/article/details/55798628 感謝分享。
高階加密標準(AES,Advanced Encr
[資料結構]Trie簡介及Python實現
Trie簡介及Python實現
Trie簡介
Python實現
Trie簡介
Trie即字首樹或字典樹,利用字串公共字首降低搜尋時間。速度為
O
深入淺出學Vue開發:第四章、Vue的生命週期及原始碼實現
歡迎大家訪問我的個人網站 - Sunday俱樂部
通過上面兩章的學習,我們已經學會了Vue的所有基礎語法,包括:
1、{{Mustache}} 語法 2、v-if、v-else、v-else-if、v-show 3、v-for 4、v-bind 5、v-mo
25 驅動裝置申請及原始碼實現裝置檔案建立一體函式(miscdevice)
驅動裝置申請及原始碼實現裝置檔案建立一體函式(miscdevice)
miscdevice是字元裝置驅動的簡化版本,方便實現一個簡單的字元裝置驅動。 只適用於沒有同類型的裝置驅動,也就是一個驅動只對應一個硬體。
相關變數及函式:
#include <lin
AVL樹簡介及Java實現
AVL樹簡介
AVL樹是被最先發明的一種較為簡單的平衡二叉查詢樹。
它的特點是:
1.本身首先是一棵二叉查詢樹。
2.帶有平衡條件:每個結點的左右子樹的高度之差的絕對值(平衡因子LoadFactor)最多為1。(設根結點的高度為1)
上面的兩張圖片,左邊的是AV
Deeplearning4j原始碼研習(1): BP演算法原理及原始碼實現
對於神經網路來講,訓練的過程是在更新網路權重和偏重的值,採取的方法有梯度下降、牛頓法等。由於深度學習通常有較多的網路層數,引數較多,而且二階的優化演算法本身就非常消耗記憶體,因此,實際應用中,梯度下降運用較多。梯度下降更新模型引數的公式:
式子中的代表網路中的某一個需要訓練的權重引數,
粒子群優化演算法(PSO)簡介及MATLAB實現
目錄
粒子群優化演算法概述
• 粒子群優化(PSO, particle swarm optimization)演算法是計算智慧領域,除了蟻群演算法,魚群演算法之外的一種群體智慧的優化演算法,該演算法最早由Kennedy和Eberhart在1995年提出的,
stl--分析空間配置器及原始碼實現
最近真是懶癌犯了,好久沒動過部落格了。開學兩個月了,每天基本都“住”在網咖了,沒日沒夜和舍友打遊戲。可是畢竟大三狗,找實習的壓力真是大。是時候搞出點事情了。
前兩天把stl的空間配置器的思路搞懂了,今天就把一二級配置器自己實現了一番,簡直爽,原始碼果然博大精深,只可惜我道行
OssMetro網盤簡介及原始碼
一 簡介
OssMetro網盤是基於阿里雲OSS服務開發的一款介面美觀,功能強大的網盤應用。介面採用metro風格,使用在官網.Net SDK基礎上開發的OSS .NET 4.5 SDK。執行需要安裝.NET 4.5 Framework。
二 本客戶
LSTM模型簡介及Tensorflow實現
LSTM模型在RNN模型的基礎上新增加了單元狀態C(cell state)。
一. 模型的輸入和輸出
在t時刻,LSTM的輸入有3個:
(1) 當前時刻LSTM的輸入值x(t);
(2) 上一時刻LSTM的輸出值h(t-1);
(3) 上一時刻的單
spark shuffle 發展變遷及原始碼實現
本文主要分享關於spark shuffle優秀文章彙總,通過這幾篇文章,能由淺入深學習spark shuffle過程。
shuffle write和shuffle read的理論解讀:
spark shuffle 過程理論解讀
決策樹學習(上)——深度原理剖析及原始碼實現
引言
本文給大家分享的主題是決策樹(Decision Tree)的原理剖析並附上程式碼實現供大家參考。由於基於決策樹的演算法較多,因此文章分為上下篇。上篇主要剖析決策樹原理、需要掌握的資訊理論知識以及Java原始碼實現等內容。下篇內容包括基於決策樹的ID3、C
Spring原始碼分析之IOC的三種常見用法及原始碼實現(二)
Spring原始碼分析之IOC的三種常見用法及原始碼實現(二)
回顧上文 我們研究的是
AnnotationConfigApplicationContext annotationConfigApplication = new AnnotationConfigApplicationContext
vue系列---理解Vue中的computed,watch,methods的區別及原始碼實現(六)
閱讀目錄
一. 理解Vue中的computed用法
二:computed 和 methods的區別?
三:Vue中的watch的用法
四:computed的基本原理及原始碼實現
回到頂部
一. 理解Vue中的computed用法
computed是計算屬性的; 它會根據所依賴
資料結構圖文解析之:樹的簡介及二叉排序樹C++模板實現.
閱讀目錄
0. 資料結構圖文解析系列
1. 樹的簡介
1.1 樹的特徵
1.2 樹的相關概念
2. 二叉樹簡介
2.1 二叉樹的定義
2.2 斜樹、滿二叉樹、完全二叉樹、二叉查詢樹
2
C# winform框架 音樂播放器開發 聯網下載音樂功能的實現原理及原始碼(純原創--)
首先 ,我做下載音樂功能;主要是為了探究它是怎麼實現的;所以介面很醜,不要在意哈----
接下來進入正題:
1.首先: 介面中下載音樂的部分主要是由3個segment組成::
一個textbox,用於輸入比如你喜歡的歌曲名/歌手;;
第二個是button1 這是主
資料結構圖文解析之:棧的簡介及C++模板實現
0. 資料結構圖文解析系列
1. 棧的簡介
1.1棧的特點
棧(Stack)是一種線性儲存結構,它具有如下特點:
棧中的資料元素遵守”先進後出"(First In Last Out)的原則,簡稱FILO結構。
限定只能在棧頂進行插入和刪除操作。
1.2棧的相關概念
棧的相關概念:
棧頂與棧底:允許元素
UDP flood 原理及原始碼 C實現
UDP是一種不可靠的、無連線的資料報服務。源主機在傳送資料前不需要和目標主機建立連線。資料被冠以源、目標埠號等UDP報頭欄位後直接發往目的主機。這時,每個資料段的可靠性依靠上層協議來保證。在傳送資料較少、較小的情況下,UDP比TCP更加高效。
如圖示,UDP報文結
C++ 泛型程序設計與STL模板庫(1)---泛型程序設計簡介及STL簡介與結構
urn 向上 隊列 是把 鏈表 需要 input stack 特定 泛型程序設計的基本概念
編寫不依賴於具體數據類型的程序
將算法從特定的數據結構中抽象出來,成為通用的
C++的模板為泛型程序設計奠定了關鍵的基礎
術語:概念
用來界定具備一定功能的數據類型。例如:
C#可擴展編程之MEF學習筆記(一):MEF簡介及簡單的Demo(轉)
com ring this exec hosting code .cn 引用 展開 在文章開始之前,首先簡單介紹一下什麽是MEF,MEF,全稱Managed Extensibility Framework(托管可擴展框架)。單從名字我們不難發現:MEF是專門致力於解決擴展性
