二叉樹的後序遍歷-遞迴和非遞迴演算法
阿新 • • 發佈:2018-11-17
同樣的,建立的演算法在先序中有,略去。
- 後序遞迴遍歷演算法
void PostOrder(BiTree bt){
if(bt){
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout<<bt->data<<" ";
}
}
- 後序非遞迴演算法
思想:
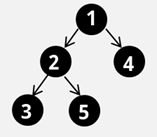
先序序列: 1 、2 、3 、5 、4
後序序列: 3 、5、2 、4 、1
把後續序列逆序得:
逆序後的後序序列:1 、4 、2 、5 、3
觀察,逆序後序列和先序序列有一定聯絡,逆序後的序列可以看做:是先序序列中對其左右子樹遍歷順序交換得到的結果。
- 根據根劃分出左右的子樹(先序序列)
1 、 [2 、3 、5] 、 [4]
- 交換根的左右子樹遍歷序列
1 、 [4] 、 [2 、 3 、 5]
- 交換以2為根的左右子樹遍歷序列
1 、 [4] 、 [2 、 5 、 3]
- 整體逆序得到後序序列:
3 、 5 、 2 、 4 、 1
程式碼:
void PostOrder(BiTree bt){ BiTree stack[20]; BiTree result[20]; int top1 = -1, top2=-1; stack[++top1] = bt; while(top1!=-1){ bt = stack[top1--]; result[++top2] = bt; //只用來反向最後的一趟的結果 /* 由於棧的特點就是後進先出,所以左子樹先入棧,然後出去的時候 是右子樹先出棧,故而這裡就完成了第一次的左右子樹的交換 */ if(bt->lchild!=NULL){ stack[++top1] = bt->lchild; } if(bt->rchild!=NULL){ stack[++top1] = bt->rchild; } } while(top2!=-1){ bt = result[top2--]; cout<<bt->data<<" "; } }
作者:無涯明月
發文時間:2018-11-16
