二叉樹——前序遍歷、中序遍歷、後序遍歷、層序遍歷詳解(遞迴非遞迴)
前言
- 前面介紹了二叉排序樹的構造和基本方法的實現。但是排序遍歷也是比較重要的一環。所以筆者將
前中後序.和層序遍歷梳理一遍。 - 瞭解樹的遍歷,需要具有的只是儲備有
佇列,遞迴,和棧。這裡筆者都有進行過詳細介紹,可以關注筆者資料結構與演算法專欄。持續分享,共同學習。
層序遍歷
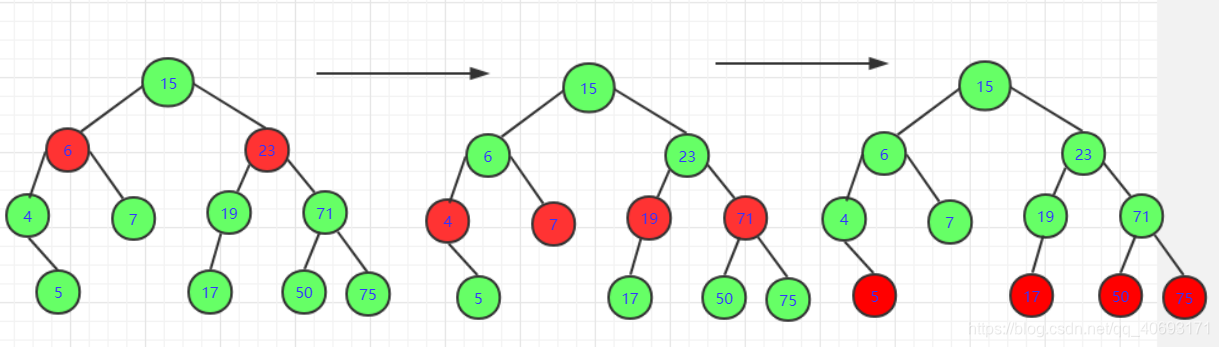
層序遍歷。聽名字也知道是按層遍歷。我們知道一個節點有左右節點。而每一層一層的遍歷都和左右節點有著很大的關係。也就是我們選用的資料結構不能一股腦的往一個方向鑽,而左右應該均衡考慮。這樣我們就選用佇列來實現。
- 對於佇列,現進先出。從根節點的節點push到佇列,那麼佇列中先出來的順序是第二層的左右(假設有)。
第二層每個執行的時候添加到佇列,那麼新增的所有節點都在第二層後面。 - 同理,假設開始
pop遍歷第n層的節點,每個節點會push左右兩個節點進去。但是佇列先進先出。它會放到隊尾(下一層)。直到第n層的最後一個pop出來,第n+1層的還在佇列中整齊排著。這就達到一個層序的效果。
實現的程式碼也很容易理解:
public void cengxu(node t) {//層序遍歷 Queue<node> q1 = new ArrayDeque<node>(); if (t == null) return; if (t != null) { q1.add(t); } while (!q1.isEmpty()) { node t1 = q1.poll(); if (t1.left != null) q1.add(t1.left); if (t1.right != null) q1.add(t1.right); System.out.print(t1.value + " "); } System.out.println(); }
前中後序遍歷(遞迴)
其實這種就是一個類似dfs的思想。用遞迴實現。前面有很詳細的介紹遞迴演算法。我們採用的三序遍歷是採用同一個遞迴。並且大家也都直到遞迴是一個有來有回的過程。三序遍歷只是利用了遞迴中的來回過程中不同片段擷取輸出,而達到前(中、後序遍歷的結果)。
前序遞迴
前序的規則就是根結點 ---> 左子樹 ---> 右子樹.我們在呼叫遞迴前進行節點操作。對於前序,就是先訪問(輸出)該節點。而遞迴左,遞迴右側,會優先遞迴左側。直到沒有左節點。才會停止。訪問次序大致為: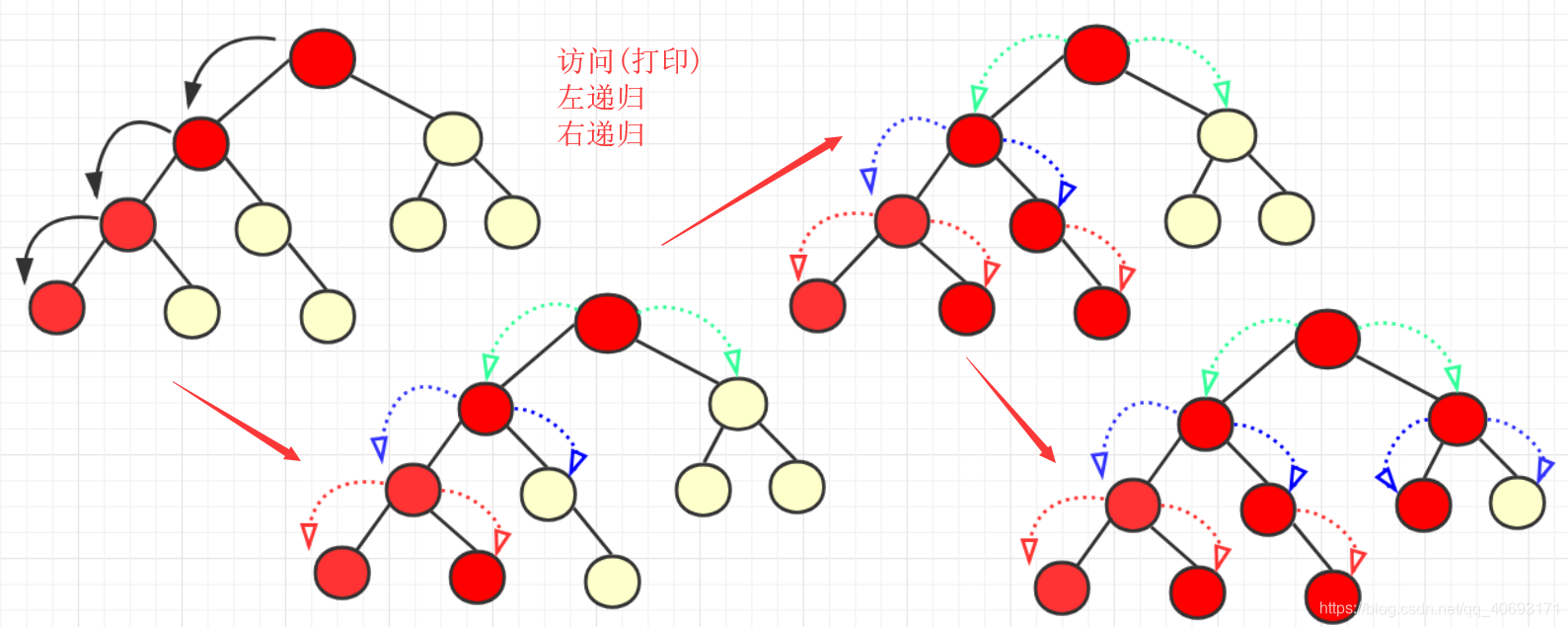
public void qianxu(node t)// 前序遞迴 前序遍歷:根結點 ---> 左子樹 ---> 右子樹 { if (t != null) { System.out.print(t.value + " ");// 當前節點 qianxu(t.left); qianxu(t.right); } }
中序遞迴
有了前序的經驗,我們就很好利用遞迴實現中序遍歷。中序遍歷的規則是:左子樹---> 根結點 ---> 右子樹。所以我們訪問節點的順序需要變。
- 我們直到遞迴是
來回的過程,對於恰好有兩個子節點(子節點無節點)的節點來說。只需要訪問一次左節點,訪問根,訪問右節點。即可。 - 而如果兩側有節點來說。每個節點都要滿足中序遍歷的規則。我們從根先訪問左節點。到了左節點這兒左節點又變成
一顆子樹,也要滿足中序遍歷要求。所以就要先訪問左節點的左節點(如果存在)。那麼如果你這樣想,規則雖然懂了。但是也太複雜了。那麼我們藉助遞迴。因為它的子問題和根節點的問題一致,只是範圍減小了。所以我們使用遞迴思想來解決。 - 那麼遞迴的邏輯為:考慮特殊情況(特殊就直接訪問)不進行遞迴否則遞迴的訪問左子樹(讓左子樹執行相同函式,特殊就停止遞迴輸出,不特殊就一直找下去直到最左側節點。)——>輸出該節點—>遞迴的訪問右子樹.
程式碼為:
public void zhongxu(node t)// 中序遍歷 中序遍歷:左子樹---> 根結點 ---> 右子樹
{
if (t != null) {
zhongxu(t.left);
System.out.print(t.value + " ");// 訪問完左節點訪問當前節點
zhongxu(t.right);
}
}
後序遞迴
同理,有了前面的分析,後續就是左子樹 ---> 右子樹 ---> 根結點
public void houxu(node t)// 後序遍歷 後序遍歷:左子樹 ---> 右子樹 ---> 根結點
{
if (t != null) {
houxu(t.left);
houxu(t.right);
System.out.print(t.value + " "); // 訪問玩左右訪問當前節點
}
}
非遞迴前序
法一(技巧)
- 非遞迴的前序。我們利用棧的性質替代遞迴,因為
遞迴有時候在效率方面不是令人滿意的。
利用棧,我們直到棧的順序為現金先出。那麼順序如何新增?遞迴是左遞迴,右遞迴。但是利用棧要相反,因為如果左進棧、右進棧會出現以下後果: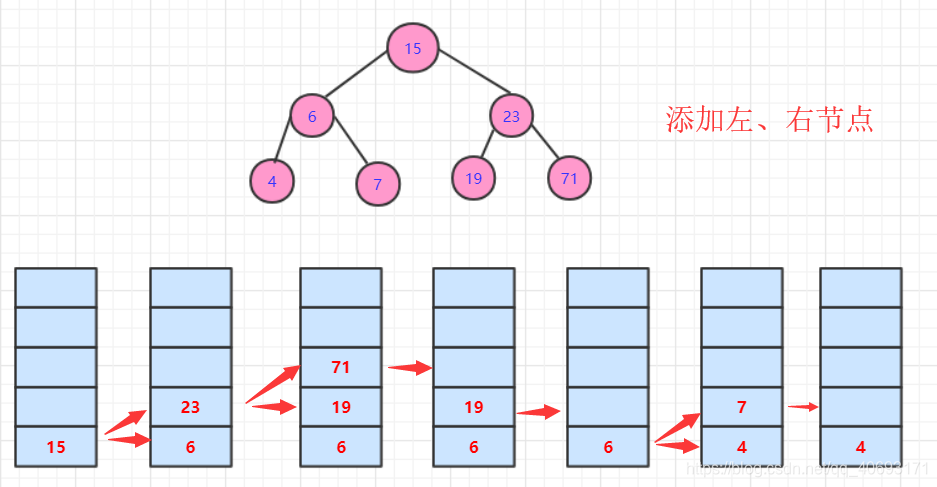
所以,我們要利用遞迴的思路,需要先放右節點進棧,再放左節點進棧,這個下次·再取節點取到左節點·,這個節點再右節點進棧,左節點進棧。然後迴圈一直到最後會一直優先取到左節點。達到和遞迴順序相仿效果。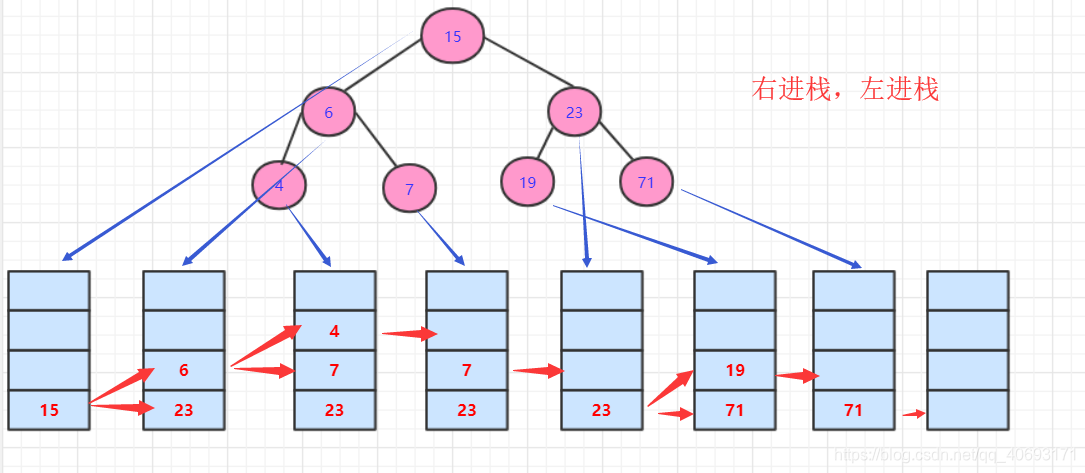
每pop完新增右左節點直接輸出(訪問)即可完成前序非遞迴遍歷。
public void qianxu3(node t)// 非遞迴前序 棧 先左後右 t一般為root
{
Stack<node> q1 = new Stack<node>();
if (t == null)
return;
if (t != null) {
q1.push(t);
}
while (!q1.empty()) {
node t1 = q1.pop();
if (t1.right != null) {
q1.push(t1.right);
}
if (t1.left != null) {
q1.push(t1.left);
}
System.out.print(t1.value + " ");
}
}
法二(傳統)
方法二和非遞迴中序遍歷的方法類似,只不過需要修改輸出時間,在進棧時候輸入訪問節點即可。具體參考中序遍歷分析。
public void qianxu2(node t) {
Stack<node> q1 = new Stack();
while(!q1.isEmpty()||t!=null)
{
if (t!=null) {
System.out.print(t.value+" ");
q1.push(t);
t=t.left;
}
else {
t=q1.pop();
t=t.right;
}
}
}
非遞迴中序
非遞迴中序和前序有所區別。
我們直到中序排列的順序是:左節點,根節點,右節點。那麼我們在經過根節點的前面節點 不能釋放, 因為後面還需要用到它。所以要用棧先儲存。
它的規則大致為:
- 棧
依次存入左節點所有點,直到最左側在棧頂。 - 開始
丟擲棧頂並訪問。(例如第一個丟擲2)。如果有右節點。那麼將右節點加入棧中,然後右節點一致左下遍歷直到尾部。(這裡5和7沒有左節點,所以不加)但是如果丟擲15。右節點加入23.再找23的左側節點加入棧頂。就這樣迴圈下去直到棧為空。
可行性分析:中序是左—中—右的順序。訪問完左側。當丟擲當前點的時候說明左側已經訪問完(或者自己就是左側),那麼需要首先訪問當前點的右側。那麼這個右節點把它當成根節點重複相同操作(因為右節點要滿足先左再右的順序)。這樣其實就是模擬了一個遞迴的過程,需要自己思考。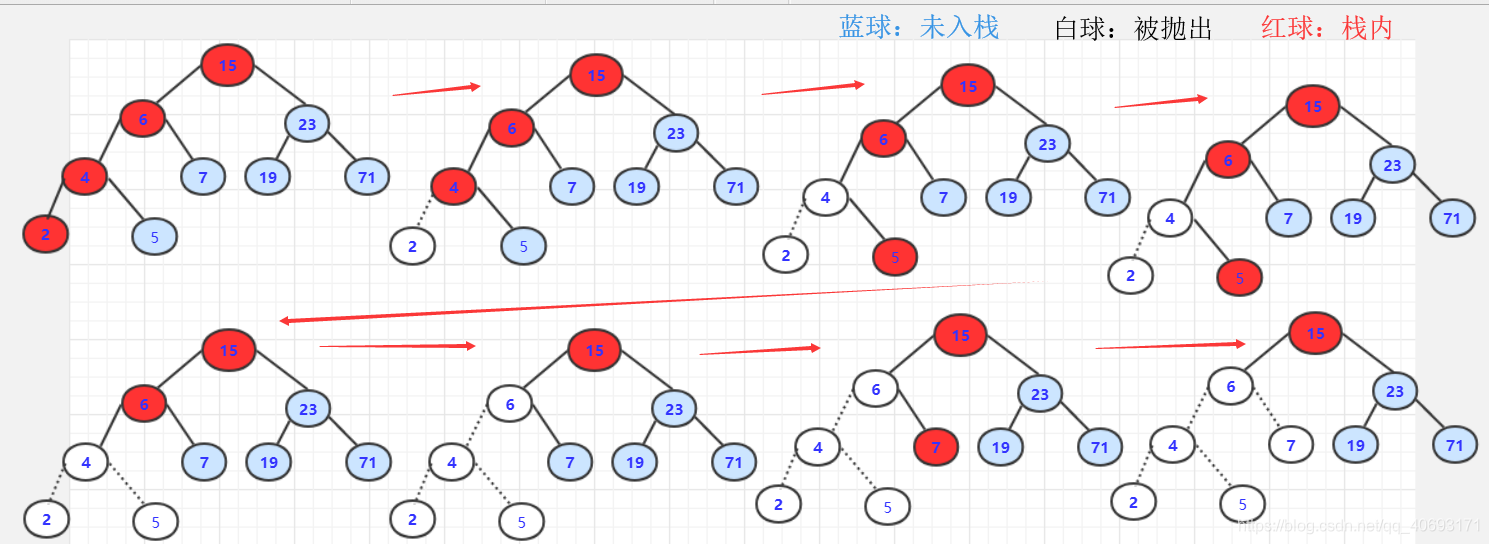
實現程式碼1:
public void zhongxu2(node t) {
Stack<node> q1 = new Stack();
while(!q1.isEmpty()||t!=null)
{
if (t!=null) {
q1.push(t);
t=t.left;
}
else {
t=q1.pop();
System.out.print(t.value+" ");
t=t.right;
}
}
}
實現程式碼2:(個人首次寫的)
public void zhongxu3(node t)// 先儲藏所有左側點,丟擲一個點,訪問該點右節點,對右節點在儲存所有子左節點
{
Stack<node> q1 = new Stack();
if (t == null)
return;
if (t != null) {
q1.push(t);
}
node t1 = q1.peek();// 不能丟擲,要先存最左側
while (t1.left != null) {
t1 = t1.left;
q1.push(t1);
}
while (!q1.isEmpty()) {
node t2 = q1.pop();
System.out.print(t2.value + " ");
if (t2.right != null) {
t2 = t2.right;
q1.push(t2);
while (t2.left != null) {
t2 = t2.left;
q1.push(t2);
}
}
}
}
非遞迴後序※
非遞迴後序遍歷有兩種方法
一種方法是利用和前面中序、前序第二種方法類似的方法進入壓棧出棧,但是要藉助額外的標記次數,一個節點訪問第二次才能輸出。(這個訪問第一次是入棧,第二次是子樹解決完畢自己即將出棧(先不出棧))。
法1(傳統方法)
在前面的前序和中序先到最左側壓入棧的時候,兩種順序依次是
- 前序:
中入棧——>左入棧——>左出棧——>中出棧——>右入棧——>右孩子入出——>右出棧 在入棧時候操作即可前序 - 中序: 中入棧——>左入棧——>
左出棧——>中出棧——>右入棧 ——>右孩子入出——>右出棧按照出棧順序即可完成中序
而在後序遍歷中:它有這樣的規則:
- 入棧,第一次訪問
即將出棧。第二次訪問,- 如果有右孩子,先不出棧把右孩子壓入棧第一次訪問,如果沒右孩子。訪問從棧中彈出。
- 迴圈重複,直到棧為空
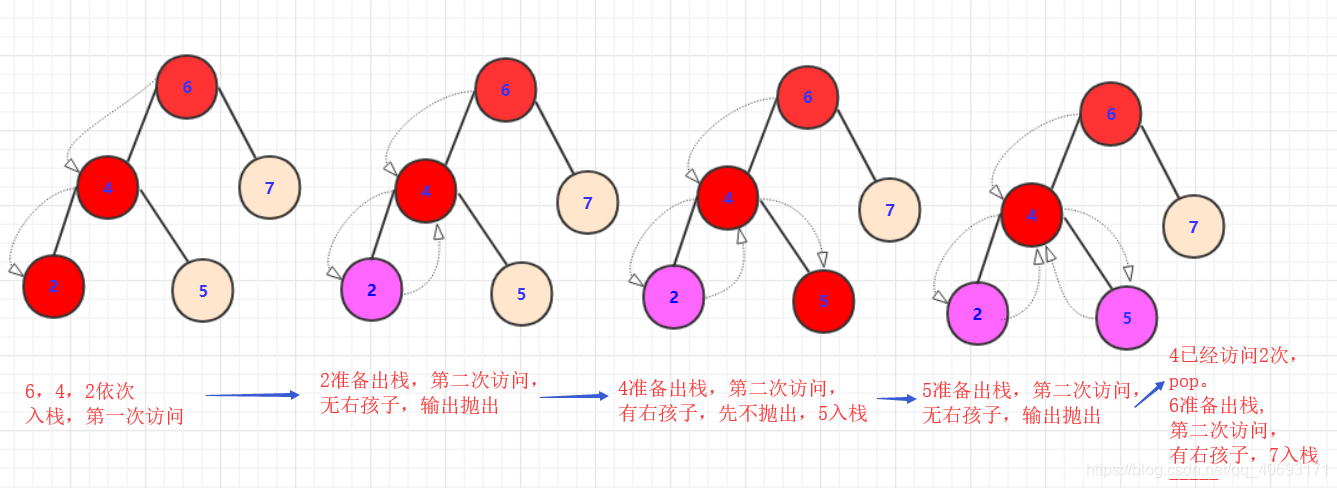
實現程式碼為(用map記錄節點出現次數):
public void houxu2(node t) {
Stack<node> q1 = new Stack();
Map<Integer,Integer >map=new HashMap<>();
while(!q1.isEmpty()||t!=null)
{
if (t!=null) {
q1.push(t);
map.put(t.value, 1); //t.value標記這個值節點出現的次數
t=t.left;
}
else {
t=q1.peek();
if(map.get(t.value)==2) {//第二次訪問,丟擲
q1.pop();
System.out.print(t.value+" ");
t=null;//需要往上走
}
else {
map.put(t.value, 2);
t=t.right;
}
}
}
}
法2(雙棧):
另一種方法是藉助雙棧進行處理。我們曾在前序方法一藉助一個棧右壓,左壓。持續讓達到一個前序遍歷的效果。但是這個方法很難實現後續。
- 分析相同方法,如果我們
先壓左,再壓右,那麼我們獲得的順序將是和前序完全相反的順序(順序為:中間,右側,左側。倒過來剛好是左側、右側、中間的後續)對稱看起來的前序。即用另一個棧將序列進行反轉順序!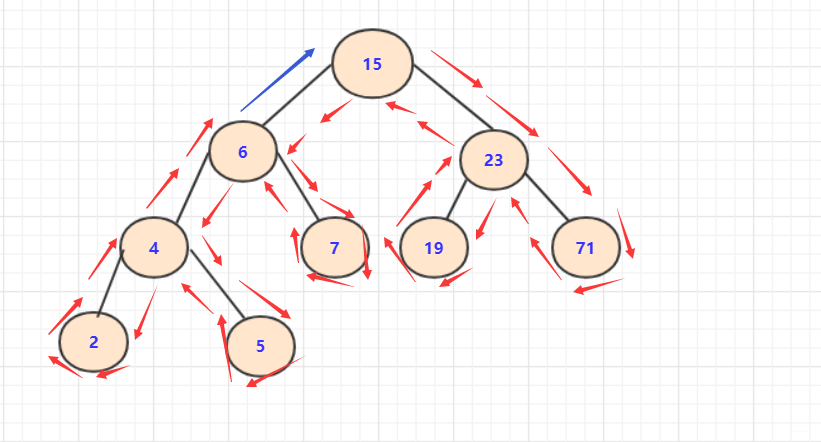
如果再這個過程,我們利用另一個棧進行儲存,將它的首次入棧用一個棧存入,相當於起到一個反轉的作用。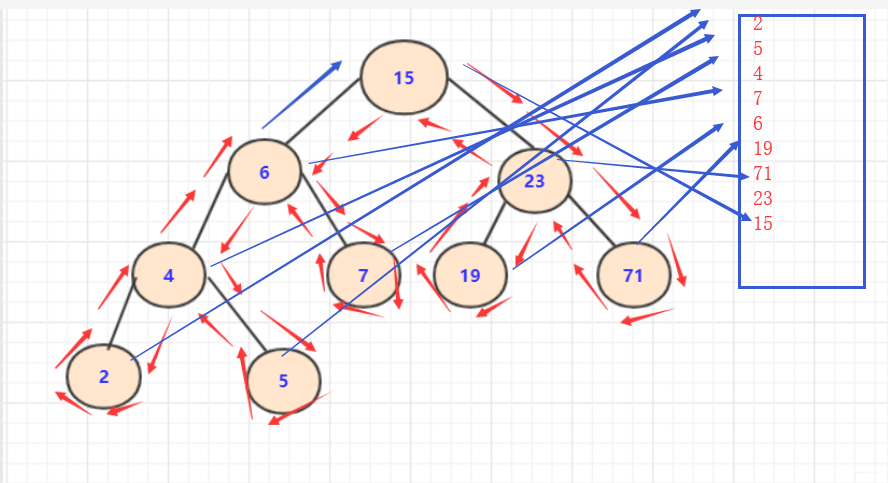
實現程式碼為:
public void houxu3(node t)// q1和q2 q1要先右後左,先遍歷右側,q1先裝右側就把右側放到前面,左側放在上面(棧頂)
{
Stack<node> q1 = new Stack();
Stack<node> q2 = new Stack();
if (t == null)
return;
if (t != null) {
q1.push(t);
}
while (!q1.isEmpty()) {
node t1 = q1.pop();
q2.push(t1);
if (t1.left != null) {
q1.push(t1.left);
}
if (t1.right != null) {
q1.push(t1.right);
}
}
while (!q2.isEmpty()) {
node t1 = q2.pop();
System.out.print(t1.value + " ");
}
}
總結
測試結果: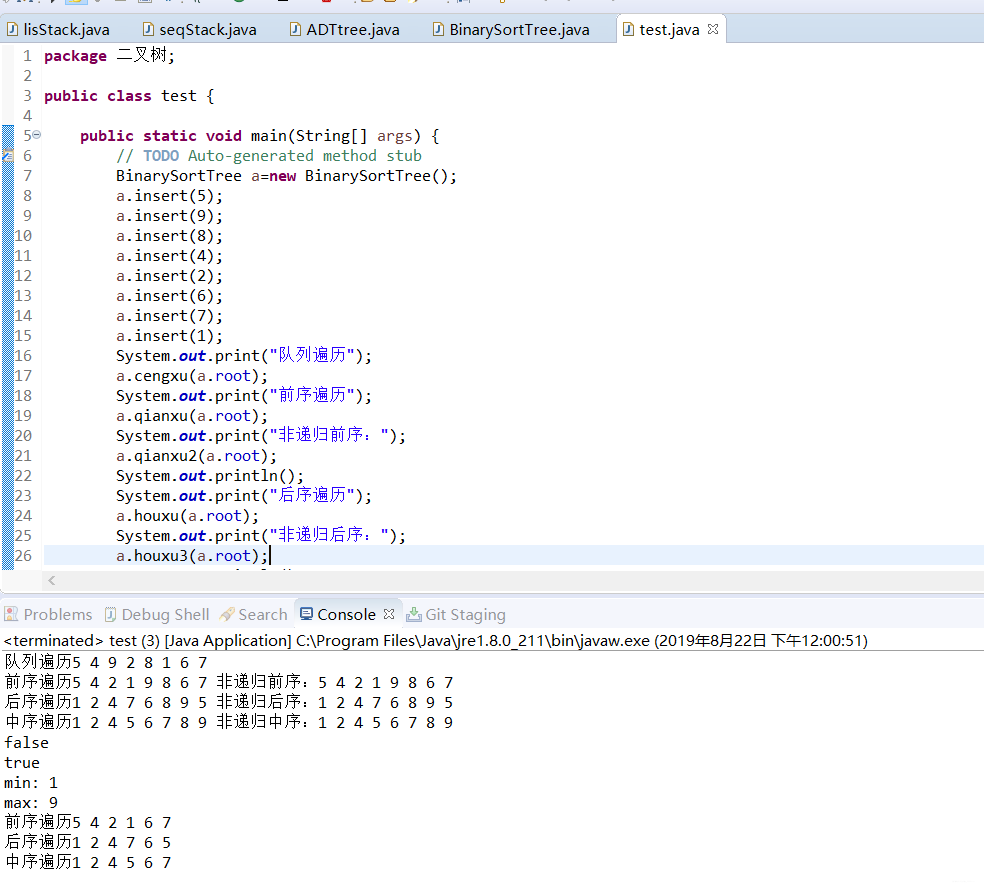
這部分內容比較多,也可能比較雜,希望大家好好吸收,也可能筆者寫的大意或者錯誤。還請大佬指正。!
- 另外,完整程式碼還請關注公眾號(
bigsai)。筆者認真更新資料結構與演算法。有興趣可以關注一波學一起學習。回覆資料結構或者爬蟲有精心準備學習資料贈送。
