資訊基礎II | Homework 1
目錄
一、什麼叫做線性賦範空間
1. 距離:
2. 線性空間:
- 有向量的加法和數乘
- 滿足:
向量加法結合律:u + (v + w) = (u + v) + w;
向量加法交換律:v + w = w + v;
向量加法的單位元:V 裡有一個叫做零向量的 0,∀ v ∈ V , v + 0 = v;
向量加法的逆元素:∀v∈V, ∃w∈V,使得 v + w = 0;
標量乘法分配於向量加法上:a(v + w) = a v + a w;
標量乘法分配於域加法上: (a + b)v = a v + b v;
標量乘法一致於標量的域乘法: a(b v) = (ab)v;
標量乘法有單位元: 1 v = v, 這裡 1 是指域 F 的乘法單位元。
3. 定義範數

賦予範數或者距離的幾何分別稱為:賦範空間和度量空間;
若在其上再加上線性結構稱為線性賦範空間和線性度量空間。
二、圖的定義
圖(Graph)是由頂點的有窮非空集合和頂點之間的集合組成,通常表示為:G(V, E),其中 G 表示一個圖,V 是圖 G 中頂點的集合,E 是圖 G 中邊的集合。
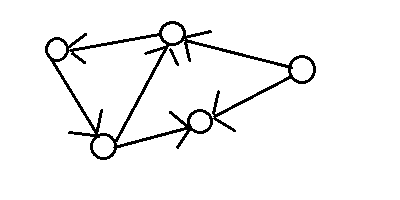
圖的表示:一般使用圓圈表示頂點,使用線段表示邊,一條邊連線兩個不同的頂點。有些邊是帶方向的稱為有向邊,當頂點v到u含有一條有向邊,就畫一個箭頭從v指向u,使用元組(v,u)表示;而沒有方向的邊稱為無向邊,當頂點v到u含有一條有向邊,就畫一條線段從v指向u,使用元組(v,u)表示。例如下面分別是有向圖
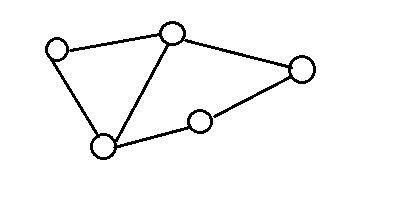
有向圖 無向圖
圖根據邊的分類分為有向圖和無向圖,有向圖的邊是有向邊,它就像公路的單行道一樣,只能從一個方向到另一個方向。無向圖的邊是無向邊,當然它就像雙向車道一樣可以互相到達,而且兩個頂點是沒有區別的。
當且僅當(u,v)是圖的邊,稱頂點v和u是鄰接的。邊(u,v)關聯於頂點u和v。對於無向圖這種鄰接和關聯是對等的,而有向圖是單向的,它僅僅從u到v。
權:在圖的一些應用中,可能要為每條邊賦予一個表示大小的值,這個值就稱為權。例如從城市A到城市B存在一條公路,而可以使用權表示這條公路的距離。
路徑:一個頂點序列i1,i2........ik是圖的一條路徑,當且僅當邊(i1,i2)(i2,i3).........(ik-1,ik)都在圖中。如果除了第一個頂點和最後一個頂點之外,其餘的頂點均不相同,那麼這條路徑稱為簡單路徑。
連通圖:設圖G是無向圖,當且僅當G的每一對頂點之間都有一條路徑,則稱G是連通圖。
子圖:如果圖H的頂點和邊的集合是圖G的子集,那麼稱圖H是圖G的子圖。
生成樹:如果圖H是圖G的子圖,且他們的頂點集合相同,並且H是沒有環路的無向連通圖(即一棵樹),則稱H是G的一棵生成樹。
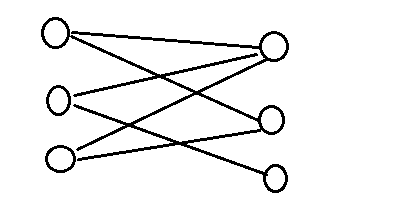
二分圖:圖G的頂點被分為兩個子集,而且每條邊只能從一個子集到另一個子集。例如:
強連通圖:圖G是一個有向圖,當且僅當每一對不同的頂點u,v,從u到v和v到u都有一條有向路徑。
三、啟用函式
1. 筆記
sigmoid [維基百科]
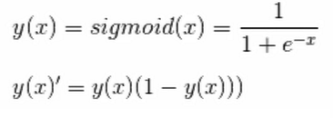
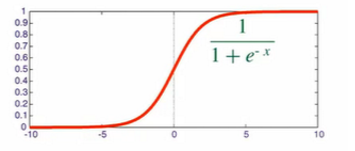
tanh [維基百科]

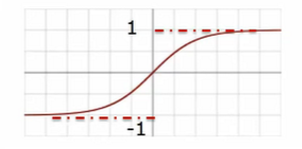
ReLU [維基百科]

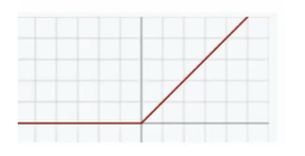
正向截斷負值,損失大量特徵(特徵足夠多,所以即使截斷80%後還能用)
反向梯度沒有損失
Leaky ReLU [維基百科]

更加有效率的梯度下降以及反向傳播:避免了梯度爆炸和梯度消失問題。
簡化計算過程:沒有了其他複雜啟用函式中諸如指數函式的影響;同時活躍度的分散性使得神經網路整體計算成本下降。
2. 維基百科
這裡我貼上了維基百科上關於啟用函式的各種型別的介紹,如下所示:



3. Feisky
四、R^n的緊緻子集
設(X, ρ)是一個度量空間,A ∈ X,如果存在實數M>0使得ρ(x, y)<M對於所有的x, y∈A成立,則稱A是X的一個有界子集;如果X本身是一個有界子集,則稱度量空間(X, ρ)是一個 有界度量空間。
緊緻度量空間是有界的。
度量空間的每個緊緻子集都是有界子集
一個直觀一點的理解,幾個集合是“緊”的,就是說,無限個點撒進去,不可能充分散開。無論鄰域多麼小,必然有一些鄰域裡面有無限個點。上面關於 compactness的這個定義的玄機就在有限和無限的轉換中。一個緊的集合,被無限多的小鄰域覆蓋著,但是,總能找到其中的有限個就能蓋全。那麼,後果是什麼呢?無限個點撒進去,總有一個鄰域包著無數個點。鄰域們再怎麼小都是這樣——這就保證了無限序列中存在極限點。
五、《無限逼近理論》閱讀
維基百科:Universal approximation theorem
六、x1 ~ x6,n1 ~ n9,y1 ~ y4,寫輸出公式