20172330 2018-2019-1 《程式設計與資料結構》第九周學習總結
20172330 2018-2019-1 《程式設計與資料結構》第九周學習總結
教材學習內容總結
一、無向圖:
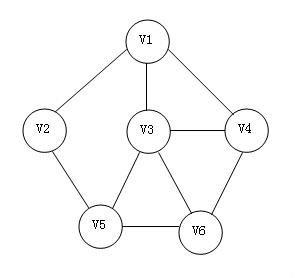
邊沒有方向的圖稱為無向圖。
- 無向圖中,表示邊的頂點對是無序的,例如,標記頂點A,B,C,D,一條邊可以表示為(A,B)。無向圖表示頂點對是無序的,所以邊(A,B)意味著A和B之間的連線是雙向的,在一個無向圖中,(A,B)和(B,A)所代表的邊的含義完全一樣。
含有最多條邊的無向圖稱為完全圖:Edges=(n-1)*n/2.

- 如果無向圖中任意兩個頂點間都有路徑,則無向圖稱為連通的。
- 路徑是連線圖中兩個頂點的邊的序列,路徑長度為路徑所含邊的數目(頂點個數減一)
- 第一個頂點和最後一個頂點是同一個頂點且沒有重複邊的路徑,稱為一個環。
如果圖中兩個頂點之間有邊連線,則稱這兩個頂點是鄰接的(鄰居),自己連線到自己的邊稱為自迴圈或懸掛。
二、有向圖
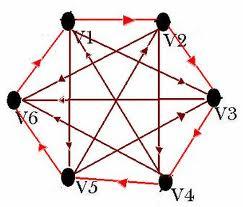
如果給圖的每條邊規定一個方向,那麼得到的圖稱為有向圖,其邊也稱為有向邊。在有向圖中,與一個節點相關聯的邊有出邊和入邊之分,而與一個有向邊關聯的兩個點也有始點和終點之分。
- 頂點是有序對的圖稱為有向圖,有向圖的每條邊都帶有一個移動方向,這個方向有頂點的順序指定,所以(A,B)表示只允許從A移動到B,但不允許另一個方向的移動。
- 樹就是圖,樹的大部分工作是針對有向樹。有向樹是一個有向圖。
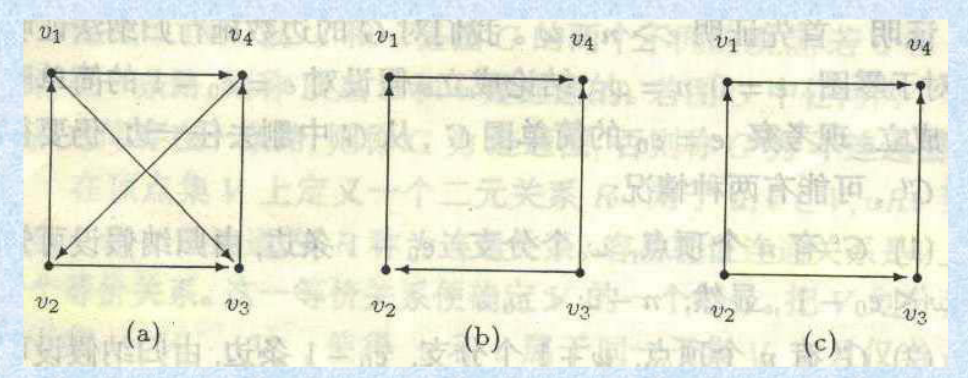
如上圖:a是強連通,b是單向連通,c是弱連通。
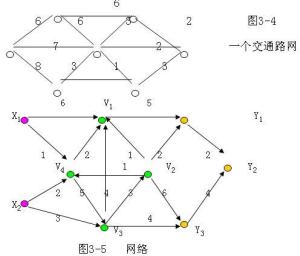
三、網路
- 網路是一種圖,一般認為它專指加權圖,是一種每條邊都帶有權重或代價的圖。
四、常用的圖演算法
遍歷
1.深度優先遍歷
首先從圖中某個頂點v0出發,訪問此頂點,然後依次從v0相鄰的頂點出發深度優先遍歷,直至圖中所有與v0路徑相通的頂點都被訪問了;若此時尚有頂點未被訪問,則從中選一個頂點作為起始點,重複上述過程,直到所有的頂點都被訪問。可以看出深度優先遍歷是一個遞迴的過程。
2.廣度優先遍歷
首先,從圖的某個頂點v0出發,訪問了v0之後,依次訪問與v0相鄰的未被訪問的頂點,然後分別從這些頂點出發,廣度優先遍歷,直至所有的頂點都被訪問完。最小生成樹
1.一個連通圖的生成樹是一個極小的連通子圖,它含有圖中全部的頂點,但只有足以構成一棵樹的n-1條邊。我們把構造連通網的最小代價生成樹。稱為最小生成樹。其邊的權重總和小於或等於同一個圖中其他任何一棵生成樹的權重總和。
2.Prim演算法:先以一個結點作為最小生成樹的第一個結點,然後以迭代的方式找出與最小生成樹中各結點權值最小邊,加到最小生成樹中。加入之後如果產生迴路則跳過這條邊,選擇下一個結點。當所有結點都加入到最小生成樹中之後,就找出最小生成樹了。

五、圖的實現策略
- 鄰接表
因為樹就是圖,所以實現圖的最好方式也許是採用實現樹已用過的機制。使用一組結點,每個結點包含一個元素及可能和連結其他結點的一個連結串列。
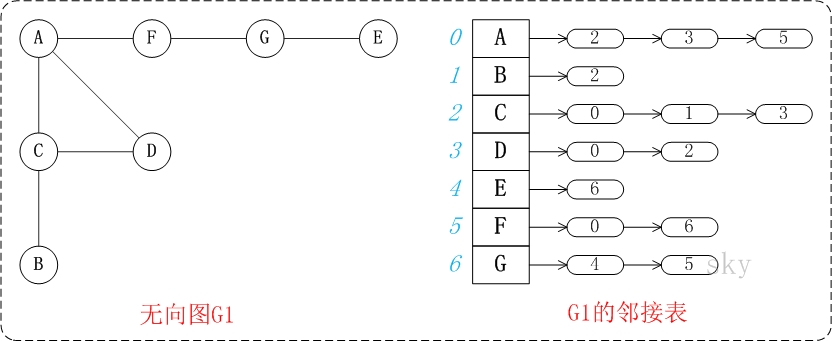
- 鄰接矩陣
用一個一維陣列存放圖中所有頂點資料;用一個二維陣列存放頂點間關係(邊或弧)的資料,這個二維陣列稱為鄰接矩陣。用鄰接矩陣表示圖,很容易確定圖中任意兩個頂點是否有邊相連。鄰接矩陣分為有向圖鄰接矩陣和無向圖鄰接矩陣。對無向圖(無向簡單圖)而言,鄰接矩陣一定是對稱的,而且對角線一定為零,有向圖則不一定如此。
教材學習中的問題和解決過程
- 問題1:圖的遍歷與樹的遍歷有什麼區別?
問題1解決方案:樹是有序的,圖是無序的。圖有兩種林子裡的方法,一種是廣度優先遍歷,另一種是深度優先遍歷。對於樹來說,它的廣度優先遍歷就是層序遍歷,深度優先遍歷就是先序遍歷。
- 問題2:鄰接矩陣有向圖與無向圖的對比?
問題2解決方案:
因為無向圖不需要表示整個矩陣,只需給出矩陣對角線的一側,而有向圖的所有邊都是定向的,所以結果對應並不相同:
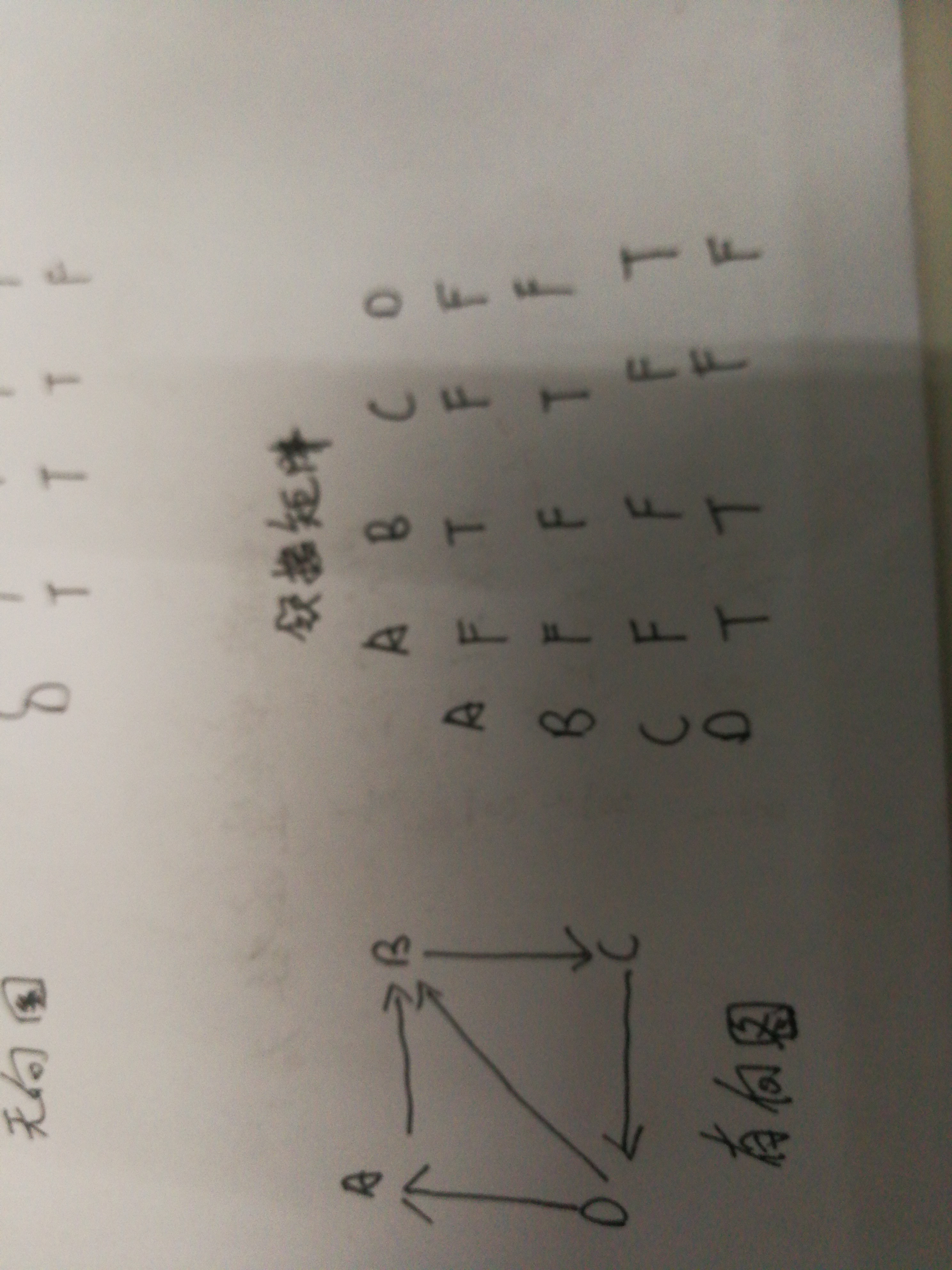

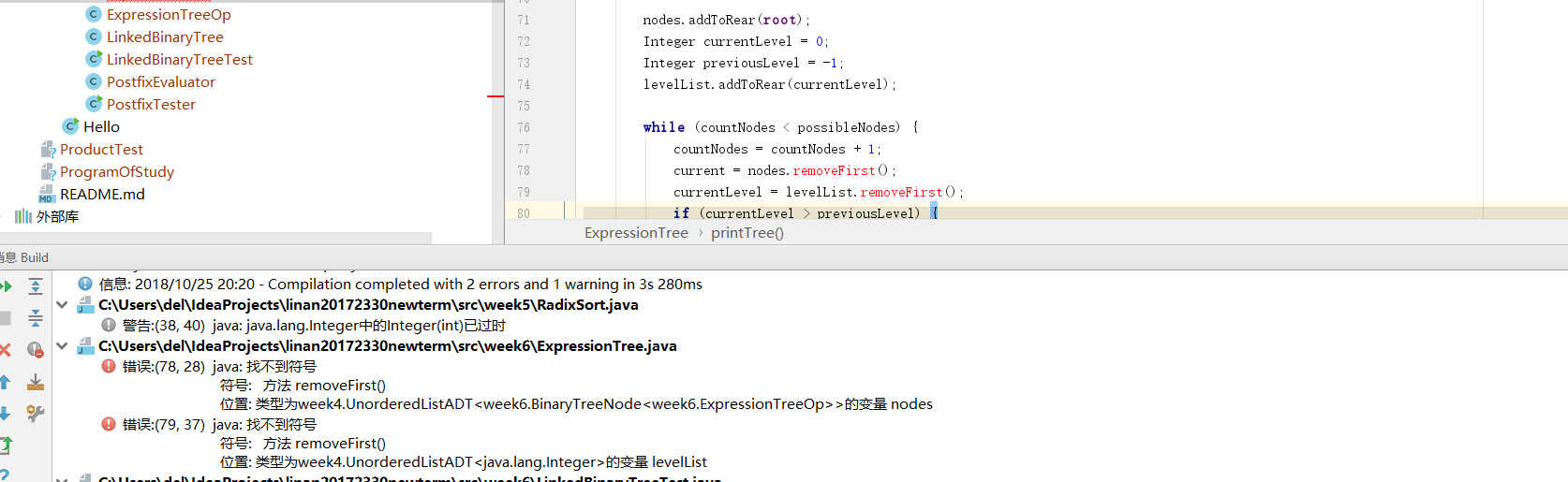
程式碼除錯中的問題和解決過程
- 問題1:在編寫樹的方法時,RemoveFirst方法一直報錯
- 問題1解決方案:在檢查後發現是在ListADT時沒有寫進去導致出現了錯誤。
程式碼託管

上週考試錯題總結
- Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
A .True
B .Flase
解析:
堆是一棵完全二叉樹、不是一顆二叉搜尋樹。
結對及互評
- 基於評分標準,我給嚴域俊的部落格打分:7分。得分情況如下:
正確使用Markdown語法(加1分)
模板中的要素齊全(加1分)
教材學習中的問題和解決過程, (加3分)
感想,體會真切的(加1分)
點評認真,能指出部落格和程式碼中的問題的(加1分)
- 部落格中值得學習的或問題:
- 圖片和文字相結合,方便理解。
- 增加了部落格中的目錄,方便檢視,同時樣式進行了更新,顯得更加美觀
- 閱讀了許多資料,使得部落格更有說服力。
- 程式碼中值得學習的或問題:
- commit依舊很詳細,有條理性。
點評過的同學部落格和程式碼
- 本週結對學習情況
- 20172333
- 結對學習內容
教材第11章,執行教材上的程式碼
完成課後自測題,並參考答案學習
完成課後自測題,並參考答案學習
完成程式設計專案:至少完成PP11.3、PP11.8
其他(感悟、思考等,可選)
這一週花了點心思在這一章上面,也好好閱讀了很多內容,掌握的還算可以。
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 0/0 | 1/1 | 10/10 | |
| 第二週 | 700/700 | 1/2 | 10/20 | |
| 第三週 | 700/1400 | 1/3 | 10/30 | |
| 第四周 | 500/1900 | 2/5 | 10/40 | |
| 第五週 | 569/2469 | 1/6 | 10/50 | |
| 第六週 | 1070/3539 | 1/7 | 10/60 | |
| 第七週 | 986/4625 | 1/8 | 10/70 | |
| 第八週 | 1023/5648 | 2/10 | 10/80 | |
| 第九周 | 1023/6967 | 1/11 | 10/90 |
計劃學習時間:10小時
實際學習時間:10小時
