20172306 2018-2019-2 《Java程式設計與資料結構》第九周學習總結
20172306 2018-2019-2 《Java程式設計與資料結構》第九周學習總結
教材學習內容總結
- 無向圖
圖是由結點和這些結點之間的連線構成

- 就圖來說,結點叫做頂點,結點之間的連線是邊,一般用名字或標籤來表示頂點。
- 無序圖是一種邊為無序結點對的圖,如果圖中的兩個頂點之間有一條連通邊,則稱為這兩個頂點是鄰接的,鄰接頂點有時也稱為鄰居,連通一個頂點及其自身的邊稱為自迴圈或環。
- 路徑是圖中的一系列邊,每條邊連通兩個頂點。路徑的長度是該路徑中邊的條數(或者是頂點數減去1)
- 樹是圖的一種。
如果無向圖中任意兩個頂點之間都存在一條路徑,則認為這個無向圖是連通的。

- 如果無向圖擁有最大數目的連通頂點的邊,則認為這個無向圖是完全的。對有n個頂點的無向圖,要使該圖為完全的,要求有n(n-1)/2條邊(假設其中沒有邊是自迴圈的)
- 對於這個n(n-1)/2這個值的由來:
- 對於圖來說,第一個頂點最多有(n-1)條邊和其他結點相連,第二個頂點最多有(n-2)條邊和其他結點相連,以此類推,那最後如果要是圖是完全的,就需要(n-1)+(n-2)+(n-3)+...+3+2+1,最後它們求和結果就是n(n-1)/2。
- 對於這個n(n-1)/2這個值的由來:
- 環路是一種首項點和末項點相同且沒有重邊的路徑。沒有環路的圖稱為無環的。
無向樹是一種連通的無環無向圖,其中一個元素被指定為樹根。
- 有向圖
- 有向圖有時也稱為雙向圖,它是一種邊為有序頂點對的圖
- 有向圖連通的例子:
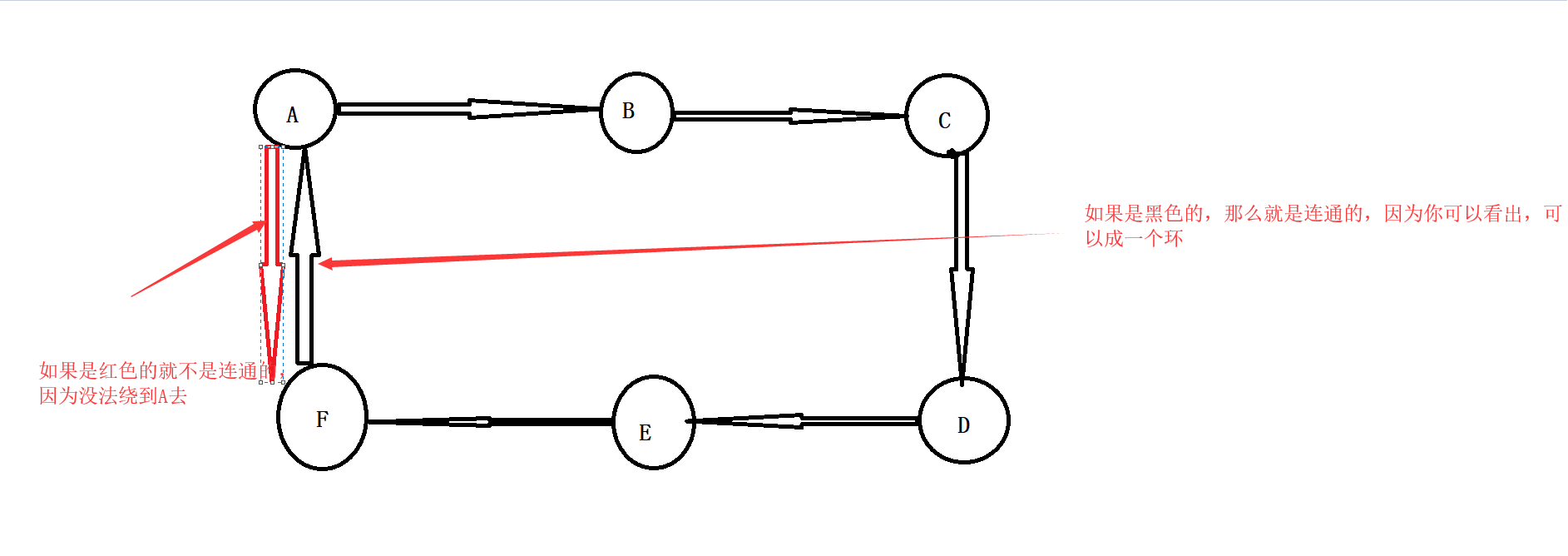
- 如果有向圖中沒有環路,且有一條從A到B的邊,則可以把頂點A安排在頂點B之前,這種排列得到的頂點次序稱為拓撲序
- 有向樹是一種指定了一個元素作為樹根的有向圖,該圖還有如下屬性:
- 不存在其他頂點到樹根的連線
- 每個非樹根元素恰好有一個連線
- 樹根到每個其他頂點都有一條路徑
- 網路
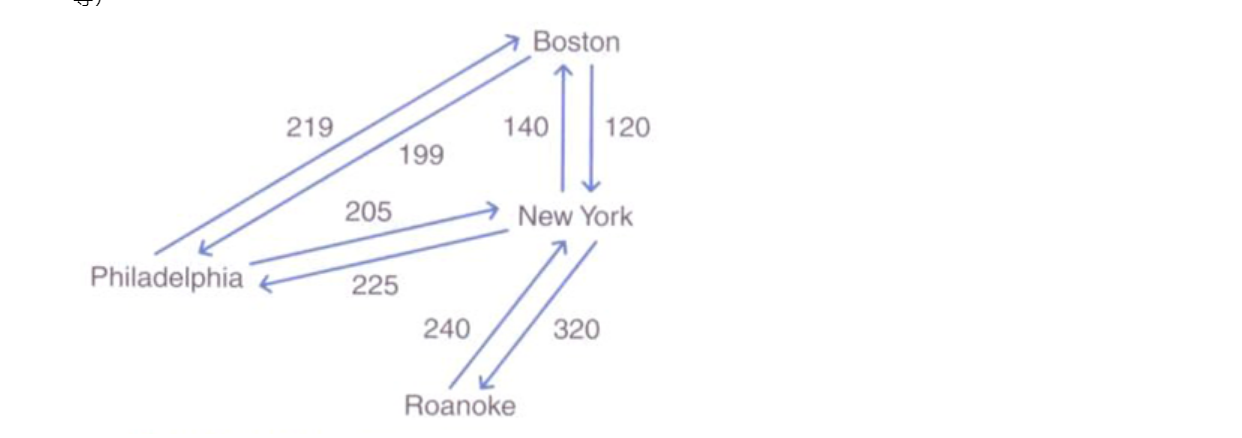
- 網路或稱為加權圖,是一種每條邊都帶有權重或代價的圖,加權圖中的路徑權重是該路徑中各條邊權重的和。
- 對於網路,我們將用一個三元組來表示每條邊,這個三元組中包括起始頂點、終止頂點和權重。對於無向網路來說,起始頂點與終止頂點可以互換。
- 常用的圖演算法
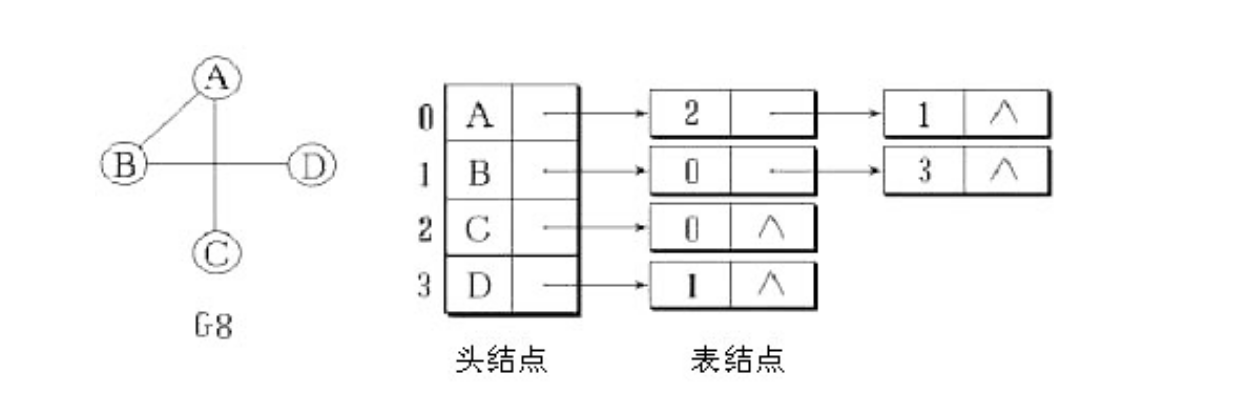
- 我們在進行圖的儲存結構的時候有兩種方式:
一種是利用基於二維陣列的鄰接矩陣表示法

一種就是基於連結串列的的鄰接表
- 遍歷有兩種:廣度優先遍歷和深度優先遍歷(圖的遍歷和樹的遍歷有一點不同是:圖中不存在根結點,所以圖的遍歷可以從其中的任一頂點開始)
- 廣度優先遍歷(類似於樹的層次遍歷)這是一個對於廣度優先遍歷的一個很詳細很詳細的過程
- (1)利用佇列管理遍歷;利用無序列表構造出結果。
- (2)起始頂點進入佇列,同時標記該頂點為已訪問的
- (3)在迴圈中,從佇列中取出首頂點然後新增到列表的末端
- (4)所有與當前頂點鄰接的尚未被標記的依次進入佇列並被標記,然後再進入列表中
- (5)重複上面的迴圈,直到佇列為空
- 就廣度優先遍歷,舉一個例子:
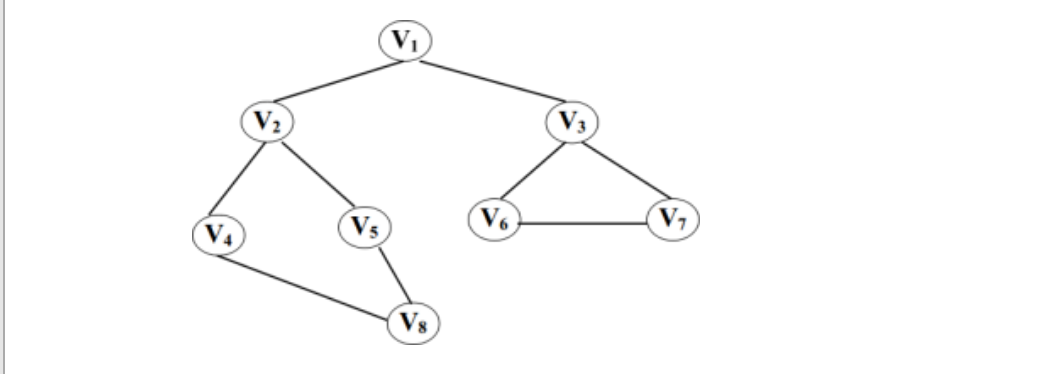
- 就該圖而言,走一下廣度優先遍歷的過程:
- a.將V1加入佇列,取出V1,並標記為true(即已經訪問),然後從佇列中將V1取出,放進列表的末端。
- b. 將其鄰接點加進入佇列,則 <—[V2 V3],並標記為true(即已經訪問),從佇列取出V2,放進列表中。
- c.將其未訪問過的鄰接點加進入佇列,則 <—[V4 V5],並標記為true(即已經訪問),取出V3,放進列表中。
- d.將其未訪問過的鄰接點加進入佇列,則 <—[V6 V7],並標記為true(即已經訪問),取出V4,放進列表中。
- e.將其未訪問過的鄰接點加進入佇列,則 <—[V8],並標記為true(即已經訪問),取出V5,放進列表中,
- f.因為其鄰接點已經加入佇列,則 <—[ ],取出V6,放進列表中。
- g.取出V7,放進列表中。
- h.取出V8,放進列表中。
- i.遍歷結束
- 就該圖而言,走一下廣度優先遍歷的過程:
- 我們在進行圖的儲存結構的時候有兩種方式:
該例子是無向圖而言的,但和有向圖是很像的
- 深度優先遍歷(類似於樹的前序遍歷)
- (1)利用棧管理遍歷,利用無序列表構造出結果
- (2)起始頂點進入棧,同時標記該頂點為已訪問的
- (3)在迴圈中,從棧中取出首頂點新增到列表的末端
- (4)所有與當前頂點鄰接的尚未被標記的依次進入棧中,然後再從棧中取出進入列表,之後被標記
- (5)重複上面的迴圈,直到佇列為空
就深度優先遍歷,舉一個例子:
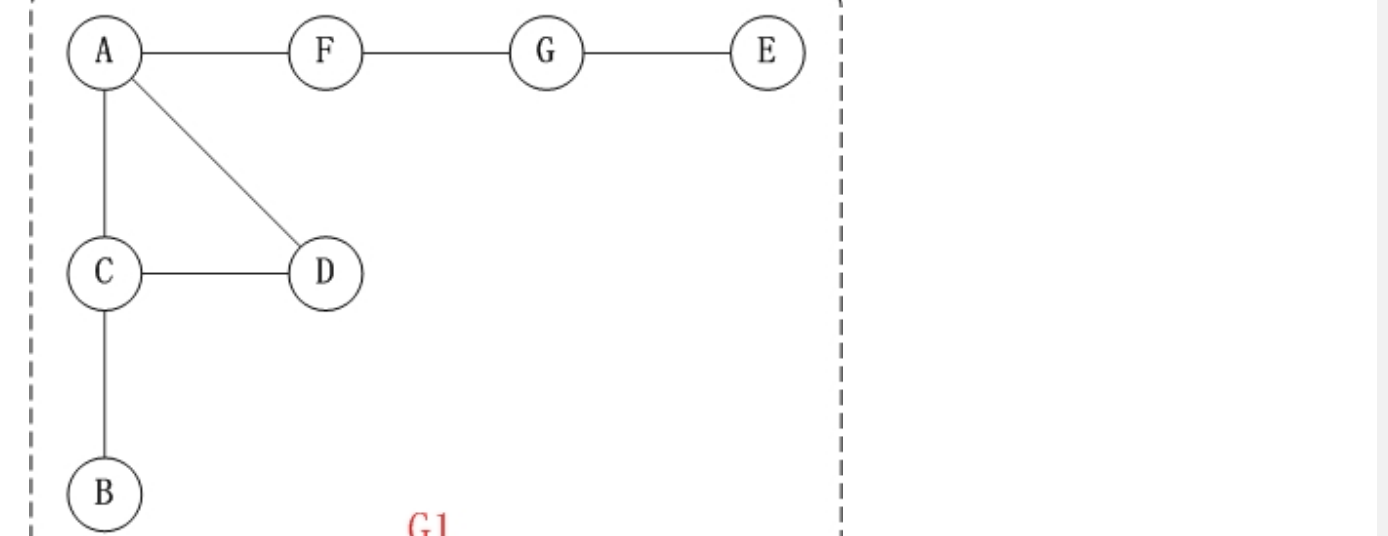
- 就該圖而言,走一遍深度優先遍歷的過程:
- a.以A為起始頂點,進入棧,標記為已訪問的,然後從棧中取出,放進列表中
- b.接著訪問鄰接點C,進入棧,然後放進列表,標記為已訪問
- c.接著訪問鄰接點B,進入棧,然後放進列表,標記為已訪問
- d.接著B已經沒有鄰接點了,而之前的C還有,所以訪問鄰接點D,進入棧,然後放進列表,標記為已訪問
- e.D沒有鄰接點了,但是之前的A還有,所以訪問鄰接點F,進入棧,然後放進列表,標記為已訪問
- f.接著訪問鄰接點G,進入棧,然後放進列表,標記為已訪問
- g.最後是鄰接點E,進入棧,然後放進列表,標記為已訪問
- h.遍歷結束
- 就該圖而言,走一遍深度優先遍歷的過程:
- 深度優先遍歷(類似於樹的前序遍歷)
該例子是無向圖而言的,有向圖是很像的
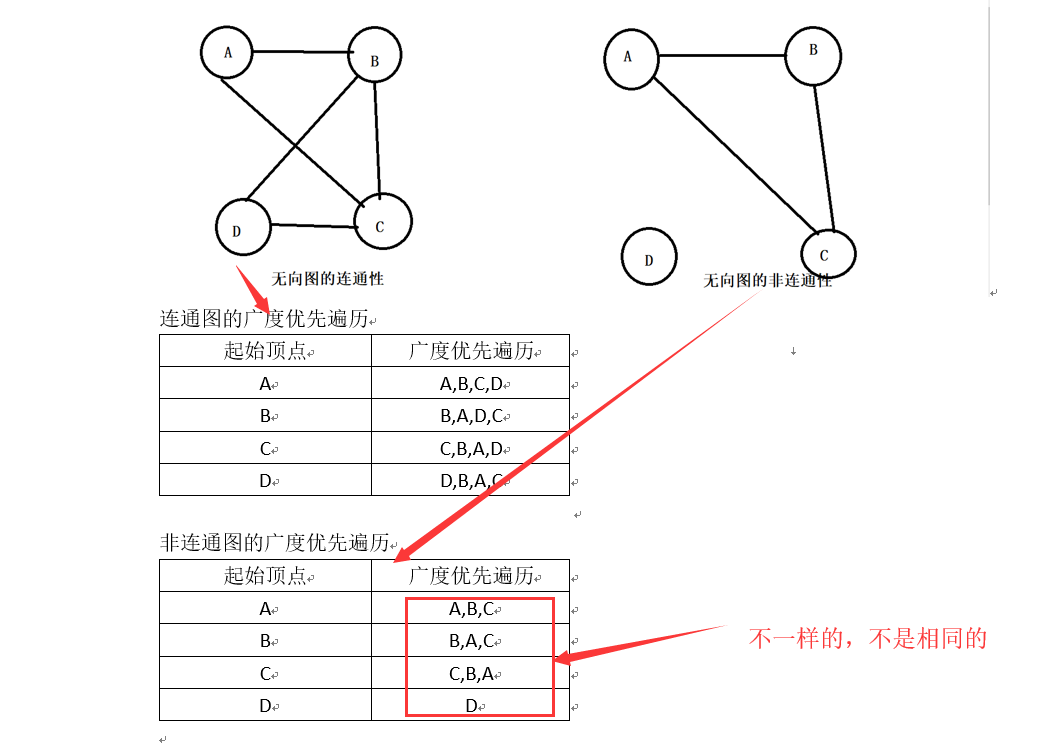
測試連通性:無論哪個為起始頂點,當且僅當廣度優先遍歷中的頂點數目等於圖中的頂點數目時,該圖才是連通的
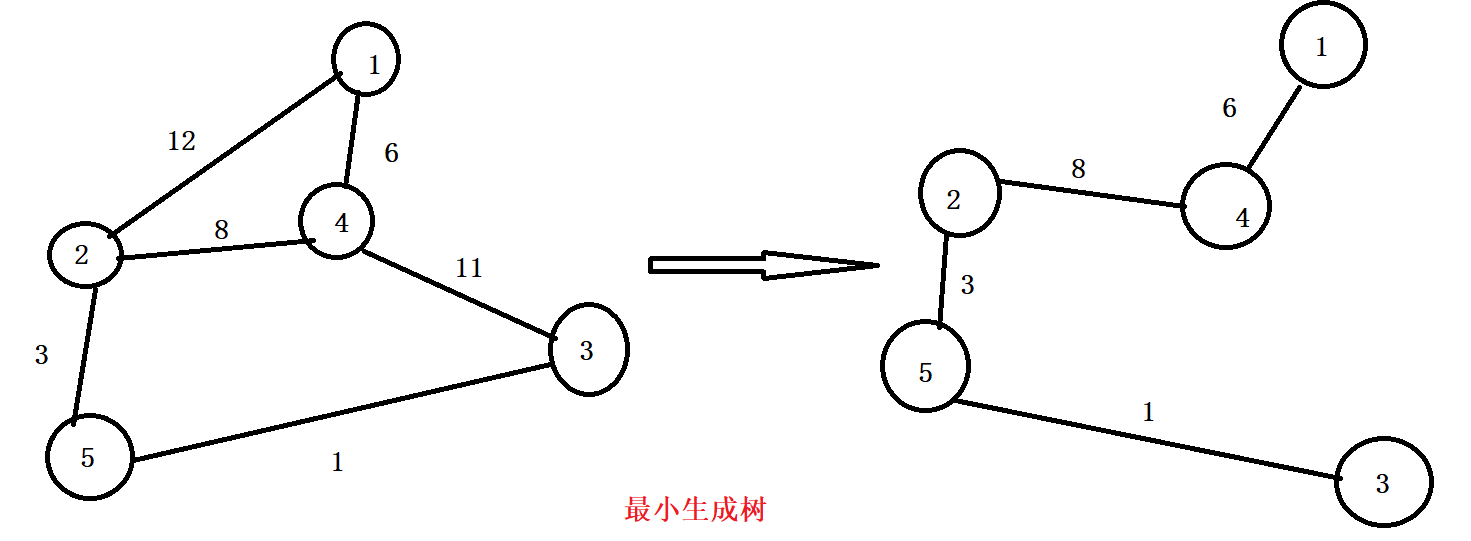
- 最小生成樹
- 生成樹是一棵含有圖中所有頂點和部分變(但可能不是所有邊)的樹
- 最小生成樹其邊的權重總和小於或等於同一圖中其他任何一顆生成樹的權重總和
- 計算最小生成樹一般有兩種演算法:Kruskal和Prim演算法
- 第一種:Prim演算法
- 演算法描述:
- 1.在一個加權連通圖中,頂點集合V。邊集合為E
-
- 隨意選出一個點作為初始頂點,標記為visit,計算全部與之相連線的點的距離,選擇距離最短的,標記visit.
-
- 反覆以下操作,直到全部點都被標記為visit:
- 4.在剩下的點中。計算與已標記visit點距離最小的點,標記visit,證明增加了最小生成樹

- 第二種:Kruskal演算法
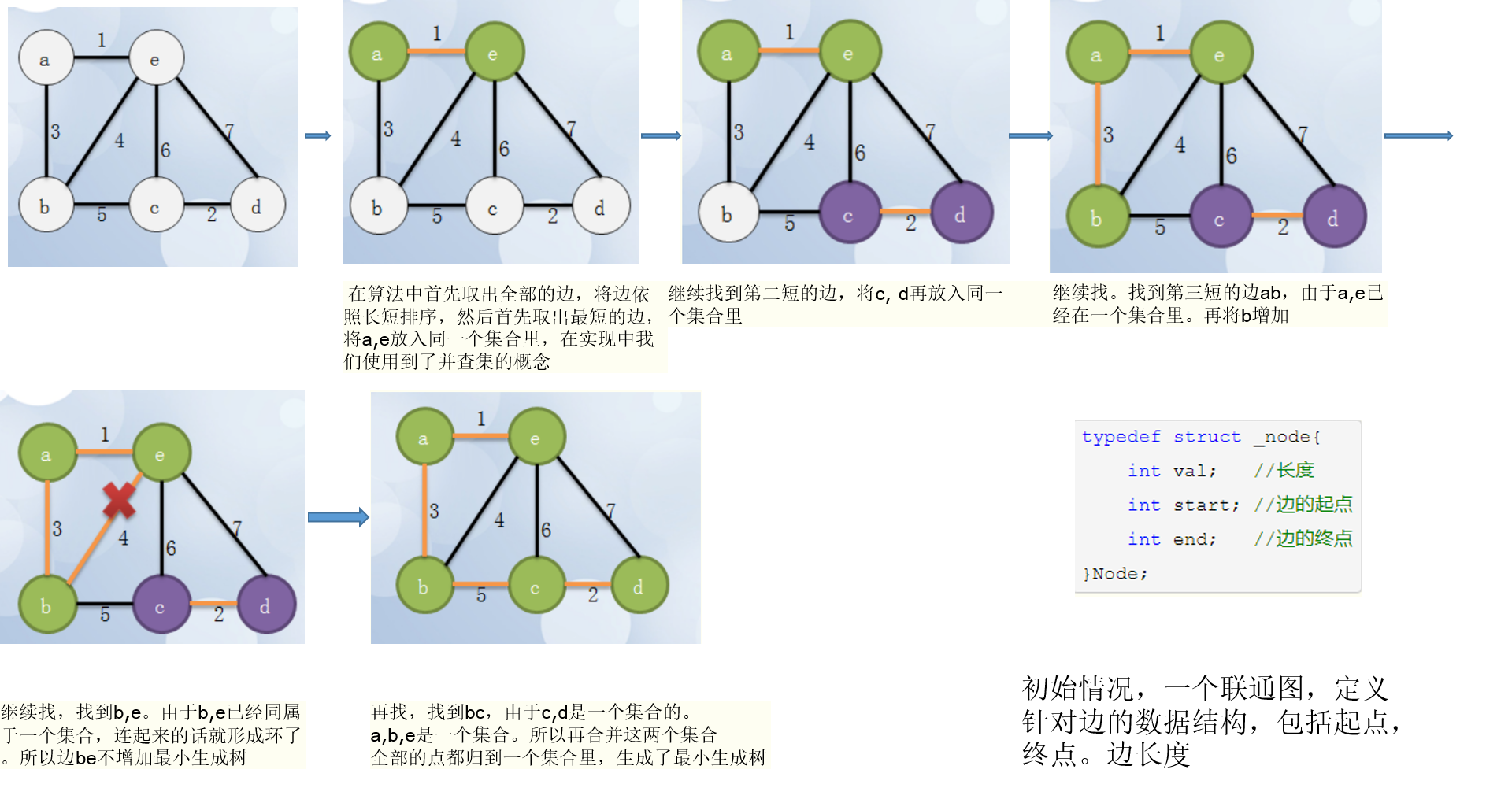
- 判斷最短路徑
- 第一種方法:判定起始頂點與目標頂點之間的字面意義上的最短路徑,也就是兩個頂點間的最小邊數
- 第二種方法:Dijkstra演算法
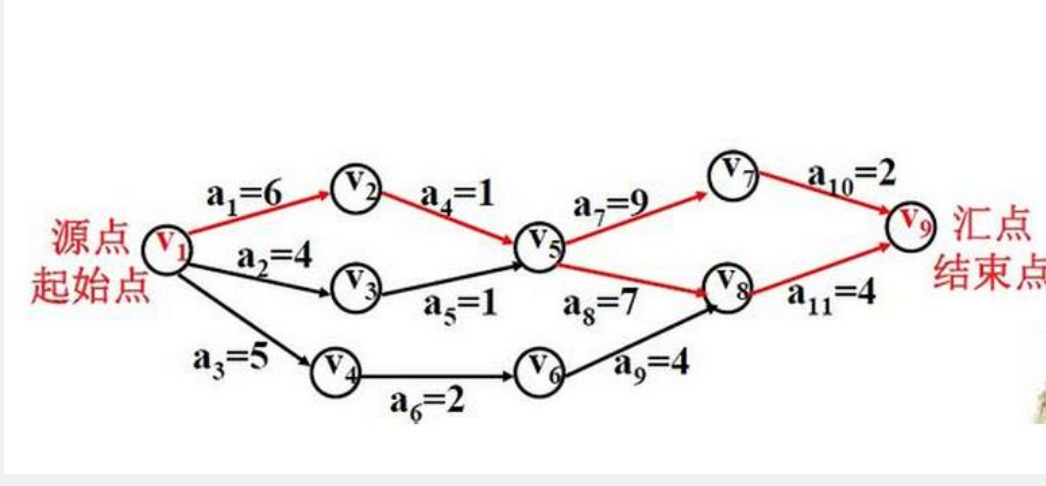
- 基本思路:Dijkstra演算法採用的是一種貪心的策略,宣告一個數組dis來儲存源點到各個頂點的最短距離和一個儲存已經找到了最短路徑的頂點的集合:T,初始時,原點 s 的路徑權重被賦為 0 (dis[s] = 0)。若對於頂點 s 存在能直接到達的邊(s,m),則把dis[m]設為w(s, m),同時把所有其他(s不能直接到達的)頂點的路徑長度設為無窮大。初始時,集合T只有頂點s。 然後,從dis陣列選擇最小值,則該值就是源點s到該值對應的頂點的最短路徑,並且把該點加入到T中,OK,此時完成一個頂點, 然後,我們需要看看新加入的頂點是否可以到達其他頂點並且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短,如果是,那麼就替換這些頂點在dis中的值。 然後,又從dis中找出最小值,重複上述動作,直到T中包含了圖的所有頂點。
例子:

- 過程:
- 我們先宣告一個dis陣列,該陣列初始化的值為:

(1)我們的頂點集T的初始化為:T={v1}。既然是求 v1頂點到其餘各個頂點的最短路程,那就先找一個離V1最近的頂點。通過陣列 dis 可知當前離v1頂點最近是 v3頂點。當選擇了V2頂點後,dis[2](下標從0開始)的值就已經從“估計值”變為了“確定值”,即 v1頂點到 v3頂點的最短路程就是當前 dis[2]值。將V3加入到T中。因為目前離 v1頂點最近的是 v3頂點,並且這個圖所有的邊都是正數,那麼肯定不可能通過第三個頂點中轉,使得 v1頂點到 v3頂點的路程進一步縮短了。因為 v1頂點到其它頂點的路程肯定沒有 v1到 v3頂點短。
既然確定了一個頂點的最短路徑,下面我們就要根據這個新入的頂點V3會有出度,發現以v3 為弧尾的有: < v3,v4 >,那麼我們看看路徑:v1–v3–v4的長度是否比v1–v4短,其實這個已經是很明顯的了,因為dis[3]代表的就是v1–v4的長度為無窮大,而v1–v3–v4的長度為:10+50=60,所以更新dis[3]的值,得到如下結果:
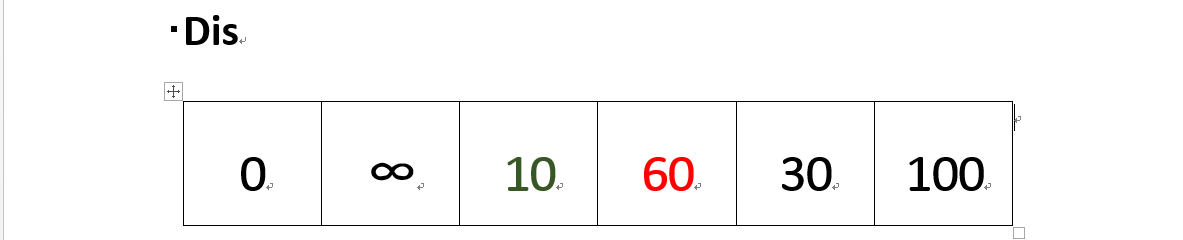
(2)dis[3]要更新為 60。即 v1頂點到 v4頂點的路程即 dis[3]。然後,我們又從除dis[2]和dis[0]外的其他值中尋找最小值,發現dis[4]的值最小,通過之前的內容,可以知道v1到v5的最短距離就是dis[4]的值,然後,我們把v5加入到集合T中,然後,考慮v5的出度是否會影響我們的陣列dis的值,v5有兩條出度:< v5,v4>和 < v5,v6>,然後我們發現:v1–v5–v4的長度為:50,而dis[3]的值為60,所以我們要更新dis[3]的值.另外,v1-v5-v6的長度為:90,而dis[5]為100,所以我們需要更新dis[5]的值。更新後的dis陣列如下圖:

(3)然後,繼續從dis中選擇未確定的頂點的值中選擇一個最小的值,發現dis[3]的值是最小的,所以把v4加入到集合T中,此時集合T={v1,v3,v5,v4},然後,考慮v4的出度是否會影響我們的陣列dis的值,v4有一條出度:< v4,v6>,然後我們發現:v1–v5–v4–v6的長度為:60,而dis[5]的值為90,所以我們要更新dis[5]的值,更新後的dis陣列如下圖:

(4)然後,我們使用同樣原理,分別確定了v6和v2的最短路徑,最後dis的陣列的值如下:

- 圖的實現策略
- 圖的方法和樹中的很類似。會有size、isEmpty、toString、find、最短路徑的操作、判定兩頂點間是否鄰接的操作、構造最小生成樹的操作、測試連通性的操作、兩種遍歷方法的操作
- 對圖結點來說,由於每個結點可以有多達n-1條邊與其他結點相連,因此最好用一種類似於連結串列的動態結點來儲存每個結點帶有的邊,這種連結串列稱為鄰接列表
- 鄰接矩陣:一種二維陣列,其中每個單元都表示了圖中兩個頂點的交接情況,對於無向圖,陣列中的每個單元是一個布林值,對於加權圖,在陣列中還儲存了權重
- 對於無向圖來說,它是雙方向的,所以我們在做鄰接矩陣的時候,其實只需要矩陣對角線的一側即可
- 對於有向圖來說,就和無向圖不同,就根據箭頭之間的鄰接來確定布林值。

教材學習中的問題和解決過程
- 問題1:在看到有向圖時,書中有一個叫拓撲序,我沒有看懂它對它的描寫,不知道什麼意思
問題1解決方案:我上網找了有關的知識,發現拓撲排序是指由某個集合上的一個偏序得到該集合上的一個全序的操作。拓撲排序常用來確定一個依賴關係集中,事物發生的順序。拓撲排序是對有向無環圖的頂點的一種排序,它使得如果存在一條從頂點A到頂點B的路徑,那麼在排序中B出現在A的後面。
- 問題2:我在看程式碼的時候有一處我有點看不懂,在廣序優先遍歷和深度優先遍歷的開頭都有這幾行程式碼,我不懂,為什麼就返回迭代的了呢?
if (!indexIsValid(startIndex)) {
return rls.iterator();
}問題2解決方案:後來在後續的看書中發現,indexIsValid是一個方法,用來判斷這個起始頂點startIndex是否有效,如果有效,才會進行下面的操作,如果無效,其實就是返回空,所以其實return可以為null,但是由於我們是要用迭代器進行輸出的,所以我們返回的是迭代器而不是null。
- 問題3:最開始看書的時候,我對於最小生成樹的那段演算法,因為全是文字描寫,我不懂
問題3解決方案:我在馬原課下課問了譚鑫,他簡單的給我講了一下,後來我又上網看了看具體的畫圖的過程,懂得了,具體總結在課本總結中了。還有,我覺得這種東西,畫圖來表示過程比較容易懂。
程式碼除錯中的問題和解決過程
- 問題1:
- 問題1解決方案:
- 問題2:
- 問題2解決方案:
程式碼託管
(statistics.sh指令碼的執行結果截圖)
上週考試錯題總結
- 翻譯:因為堆是二進位制搜尋樹,所以只有一個正確的位置來插入一個新節點,如果h級是滿的,則是左側h級的下一個開啟位置,或者是左側h+1層的第一個位置。
- 正確:原因其實是堆是具有完整性的
結對及互評
結對
- 部落格中值得學習的或問題:
- 我覺得他的問題提的很好,而且最近的部落格中,都可以看出他有認真的找問題的答案
- 程式碼中值得學習的或問題:
- 他的程式碼我們一起學習的,我覺得他還是要繼續提升的,和我一起!
點評過的同學部落格和程式碼
- 本週結對學習情況
- 20172325
- 結對學習內容
- 一起學習了第十五章的內容
- 一起琢磨書中程式碼的含義
- 一起編寫課後的作業
其他(感悟、思考等,可選)
這一章我看了書,是我們學習的最後一章了,這一章是老師說了很久的圖,我覺得其實和樹有很大的聯絡,而且這章我雖然在做課後作業時還是有很多困難,不知道怎麼做或者不知道下步該做些什麼,但是這一章書中的程式碼我大部分都瞭解了,還是很開心滴。希望在接下來的結對程式設計中,自己能夠努力和別人學習,自己不拖後腿,加油!!!學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 0/0 | 1/1 | 6/6 | |
| 第二週 | 985/985 | 1/1 | 18/24 | |
| 第三週 | 663/1648 | 1/1 | 16/40 | |
| 第四周 | 1742 /3390 | 2/2 | 44/84 | |
| 第五週 | 933/4323 | 1/1 | 23/107 | |
| 第六週 | 1110/5433 | 2/2 | 44/151 | |
| 第七週 | 1536/6969 | 1/1 | 56/207 | |
| 第八週 | 1403/8372 | 2/2 | 60/267 | |
| 第九周 | / | 1/1 | 50/317 |
