本人現在大三，由於準備明天研究生考試，故重新學習複習《訊號與系統》，
再接下來會將自己的一些學習經歷、知識總結與大家分享。對於有所紕漏的地方
希望大家能幫助指出以一同進步。

對於第一章，顯然其重中之重便是系統的六大基本性質，那麼接下來我會以官方解釋及自身的理解加上例題、易錯題、及後面學習知識等一同來闡述並判定這幾個性質（以連續訊號為例、離散訊號類似，有所不同則會一同介紹）：
一、無記憶性
①官方解釋：如果一個系統的輸出僅僅取決於該時刻（即當前時刻）的輸入，那麼就稱這個系統具有無記憶性。
②自身理解：顯然輸出y（t）僅僅取決於輸入x（t），即y（t）=Ax（at）+B 注：A可以是任何除y（t）、x（t）的數值甚至關於t的函式，a只能是常數。即y（t）不能取決於該時刻以前的輸入（若y（t）=x（t-4）則是記憶的），當然也不能取決於該時刻以後的輸入（若y（t）=x（t+4）則既非記憶的也不是非記憶的，在後面可以說它是非因果的）。
③判定方法：
1、利用定義判定：若輸出只取決於當前時刻的輸入，則系統具有無記憶性，即滿足y（t）=Ax（at），A可以為常數也可以為關於t的函式，而a只能為常數。所以說當你做題時或者其他時看到滿足這樣的關係果斷判定！
2、利用衝激響應h（t），對於衝激響應這裡簡單說一下，它其實就是輸入為衝激訊號δ(t)的系統輸出，反正先記著它就是可以描述整個系統的函式就對了（後續再詳細解釋）：當t≠0，h（t）=0，也就是說當h（t）=Kδ(t)時即為無記憶性。對於解釋，你可以想象一下，對於一個系統我對其輸入x（t）=δ(t)，而δ(t)只在t=0出有值為1（可以這樣認為），那麼當系統具有無記憶性的話，輸出y（t）也就是h（t）的值只取決於當前時刻的輸入，而輸入只在t=0出有值，所以h（t）也只能在t=0處有值（因為在其它t處輸入為0，輸出肯定為0）。
④例子
如y（t）=x（t±t0）、x（t^n0）、f(t)x（t）、積分、微分等等都不是無記憶性的；
二、可逆性

①如果一個系統在不同輸入下，導致不同輸出，那麼該系統就是可逆的，在強調一遍是不同輸入（輸入一定要不同）導致不同輸出。
②自身理解：其實類似於高等數學中的單調函式，輸入為x（t），輸出為y（t）（PS：一定要把x（t）看成一個整體，不同是指這個輸入訊號不同），只有當他們滿足單調性時，才具有可逆性。當然此處對於連續訊號與離散訊號略有不同，下面會通過例題介紹。
③判定方法：
1、利用定義判定：對系統加入不同輸入訊號時看輸出有無相同的，當發現其有所差異時，採取特例法（找出不同輸入，這裡的不同輸入就是不同t下的輸入x（t），得到相同輸出這種情況，常令x（t）=δ(t)，或x[n]=δ[n]），即可知其非可逆的。
2、利用衝激響應h（t）可判斷兩個系統是否互為可逆系統：當滿足

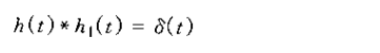
即可知二者互為逆系統。這主要用來判斷兩個系統是否互為可逆系統，其實在頻域表示就為H（jw）x H1（jw）=1。
④例子：
連續：
y（t）=x（t-t0），顯然是可逆的，你看當時x1（t-t0）、x2（t-t0）不同輸入時，則對應的y（t）就不同；
y（t）=sin（x（t-t0）），而這個看起來怪怪的，那麼我們知道sin是個周期函式，那麼顯然的不同x（t=t0）、x（t-t0）+2π不同輸入時就會取到同一個輸出，故不可逆；
對於積分，顯然其也是單調的也就是可逆的；
對於微分，由於那什麼牛頓萊布尼茲公式，我們知道不同的函式即輸入（相差一個常數）微分後有一樣的值即輸出，故不可逆；
y（t）=x（at），a是常數，當x1（at）、x2（at）輸入不同則必然導致y（t）不同，故可逆。
y（t）=tx（at），當x1（t）=δ(t)，x2（t）=2δ(t)不同輸入有相同輸出，則不可逆；
y（t）=x（t）X x（t） ，當x1（t）=δ(t)，x2（t）=-δ(t)不同輸入有相同輸出，則不可逆；
差不多連續時間的就這麼多了，核心還是給t不同從而輸入x（t）不同，看是否會導致y（t）不同。那麼我覺得重中之重還是對離散時間訊號的判斷，你會發現在連續訊號中可逆的在離散訊號中就不可行了；
離散：
y[n]=x[n-n0]，這顯然還是和連續時間一樣的，也是可逆；
**y[n]=x[an]，那個這個是否也一樣呢，**答案是否定的，給個常數a太空泛了，我們就具體一點y[n]=x[2n]，你看這是什麼，這就是壓縮，也就是有一般的訊號會丟失，那麼顯然我只要保留的那部分訊號相同而丟失的訊號不同即有不同輸入就會導致同一輸出，所以呢，這是不可逆的，那麼如果我限定n=奇數說輸出為0，那麼這就是可逆的啦；
y[n]=nx[n]，當輸入為x1[n]=δ(n)、x2[n]=2δ(n)不同輸入時有相同輸出則不可逆；
y[n]=x[n-1]x[n]，當輸入為x1[n]=δ(n)、x2[n]=δ(n-1)不同輸入時有相同輸出則不可逆；
總之，可逆性的判定大概就是這些，核心就是先觀察感覺它不對就找出多對一這樣的關係，也要特別區分離散時間與連續時間的不同，當然也要多利用輸入為δ(n)這種特例。
三、因果性
①官方解釋：如果一個系統的輸出只取決於該時刻（即當前時刻）及過去時刻的輸入，那麼就稱這個系統具有因果性。
②自身理解：有沒發現和無記憶性很像，只是它包括了過去的時刻，其實它講的就是，輸出不能超前於輸入，也就是說不能由還沒發生的輸入就產生了輸出。
③判定方法：
1、利用定義判定：假設當t<t0時，輸入x（t）=0，那麼若輸出在t<t0時y（t）=0，則是因果的，反之則是非因果，聯想到定義很容易理解。
2、利用衝激響應h（t）：當t<0，h（t）=0，則具有因果性，具體解釋見
https://blog.csdn.net/qq_37335890/article/details/83653338
3、利用後續知識拉氏變換，若其為右邊訊號則為因果的，即ROC：|s|>s0；Z變換類似。
④例子
y（t）=x（t-t0），t0>0，顯然輸出和過去的輸入有關，故因果的；
y（t）=x（t+t0），t0>0，顯然輸出和將來的輸入有關，故非因果的，不好理解的話可以帶入假設t0=1，t=2.則輸入為x（2），而輸出為x（3），顯然輸入都還沒發生就發生了輸出；
y（t）=cos（3t）x（t），在這裡，乘積因子cos（3t）對系統的因果性判定不產生影響，故只關注輸入訊號x（t），顯然其是因果的；
**y（t）=x（3t）為例，**其是非因果的，同樣用代入法理解，當t=1，輸入為x（1），而輸出為x（3），輸出超前故非因果，其它因子類似，如y（t）=x（0.5t），其是非因果的，同樣用代入法理解，當t=-1，輸入為x（-1），而輸出為x（-0.5），輸出超前故非因果；
一個特例需特別記住，微分器也是因果的，雖然用數學上的微分性有所違背，但還是將其看作因果的；
總之，因果性是系統最重要的性質之一，因為只有因果的系統物理才可實現，這在後面的學習中會慢慢體會到。
四、穩定性
①官方解釋：如果一個系統的輸入是有界的（即輸入的幅度不是無界增長的），並且輸出也有界，則該系統具有穩定性。
②自身理解：就是輸入訊號小於某個值，那麼輸出訊號也是會小於某個值，當然這個值可能比輸入的界值的大、也可小等等等。
③判定方法：
1、利用定義判定：假定輸入有界，x（t）<B，判斷輸出y（t）是否<f（B）其為關於B的線性運算的確切值（有上限的）；
2、利用衝激響應h（t）：當h（t）絕對可積時，則系統具有穩定性，其實就是|h（t）|的無窮積分小於無窮也就是小於某個確切的值。
3、利用後續知識，拉氏變換其收斂域包括jw軸，Z變換其收斂域包括單位圓，則穩定。
④例子
y（t）=x（t），顯然是因果的，假設x（t）<B，那麼y（t）=x（t）<B；
y（t）=tx（t），顯然是非因果的，假設x（t）<B，那麼y（t）=tx（t），其上限為tB，隨著t的增長會趨於無窮大。
而積分微分也同樣會可能使輸出無界。
所以說當輸入x（t）X f（t）時或對其積分微分時可能會導致其無界，非因果。
五、時不變性
①官方解釋：若系統的特性和行為不隨時間而變，該系統就是時不變的。
②自身理解：其實我覺得這樣理解更好，就是輸入x（t）時移t0，輸出也相應時移t0，即y（t-t0）=F[x（t-t0）]；不過我們今後接觸的基本都是時不變的，所以現在判定只是用來加深理解的；
③判定方法：
1、利用定義判定：看是否滿足y（t-t0）=F[x（t-t0）]；
④例子
還是用例子來理解比較好，先講講具體判斷步驟：
首先是令x1（t）則輸出為y1（t）
再令x2（t）=x1（t-t0）則輸出為y2（t）
再將y1（t-t0）求出與y2(t)相比看是否相等。
對於y（t）=x（at） a為非1常數時，即為時變的；
對於y（t）=f（t）X x（t），f（t）為關於t的函式時，也為時變的；
而對於y（t）=x（t-t0）注意t的係數為1時，系統才為時不變性。
關於這些原因如果有所疑問的話，我後續會總結相關的理解與解釋。
六、線性
①官方解釋：若系統同時滿足比例性（齊次性）和可加性或總稱為疊加性則稱系統具有線性。
②自身理解：這裡有些人覺得分開成比例性和可加性理解更好，也有的人直接就利用疊加性理解，在這裡我們還是用前者來理解，其實都大同小異，都是一樣的思想。
首先我們先明確一下：輸入x1（t）的輸出為y1（t），輸入x2（t）的輸出為y2（t）
比例性：如果滿足輸入ax1（t）的輸出為ay1（t），a為常數，則說明其具有比例性，也就是說輸入變化多少倍輸出也變化多少倍；
可加性：如果滿足輸入x1（t）+x2（t）的輸出為y1（t）+y2（t），則說明其具有可加性，也就是說不同輸入相加的輸出其實就是各個輸入的輸出的代數和；同時滿足比例性與可加性才具有線性。
還是講一講疊加性：其實就是上述二者之和，如果ax1（t）+bx2（t）的輸出為ay1（t）+by2（t），那麼就具有疊加性。滿足疊加性就具有線性
③判定方法：
1、利用定義判定：具體步驟
先考慮輸入x1（t）》》y1（t）
輸入x2（t）》》y2（t）；
再令x3（t）=ax1（t）+bx2（t）；
根據x3（t）求出y3（t）；
看y3（t）是否等於ay1（t）+by2（t）；等於則具有線性。
④例子
還是總結下哪些型別：
y（t）=f（t）X x（at-t0）此類都是線性的，如y（t）=tx（t）；
而對於y（t）=（x（t））^2，次方類的，顯然不滿足比例性，故不是線性的；
總之今後我們遇到的大部分都是線性系統，而對於判斷，一般帶有次方的就不是線性系統。
最後做個總結，其實這些只是為了幫助理解系統的各種性質，至於一些型別的總結也是方便更好理解，當然可能也有一些不足，在這裡說聲抱歉！