機器學習演算法與Python實踐之邏輯迴歸(Logistic Regression)(二)
阿新 • • 發佈:2018-12-10
#!/usr/bin/python # -*- coding:utf-8 -*- import numpy as np from numpy import * import matplotlib.pyplot as plt #處理資料函式 def loadDataSet(): dataMat=[] labelMat=[] fr=open('C:\\Users\\root\\Desktop\\2017machinelearning\\machinelearninginaction-master\\machinelearninginaction-master\\Ch05\\testSet.txt') for line in fr.readlines(): lineArr=line.strip().split() dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat,labelMat def Sigmoid(x): f=1.0/(1+exp(-x)) return f #梯度函式 def gradAscent(dataMat,labelMat): datamatri=mat(dataMat) labelMatri=mat(labelMat).transpose() #轉化為列向量 m,n=shape(datamatri) alpha=0.001 maxCycles=500 weights=ones((n,1)) #迴圈迭代次數maxCycles for i in range(maxCycles): # print i h=Sigmoid(datamatri*weights) #矩陣相乘 初始值 error=(labelMatri-h) #錯誤數\ weights=weights+alpha*datamatri.transpose()*error return weights #隨機梯度函式 def stocgradAscent0(dataMat,labelMat): # datamatri=mat(dataMat) # labelMatri=mat(labelMat).transpose() #轉化為列向量 m,n=shape(dataMat) alpha=0.01 # maxCycles=500 weights=ones(n) print n # print weights #迴圈迭代次數maxCycles for i in range(m): h=Sigmoid(sum(dataMat[i]*weights)) #矩陣相乘 初始值 error=labelMat[i]-h #錯誤數\ weights=weights+alpha*error*dataMat[i] return weights #改進的隨機梯度函式 def stocGradAscent1(dataMatri,classLabels,numIter=150): m,n=shape(dataMatri) weights=ones(n) for j in range(numIter): dataIndex=range(m) for i in range(m): alpha=4/(1.0+j+i)+0.0001 randIndex=int(random.uniform(0,len(dataIndex))) h=Sigmoid(sum(dataMatri[randIndex]*weights)) error=classLabels[randIndex]-h weights=weights+alpha*error*dataMatri[randIndex] del(dataIndex[randIndex]) return weights #畫圖測試 def plotBestFit(weights): # weights=wei.getA() dataMat,labelMat=loadDataSet() dataArr=array(dataMat) # labelMat=array(labelMat) # print type(labelMat[0][0]) n=shape(dataArr)[0] #取行數 xcord1=[] xcord2 = [] ycord1=[] ycord2 = [] for i in range(n): if int(labelMat[i])==1: xcord1.append(dataArr[i,1]) ycord1.append(dataArr[i,2]) # print int(labelMat[i][0]) == 1 else: # print int ( labelMat[i][0] ) == 1 xcord2.append(dataArr[i,1]) ycord2.append(dataArr[i,2]) # weights = gradAscent(dataMat,labelMat) fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(xcord1,ycord1,c='red') ax.scatter(xcord2,ycord2,c='g') x=arange(-3.0,3.0,0.1) y=(-weights[0]-weights[1]*x)/weights[2] ax.plot(x,y.reshape(-1,1)) plt.show() #梯度函式 a,b=loadDataSet() weights=gradAscent(a,b) plotBestFit(weights) #隨機梯度函式 a,b=loadDataSet() weights=stocgradAscent0(array(a),b) plotBestFit(weights) ##改進的隨機梯度函式 a,b=loadDataSet() weights=stocgradAscent0(array(a),b) plotBestFit(weights) #例項分析從疝氣病病症預測病罵的死亡率 def classficatinon(Inter,weights): a=sum(Inter*weights) if Sigmoid(a)>0.5: b=1 else: b=0 return b def colicTest(): frTrain=open('C:\\Users\\root\\Desktop\\2017machinelearning\\machinelearninginaction-master\\machinelearninginaction-master\\Ch05\\horseColicTraining.txt') frTest=open('C:\\Users\\root\\Desktop\\2017machinelearning\\machinelearninginaction-master\\machinelearninginaction-master\\Ch05\\horseColicTest.txt') trainingSet=[] trainingLabels=[] for line in frTrain.readlines(): currLine=line.strip().split('\t') lineArr=[]#特徵向量 for i in range(21): lineArr.append(float(currLine[i])) trainingSet.append(lineArr) trainingLabels.append(float(currLine[21]))#訓練集標籤 trainWeiht=stocGradAscent1(array(trainingSet),trainingLabels,1)#訓練出迴歸係數 errorCount=0 numTestVec=0.0 for line in frTest.readlines(): numTestVec+=1.0 currLine = line.strip ().split ( '\t' ) lineArr = [] # 特徵向量( for i in range ( 21 ): lineArr.append ( float ( currLine[i] ) ) if int(classficatinon(array(lineArr),trainWeiht))!=int(currLine[21]): errorCount+=1 errorRate=(float(errorCount)/numTestVec) print "錯誤率為 %f" % errorRate return errorRate def multiTest(): numTests=1 errorSum=0.0 for k in range(numTests): errorSum+=colicTest() print "after %d 迭代後平均錯誤率為:%f" %(numTests,errorSum/float(numTests)) # colicTest() multiTest()
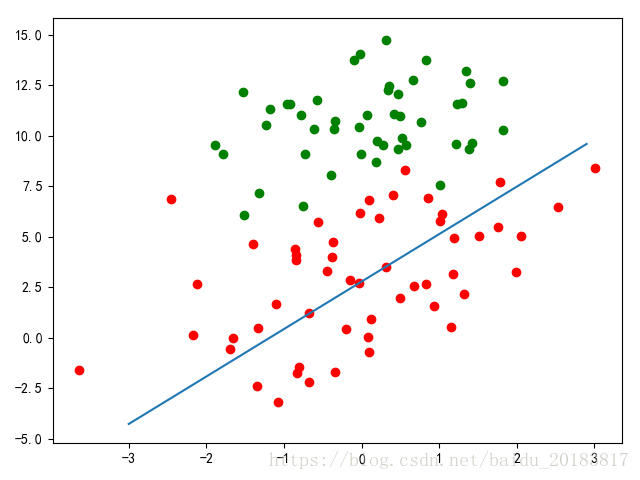
#梯度函式
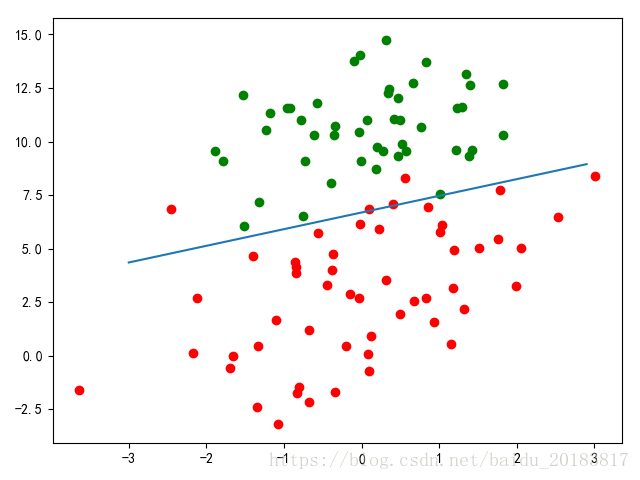
#隨機梯度函式
##改進的隨機梯度函式
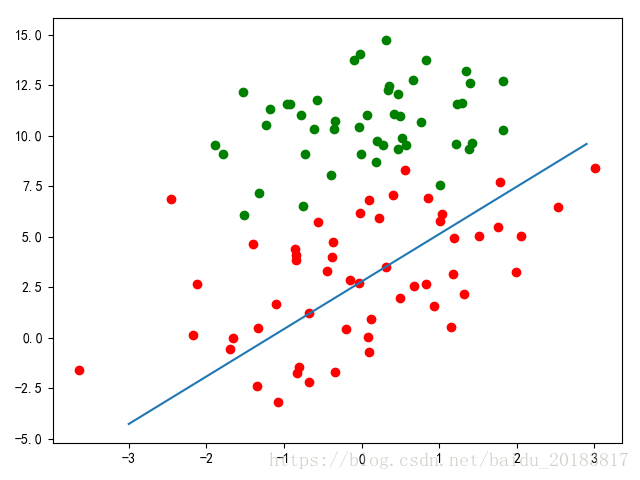
#例項分析從疝氣病病症預測病罵的死亡率
錯誤率為 0.288136
錯誤率為 0.300000
錯誤率為 0.295082
錯誤率為 0.290323
錯誤率為 0.285714
錯誤率為 0.281250
錯誤率為 0.276923
錯誤率為 0.287879
錯誤率為 0.298507
after 10 迭代後平均錯誤率為:0.338806