傳送門：http://codeforces.com/gym/101808/problem/E

E-Floods

You probably heard and even saw the heavy rains that flooded the streets of Damascus recently.

Shahhoud is wondering if he should go to university or not. He asked you to find out how much rainwater is filling his street.

To make things simple, you can imagine Shahhoud's street as a 2D polyline consisting of N

Rain falls from above the polyline down the y axis. Your task is to calculate the total area that keeps rainwater.

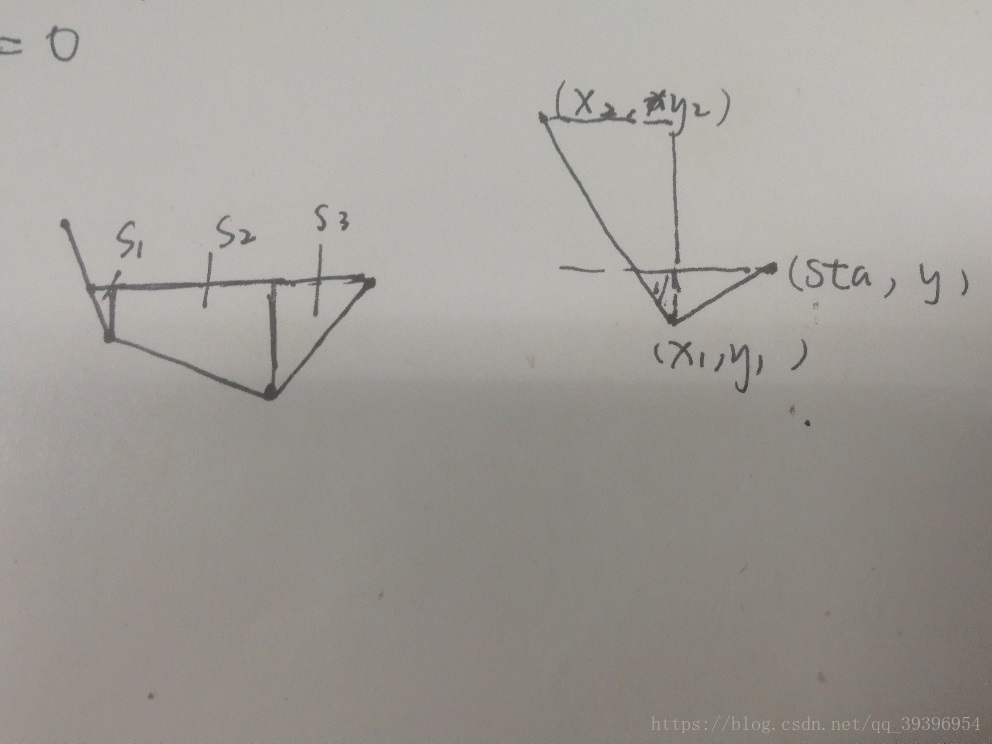
The image below describes the second sample test:

Input

The first line contains a single integer T, the number of test cases.

Each test case starts with a line containing one integer N (1 ≤ N ≤ 105), the number of points in the polyline that represents the street Shahhoud lives in.

The following N lines describe the points of the polyline. The ith line contains two space separated integers xi and yi, the ith point of the polyline. (0 ≤ xi, yi ≤ 106). It is guaranteed that xi < xi + 1 for every 1 ≤ i < N.

Output

For each test case, print one line containing the total area that keeps rainwater.

Your answer will be considered correct if the relative error is less than 10 - 6.

Example

Input

2
2
1 1
2 1
7
1 1
2 0
3 1
5 5
7 2
8 3
9 0

Output

0.00000000
1.83333333

題意：給n個x座標遞增的點，求如圖那樣可以積水的陰影面積。

思路：看左邊的圖，可以考慮把每個水坑分割成三角形或者是梯形。s1的計算方法看右圖，假設當前你在看x2,y2這個點，你發現x1這個點比它低，但是sta那個點限制了高度，陰影面積的計算：豎著的很好算，sta的y去-y1。橫著的取大的三角形x1-x2，再乘以(y-y1)/(y2-y1)。s2和s3計算方法很樸素，就是當前計算的兩個點的x差值，再乘以 限制的sta的y分別減去兩個點的高度再相加(梯形裡就是上底加下底)，最後/2.那麼接下來最後的問題就是怎麼求每次切割的限制高度sta了，分別統計每個點左邊最高點的y和右邊最高點的y，每次取較小的那個，記為sta_y。如果這個點高度比當前讀的點和下一個點都高，那就可以求s3那樣的三角形，或者s2那樣的矩形，如果是在兩個點之間，那就是s1那種相似的計算啦。

程式碼：

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<string>
#include<iostream>
#include<map>
#include<vector>
#include<set>
#include<queue>
using namespace std;
const int maxv=1e5+5;

double ans=0;
int t,n,x[maxv],y[maxv],l[maxv],r[maxv];

int main()
{
	cin>>t;
	while(t--)
	{
		cin>>n;
		for(int i=1;i<=n;i++)
			cin>>x[i]>>y[i];
		int maxx=-1;
		for(int i=1;i<=n;i++)
		{
			maxx=max(maxx,y[i]);
			l[i]=maxx;
		}
		maxx=-1;
		for(int i=n;i>=1;i--)
		{
			maxx=max(maxx,y[i]);
			r[i]=maxx;
		}
		ans=0;
		for(int i=1;i<=n-1;i++)
		{
			int down,up;
			if(y[i]<=y[i+1])
			{
				down=i;
				up=i+1;
			}
			else
			{
				down=i+1;
				up=i;
			}
			int sta=min(l[down],r[down]);
			if(sta>=y[down]&&sta>=y[up])
			{
				ans+=(double)(x[i+1]-x[i])*(double)(2*sta-y[down]-y[up])*0.5;
			}
			else if(sta>y[down])
			{
				ans+=(double)(x[i+1]-x[i])*(double)(sta-y[down])*(double)(sta-y[down])/(y[up]-y[down])*0.5;
			}
		}
		printf("%.8lf\n",ans);

	}
	return 0;
}