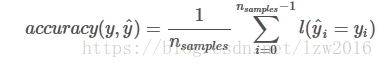sklearn中的模型評估
文章目錄
- 1.介紹
- 2. scoring引數
- 3. 分類metrics
- 3.1 二分類/多分類/多標籤
- 3.2 accuracy_score
- 3.3 Cohen’s kappa
- 3.4 混淆矩陣
- 3.5 分類報告
- 3.7 Jaccard相似度係數score
- 3.8 準確率,召回率與F值
- 3.8.1 二分類
- 3.8.2 多元分類和多標籤分類
- 3.9 ROC
- 4. Multilabel的ranking metrics
- 5.迴歸metrics
- 5.1 可釋方差值(Explained variance score)
- 5.2 平均絕對誤差(Mean absolute error)
- 5.3 均方誤差(Mean squared error)
- 5.4 中值絕對誤差(Median absolute error)
- 5.5 R方值,確定係數
- 6.聚類metrics
- 7. Dummy estimators
1.介紹
有三種不同的方法來評估一個模型的預測質量:
- estimator的score方法:sklearn中的estimator都具有一個score方法,它提供了一個預設的評估法則來解決問題。
- Scoring引數:使用cross-validation的模型評估工具,依賴於內部的scoring策略。見下。
- Metric函式:metrics模組實現了一些函式,用來評估預測誤差。見下。
2. scoring引數
模型選擇和評估工具,例如: grid_search.GridSearchCV 和 cross_validation.cross_val_score,使用scoring引數來控制你的estimator的好壞。
2.1 預定義的值
對於大多數case而說,你可以設計一個使用scoring引數的scorer物件;下面展示了所有可能的值。所有的scorer物件都遵循:高得分,更好效果。如果從mean_absolute_error 和mean_squared_error(它計算了模型與資料間的距離)返回的得分將被忽略。
2.2 從metric函式定義你的scoring策略
sklearn.metric提供了一些函式,用來計算真實值與預測值之間的預測誤差:
- 以_score結尾的函式,返回一個最大值,越高越好
- 以_error結尾的函式,返回一個最小值,越小越好;如果使用make_scorer來建立scorer時,將greater_is_better設為False
接下去會討論多種機器學習當中的metrics。
許多metrics並沒有給出在scoring引數中可配置的字元名,因為有時你可能需要額外的引數,比如:fbeta_score。這種情況下,你需要生成一個合適的scorer物件。最簡單的方法是呼叫make_scorer來生成scoring物件。該函式將metrics轉換成在模型評估中可呼叫的物件。
第一個典型的用例是,將一個庫中已經存在的metrics函式進行包裝,使用定製引數,比如對fbeta_score函式中的beta引數進行設定:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.grid_search import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, scoring=ftwo_scorer)
第二個典型用例是,通過make_scorer構建一個完整的定製scorer函式,該函式可以帶有多個引數:
- 你可以使用python函式:下例中的my_custom_loss_func
- python函式是否返回一個score(greater_is_better=True),還是返回一個loss(greater_is_better=False)。如果為loss,python函式的輸出將被scorer物件忽略,根據交叉驗證的原則,得分越高模型越好。
- 對於分類問題的metrics:如果你提供的python函式是否需要對連續值進行決策判斷,可以將引數設定為(needs_threshold=True)。預設值為False。
- 一些額外的引數:比如f1_score中的bata或labels。
下例使用定製的scorer,使用了greater_is_better引數:
>>> import numpy as np
>>> def my_custom_loss_func(ground_truth, predictions):
... diff = np.abs(ground_truth - predictions).max()
... return np.log(1 + diff)
...
>>> loss = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> score = make_scorer(my_custom_loss_func, greater_is_better=True)
>>> ground_truth = [[1, 1]]
>>> predictions = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(ground_truth, predictions)
>>> loss(clf,ground_truth, predictions)
-0.69...
>>> score(clf,ground_truth, predictions)
0.69...
2.3 實現你自己的scoring物件
你可以生成更靈活的模型scorer,通過從頭構建自己的scoring物件來完成,不需要使用make_scorer工廠函式。對於一個自己實現的scorer來說,它需要遵循兩個原則:
- 必須可以用(estimator, X, y)進行呼叫
- 必須返回一個float的值
3. 分類metrics
sklearn.metrics模組實現了一些loss, score以及一些工具函式來計算分類效能。一些metrics可能需要正例、置信度、或二分決策值的的概率估計。大多數實現允許每個sample提供一個對整體score來說帶權重的分佈,通過sample_weight引數完成。
- 一些二分類(binary classification)使用的case:
matthews_corrcoef(y_true, y_pred) precision_recall_curve(y_true, probas_pred) roc_curve(y_true, y_score[, pos_label, …])
- 一些多分類(multiclass)使用的case:
confusion_matrix(y_true, y_pred[, labels]) hinge_loss(y_true,
pred_decision[, labels, …])
- 一些多標籤(multilabel)的case:
accuracy_score(y_true, y_pred[, normalize, …])
classification_report(y_true, y_pred[, …]) f1_score(y_true, y_pred[,
labels, …]) fbeta_score(y_true, y_pred, beta[, labels, …])
hamming_loss(y_true, y_pred[, classes])
jaccard_similarity_score(y_true, y_pred[, …]) log_loss(y_true,
y_pred[, eps, normalize, …]) precision_recall_fscore_support(y_true,
y_pred) precision_score(y_true, y_pred[, labels, …])
recall_score(y_true, y_pred[, labels, …]) zero_one_loss(y_true,
y_pred[, normalize, …])
- 還有一些可以同時用於二標籤和多標籤(不是多分類)問題:
average_precision_score(y_true, y_score[, …]) roc_auc_score(y_true,
y_score[, average, …])
在以下的部分,我們將討論各個函式。
3.1 二分類/多分類/多標籤
對於二分類來說,必須定義一些matrics(f1_score,roc_auc_score)。在這些case中,預設只評估正例的label,預設的正例label被標為1(可以通過配置pos_label引數來完成)
將一個二分類matrics拓展到多分類或多標籤問題時,我們可以將資料看成多個二分類問題的集合,每個類都是一個二分類。接著,我們可以通過跨多個分類計算每個二分類metrics得分的均值,這在一些情況下很有用。你可以使用average引數來指定。
- macro:計算二分類metrics的均值,為每個類給出相同權重的分值。當小類很重要時會出問題,因為該macro-averging方法是對效能的平均。另一方面,該方法假設所有分類都是一樣重要的,因此macro-averaging方法會對小類的效能影響很大。
- weighted: 對於不均衡數量的類來說,計算二分類metrics的平均,通過在每個類的score上進行加權實現。
- micro: 給出了每個樣本類以及它對整個metrics的貢獻的pair(sample-weight),而非對整個類的metrics求和,它會每個類的metrics上的權重及因子進行求和,來計算整個份額。Micro-averaging方法在多標籤(multilabel)問題中設定,包含多分類,此時,大類將被忽略。
- samples:應用在 multilabel問題上。它不會計算每個類,相反,它會在評估資料中,通過計算真實類和預測類的差異的metrics,來求平均(sample_weight-weighted)
- average:average=None將返回一個數組,它包含了每個類的得分.
多分類(multiclass)資料提供了metric,和二分類類似,是一個label的陣列,而多標籤(multilabel)資料則返回一個索引矩陣,當樣本i具有label j時,元素[i,j]的值為1,否則為0.
3.2 accuracy_score
accuracy_score函式計算了準確率,不管是正確預測的fraction(default),還是count(normalize=False)。
在multilabel分類中,該函式會返回子集的準確率。如果對於一個樣本來說,必須嚴格匹配真實資料集中的label,整個集合的預測標籤返回1.0;否則返回0.0.
預測值與真實值的準確率,在n個樣本下的計算公式如下:
1(x)為指示函式。
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2
在多標籤的case下,二分類label:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
3.3 Cohen’s kappa
函式cohen_kappa_score計算了Cohen’s kappa估計。這意味著需要比較通過不同的人工標註(numan annotators)的標籤,而非分類器中正確的類。
kappa score是一個介於(-1, 1)之間的數. score>0.8意味著好的分類;0或更低意味著不好(實際是隨機標籤)
Kappa score可以用在二分類或多分類問題上,但不適用於多標籤問題,以及超過兩種標註的問題。
3.4 混淆矩陣
confusion_matrix函式通過計算混淆矩陣,用來計算分類準確率。
預設的,在混淆矩陣中的i,j指的是觀察的數目i,預測為j,示例:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
示例:
- Confusion matrix
- Recognizing hand-written digits
- Classification of text documents using sparse features
3.5 分類報告
classification_report函式構建了一個文字報告,用於展示主要的分類metrics。 下例給出了一個小示例,它使用定製的target_names和對應的label:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 2, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 1.00 1.00 2
avg / total 0.67 0.80 0.72 5
示例:
##3 3.6 Hamming loss
hamming_loss計算了在兩個樣本集裡的平均漢明距離或平均Hamming loss。
ˆyj是對應第j個label的預測值,
yj是對應的真實值
nlabels是類目數
那麼兩個樣本間的Hamming loss為LHamming,定義如下:
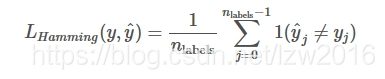
其中:1(x)為指示函式。
>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25
在多標籤(multilabel)的使用二元label指示器的情況:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75
注意:在多分類問題上,Hamming loss與y_true 和 y_pred 間的Hamming距離相關,它與0-1 loss相類似。然而,0-1 loss會對不嚴格與真實資料集相匹配的預測集進行懲罰。因而,Hamming loss,作為0-1 loss的上界,也在0和1之間;預測一個合適的真實label的子集或超集將會給出一個介於0和1之間的Hamming loss.
3.7 Jaccard相似度係數score
jaccard_similarity_score函式會計算兩對label集之間的Jaccard相似度係數的平均(預設)或求和。它也被稱為Jaccard index.
第i個樣本的Jaccard相似度係數(Jaccard similarity coefficient),真實標籤集為yi,預測標籤集為:ˆyj,其定義如下:
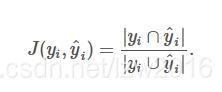
在二分類和多分類問題上,Jaccard相似度係數score與分類的正確率(accuracy)相同:
>>> import numpy as np
>>> from sklearn.metrics import jaccard_similarity_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> jaccard_similarity_score(y_true, y_pred)
0.5
>>> jaccard_similarity_score(y_true, y_pred, normalize=False)
2
在多標籤(multilabel)問題上,使用二元標籤指示器:
>>> jaccard_similarity_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.75
3.8 準確率,召回率與F值
準確率(precision)可以衡量一個樣本為負的標籤被判成正,召回率(recall)用於衡量所有正例。
F-meature(包括:Fβ和F1”),可以認為是precision和recall的加權調和平均(weighted harmonic mean)。一個Fβ值,最佳為1,最差時為0. 如果β=1,那麼Fβ和F1相等,precision和recall的權重相等。
precision_recall_curve會根據預測值和真實值來計算一條precision-recall典線。
average_precision_score則會預測值的平均準確率(AP: average precision)。該分值對應於precision-recall曲線下的面積。
sklearn提供了一些函式來分析precision, recall and F-measures值:
average_precision_score:計算預測值的AP
f1_score: 計算F1值,也被稱為平衡F-score或F-meature
fbeta_score: 計算F-beta score
precision_recall_curve:計算不同概率閥值的precision-recall對
precision_recall_fscore_support:為每個類計算precision, recall, F-measure 和 support
precision_score: 計算precision
recall_score: 計算recall
注意:precision_recall_curve只用於二分類中。而average_precision_score可用於二分類或multilabel指示器格式
3.8.1 二分類
在二元分類中,術語“positive”和“negative”指的是分類器的預測類別(expectation),術語“true”和“false”則指的是預測是否正確(有時也稱為:觀察observation)。給出如下的定義:
實際類目(observation)
預測類目(expectation) TP(true positive)結果:Correct FP(false postive)結果:Unexpected
FN(false negative)結果: Missing TN(true negtive)結果:Correct
在這個上下文中,我們定義了precision, recall和F-measure:

這裡是一個二元分類的示例:
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([ 0.66..., 1. ]), array([ 1. , 0.5]), array([ 0.71..., 0.83...]), array([2, 2]...))
>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([ 0.66..., 0.5 , 1. , 1. ])
>>> recall
array([ 1. , 0.5, 0.5, 0. ])
>>> threshold
array([ 0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.79...
3.8.2 多元分類和多標籤分類
在多分類(Multiclass)和多標籤(multilabel)分類問題上,precision, recall, 和 F-measure的概念可以獨立應用到每個label上。有一些方法可以綜合各標籤上的結果,通過指定average_precision_score (只能用在multilabel上), f1_score, fbeta_score, precision_recall_fscore_support, precision_score 和 recall_score這些函式上的引數average可以做到。
注意:
“micro”選項:表示在多分類中的對所有label進行micro-averaging產生一個平均precision,recall和F值
“weighted”選項:表示會產生一個weighted-averaging的F值。
可以考慮下面的概念:
y是(sample, label)pairs的預測集
ˆy是(sample, label)pairs的真實集
L是labels的集
S是labels的集
ˆy是y的子集,樣本s,比如:y_s := \left{(s’, l) \in y | s’ = s \right}
yl表示label l的y子集
同樣的,ys和yl都是ˆy的子集
P(A,B):=|A∩B||A|
R(A,B):=|A∩B||B| 在處理B=∅時方式更不同;該實現採用R(A,B):=0,且與P相類似。
Fβ(A,B):=(1+β2)P(A,B)×R(A,B)β2P(A,B)+R(A,B)
程式碼:
>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
...
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
...
(array([ 0.66..., 0. , 0. ]), array([ 1., 0., 0.]), array([ 0.71..., 0. , 0. ]), array([2, 2, 2]...))
對於多分類問題,對於一個“negative class”,有可能會排除一些標籤:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0
類似的,在資料集樣本中沒有出現的label不能用在macro-averaging中。
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
...
0.166...
3.9 ROC
roc_curve計算了ROC曲線。Wikipedia如下:
“A receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied. It is created by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate), at various threshold settings. TPR is also known as sensitivity, and FPR is one minus the specificity or true negative rate.”
該函式需要二分類的真實值和預測值,它可以是正例的概率估計,置信值,或二分決策值。下例展示瞭如何使用:
>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. , 0.5, 0.5, 1. ])
>>> tpr
array([ 0.5, 0.5, 1. , 1. ])
>>> thresholds
array([ 0.8 , 0.4 , 0.35, 0.1 ])
roc_auc_score函式計算了ROC曲線下面的面積,它也被稱為AUC或AUROC。通過計算下面的面積,曲線資訊被歸一化到1內。
>>> import numpy as np
>>> from sklearn.metrics import roc_auc_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> roc_auc_score(y_true, y_scores)
0.75
在多標籤(multi-label)分類上,roc_auc_score通過對上面的label進行平均。
對比於其它metrics: accuracy、 Hamming loss、 F1-score, ROC不需要為每個label優化一個閥值。roc_auc_score函式也可以用於多分類(multi-class)問題上。如果預測的輸出已經被二值化。
示例:
Receiver Operating Characteristic (ROC)
Receiver Operating Characteristic (ROC) with cross validation
Species distribution modeling
4. Multilabel的ranking metrics
在多標籤學習上,每個樣本都具有多個真實值label與它對應。它的目的是,為真實值label得到最高分或者最好的rank。
4.1 範圍誤差(Coverage error)
coverage_error計算了那些必須在最終預測(所有真實的label都會被預測)中包含的labels的平均數目。如果你想知道有多少top高分labels(top-scored-labels)時它會很有用,你必須以平均的方式進行預測,不漏過任何一個真實label。該metrics的最優值是對真實label求平均。

其中:$ \text{rank}{ij} = \left|\left{k: \hat{f}{ik} \geq \hat{f}_{ij} \right}\right| $。給定rank定義,通過給出最大的rank,來打破y_scores。
示例如下:
>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5
4.2 Label ranking平均準確率
label_ranking_average_precision_score函式實現了Label ranking平均準確率 :LRAP(label ranking average precision)。該metric與average_precision_score有關聯,但它基於label ranking的概念,而非 precision/recall 。
LRAP會對每個樣本上分配的真實label進行求平均,真實值的比例 vs. 低分值labels的總數。如果你可以為每個樣本相關的label給出更好的rank,該指標將產生更好的分值。得到的score通常都會比0大,最佳值為1。如果每個樣本都只有一個相關聯的label,那麼LRAP就與平均倒數排名:mean reciprocal rank

其中:
$ \mathcal{L}{ij} = \left{k: y{ik} = 1, \hat{f}{ik} \geq \hat{f}{ij} \right} $,
$ \text{rank}{ij} = \left|\left{k: \hat{f}{ik} \geq \hat{f}_{ij} \right}\right| $
|⋅|是l0 正規化或是資料集的基數。
該函式的示例:
>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score)
0.416...
5.迴歸metrics
sklearn.metrics 實現了許多種loss, score,untility函式來測評迴歸的效能。其中有一些可以作了增加用於處理多輸出(multioutput)的情況:
mean_squared_error,
mean_absolute_error
explained_variance_score
r2_score
這些函式具有一個multioutput關鍵引數,它指定了對於每一個單獨的target是否需要對scores/loss進行平均。預設值為’uniform_average’,它會對結果進行均勻加權平均。如果輸出的ndarray的shape為(n_outputs,),那麼它們返回的entries為權重以及相應的平均權重。如果multioutput引數為’raw_values’,那麼所有的scores/losses都不改變,以raw的方式返回一個shape為(n_outputs,)的陣列。
r2_score和explained_variance_score 對於multioutput引數還接受另一個額外的值:’variance_weighted’。該選項將通過相應target變數的variance產生一個為每個單獨的score加權的值。該設定將會對全域性捕獲的未歸一化的variance進行量化。如果target的variance具有不同的規模(scale),那麼該score將會把更多的重要性分配到那些更高的variance變數上。
對於r2_score的預設值為multioutput=’variance_weighted’,向後相容。後續版本會改成uniform_average。
5.1 可釋方差值(Explained variance score)
explained_variance_score解釋了explained variance regression score
如果ˆy是估計的target輸出,y為相應的真實(correct)target輸出,Var為求方差(variance),即標準差的平方,那麼可釋方差(explained variance)的估計如下:

最好的可能值為1.0,越低表示越差。
示例如下:
>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
...
array([ 0.967..., 1. ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.990...
5.2 平均絕對誤差(Mean absolute error)
mean_absolute_error函式將會計算平均絕對誤差,該指標對應於絕對誤差loss(absolute error loss)或l1正規化loss(l1-norm loss)的期望值。
示例:
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([ 0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.849...
5.3 均方誤差(Mean squared error)
mean_squared_error用於計算平均平方誤差,該指標對應於平方(二次方)誤差loss(squared (quadratic) error loss)的期望值。
示例為:
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083...
示例:
5.4 中值絕對誤差(Median absolute error)
median_absolute_error是很令人感興趣的,它對異類(outliers)的情況是健壯的。該loss函式通過計算target和prediction間的絕對值,然後取中值得到。
MedAE的定義如下:
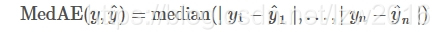
median_absolute_error不支援multioutput。
示例:
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
5.5 R方值,確定係數
r2_score函式用於計算R²(確定係數:coefficient of determination)。它用來度量未來的樣本是否可能通過模型被很好地預測。分值為1表示最好,它可以是負數(因為模型可以很糟糕)。一個恆定的模型總是能預測y的期望值,忽略掉輸入的feature,得到一個R^2為0的分值。
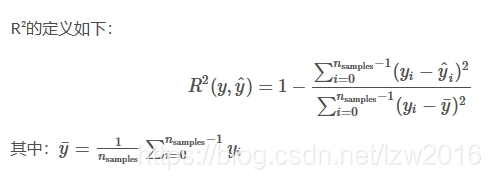
示例:
>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
...
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
...
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
...
array([ 0.965..., 0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.925...
示例:
6.聚類metrics
sklearn.metrics也提供了聚類的metrics。更多細節詳見:
7. Dummy estimators
當進行監督學習時,一個簡單明智的check包括:使用不同的規則比較一個estimator。DummyClassifier實現了三種簡單的策略用於分類:
stratified:根據訓練集的分佈來生成隨機預測
most_frequent:在訓練集中總是預測最頻繁的label
prior:總是預測分類最大化分類優先權(比如:most_frequent),predict_proba返回分類優化權
uniform:以均勻方式隨機生成預測
constant:由使用者指定,總是預測一個常量的label。該方法的一個最主要動機是:F1-scoring,其中正例是最主要的。
注意,所有的這些策略中,predict方法會完成忽略輸入資料!
示例,我們首先建立一個imbalanced的資料集:
>>> from sklearn.datasets import load_iris
>>> from sklearn.cross_validation import train_test_split
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
下一步,比較下SVC的accuary和most_frequent:
>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.63...
>>> clf = DummyClassifier(strategy='most_frequent',random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(constant=None, random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)
0.57...
我們可以看到SVC並不比DummyClassifier好很多,接著,我們換下kernel:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.97...
我們可以看到,accuracy增強到了幾乎100%。如果CPU開銷不大,這裡建議再做下cross-validation。如果你希望在引數空間進行優化,我們強烈推薦你使用GridSearchCV。
更一般的,分類器的accuracy太接近於隨機,這可能意味著有可能會出問題:features沒有用,超引數沒有被正確設定,分類器所用的資料集imbalance,等等。。。
DummyRegressor也實現了4種簡單的方法:
mean:通常預測訓練target的均值。
median:通常預測訓練target的中值。
quantile:預測由使用者提供的訓練target的分位數
constant:常量
在上面的所有策略,predict完全忽略輸入資料。
參考:
http://scikit-learn.org/stable/modules/model_evaluation.html