假如我們有一個帶標籤的資料集D，我們如何選擇最優的模型？ 衡量模型好壞的標準是看這個模型在新的資料集上面表現的如何，也就是看它的泛化誤差。因為實際的資料沒有標籤，所以泛化誤差是不可能直接得到的。於是我們需要在資料集D上面劃分出來一小部分資料測試D的效能，用它來近似代替泛化誤差。

留出法

留出法的想法很簡單，將原始資料直接劃分為互斥的兩類，其中一部分用來訓練模型，另外一部分用來測試。前者就是訓練集，後者就是測試集。通常訓練集和測試集的比例為7:3。

需要注意：訓練\測試集的劃分要儘可能保持資料分佈的一致性，避免因資料劃分過程引入額外的偏差而對最終結果產生影響。那麼問題來啦

要注意，train_test_split沒有采用分層取樣，相當於對資料集進行了shuffle後按照給定的test_size進行資料集劃分。

from sklearn import datasets  #資料集模組
from sklearn.model_selection import train_test_split  #訓練集和測試集分割模組
from sklearn.neighbors import KNeighborsClassifier

iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
train_x,test_x,train_y,test_y = train_test_split(iris_x,iris_y,test_size=0.3)
KNN = KNeighborsClassifier(n_neighbors=5)
KNN.fit(train_x,train_y)
print(KNN.score(test_x,test_y))
 

0.9555555555555556

留出法非常的簡單。但是存在一些問題，比如有些模型還需要進行超引數評估，這個時候還需要劃分一類資料集，叫做驗證集。最後資料集的劃分劃分變成了這樣：訓練集，驗證集還有測試集。 訓練集是為了進行模型的訓練，驗證集是為了進行引數的調整，測試集是為了看這個模型的好壞。

但是，上面的劃分依然有問題，劃分出來驗證集還有測試集，那麼我們的訓練集會變小。並且還有一個問題，那就是我們的模型會隨著我們選擇的訓練集和驗證集不同而不同。所以這個時候，我們引入了交叉驗證。

交叉驗證法資料集切分策略

1、 KFold方法 K折交叉驗證

將資料集分為k等份，對於每一份資料集，其中k-1份用作訓練集，單獨的那一份用作測試集。
sklearn中的方法實現為

from sklearn.model_selection import KFold
kf = KFold(n_splits=2)

2、 RepeatedKFold p次k折交叉驗證

在實際當中，我們只進行一次k折交叉驗證還是不夠的，我們需要進行多次，最典型的是：10次10折交叉驗證，RepeatedKFold方法可以控制交叉驗證的次數。
sklearn中的方法實現為

from sklearn.model_selection import RepeatedKFold
kf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=0)

3、 LeaveOneOut 留一法

留一法是k折交叉驗證當中，k=n（n為資料集個數）的情形
sklearn中的方法實現為

from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()

4、 LeavePOut 留P法

和留一法原理類似，只不過每次測試集抽取的樣本數由1變為P
sklearn中的方法實現為

from sklearn.model_selection import LeavePOut
loo = LeavePOut(p=2)

5、 ShuffleSplit 隨機分配

使用ShuffleSplit方法，可以隨機的把資料打亂，然後分為訓練集和測試集。它還有一個好處是可以通過random_state這個種子來重現我們的分配方式，如果沒有指定，那麼每次都是隨機的。
sklearn中的方法實現為

from sklearn.model_selection import ShuffleSplit
ss = ShuffleSplit(n_splits=4, random_state=0, test_size=0.25)

6、 StratifiedKFold 分層k折交叉驗證

StratifiedKFold用法類似Kfold，但是他是分層取樣，確保訓練集，測試集中各類別樣本的比例與原始資料集中相同。

sklearn中的方法實現為

from sklearn.model_selection import StratifiedKFold
sk = StratifiedKFold(n_splits=4, random_state=0)

哈哈哈，重點來啦，以下是對上述劃分資料集的個人理解
1、對於KFold，它不會考慮分層取樣，這樣會引入誤差。如下所示：

X = [1,2,3,4,5,6,7,8,9,10,11,12]
y = [1,1,1,0,1,0,1,1,1,0,1,0]
kf = KFold(n_splits=4)
for train_index, test_index in kf.split(X,y):
    print('train_index', train_index, 'test_index', test_index)

train_index [ 3  4  5  6  7  8  9 10 11] test_index [0 1 2]
train_index [ 0  1  2  6  7  8  9 10 11] test_index [3 4 5]
train_index [ 0  1  2  3  4  5  9 10 11] test_index [6 7 8]
train_index [0 1 2 3 4 5 6 7 8] test_index [ 9 10 11]

我們可以看到，它只是依次的選取測試集，剩下的即為訓練集。不會考慮總樣本中各個類別所佔的比例。
如果令shuffle=True，則隨機取樣。
如果令random_state為一個常值，則每次得到的結果都一樣，否則每一次得到的劃分結果都不一樣。

2、如果想考慮分層取樣，那就要採用StratifiedKFold，如下所示

X = [1,2,3,4,5,6,7,8,9,10,11,12]
y = [1,1,1,0,1,0,1,1,1,0,1,0]
sf = StratifiedKFold(n_splits=4)
for train_index, test_index in sf.split(X,y):
    print('train_index', train_index, 'test_index', test_index)

train_index [ 2  4  5  6  7  8  9 10 11] test_index [0 1 3]
train_index [ 0  1  3  6  7  8  9 10 11] test_index [2 4 5]
train_index [ 0  1  2  3  4  5  8 10 11] test_index [6 7 9]
train_index [0 1 2 3 4 5 6 7 9] test_index [ 8 10 11]

從上面可以看出，每一次劃分之後，訓練集和測試集中各個類別的比例都與總樣本中各個類別的比例相同。這樣就可以避免一些誤差。

如果令shuffle=True，則隨機取樣。但不同於KFold，即使隨機取樣，也要符合分層取樣的原則。
如果令random_state為一個常值，則每次得到的結果都一樣，否則每一次得到的劃分結果都不一樣。

3、ShuffleSplit
隨機劃分。它與Kfold的區別是：KFold中的k個測試集必須互斥，而這個裡面不用保證互斥。
同樣，如果random_state為一個常值int，那麼每次分組的結果都一樣。即可以通過random_state這個種子來重現我們的分配方式，如果沒有指定，那麼每次都是隨機的。

X = [1,2,3,4,5,6,7,8,9,10,11,12]
y = [1,1,1,0,1,0,1,1,1,0,1,0]
ss = ShuffleSplit(n_splits=4,test_size=0.25)
for train_index, test_index in ss.split(X,y):
    print('train_index', train_index, 'test_index', test_index)

train_index [ 9 10  7  1  2  5 11  0  6] test_index [8 3 4]
train_index [ 7 10  5  6  8  3  1  9  4] test_index [ 2 11  0]
train_index [ 4 10  1 11  8  3  7  9  6] test_index [5 0 2]
train_index [ 4  2  3  7 11  6  9  8  1] test_index [ 0  5 10]

交叉驗證

上面講的是如何使用交叉驗證進行資料集的劃分。當我們用交叉驗證的方法並且結合一些效能度量方法來評估模型好壞的時候，我們可以直接使用sklearn當中提供的交叉驗證評估方法，這些方法如下：

1、cross_value_score

利用交叉驗證對某個超引數模型進行打分。

from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets  #資料集模組
iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target

knn = KNeighborsClassifier(n_neighbors=5)
print(cross_val_score(knn,iris_x,iris_y,cv=10,scoring='accuracy'))
print(cross_val_score(knn,iris_x,iris_y,cv=10,scoring='accuracy').mean())

[1.         0.93333333 1.         1.         0.86666667 0.93333333
 0.93333333 1.         1.         1.        ]
0.9666666666666668

當cv為int型時，預設使用KFold或StratifiedKFold。預設是以scoring=’f1_macro’進行評測的。所有的打分選項如下：

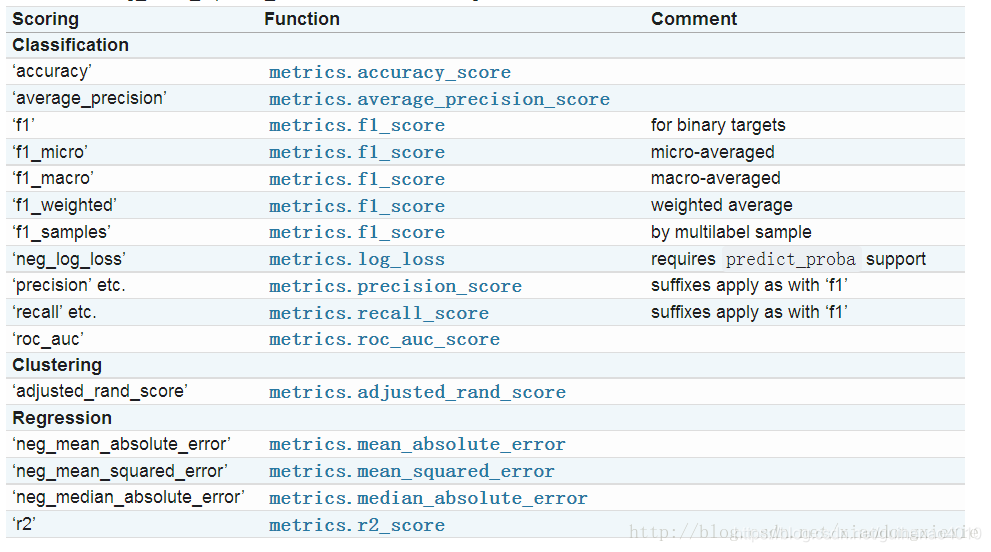
最喜歡的個人理解又來啦_?_
我們知道交叉驗證是為了驗證摸個模型超引數條件下的模型是否訓練的比較好。因此我們可以設定一個迴圈，迴圈變數為超引數的取值，便可以得到一系列交叉驗證的結果。由此便可以得到交叉驗證結果最好的那個超引數。

2、validation_curve

這個就是交叉驗證曲線，跟我們上面設定迴圈變數的方法一致。不得不感嘆sklearn真的很強大啊。

from sklearn import datasets  #資料集模組
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve

iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target

para_range = np.arange(1,30)
train_loss,test_loss = validation_curve(KNeighborsClassifier(),iris_x,iris_y,
                                        param_name='n_neighbors',param_range=para_range,
                                        cv=10,scoring='accuracy')
train_accuracy = np.mean(train_loss,axis=1)
test_accuracy = np.mean(test_loss,axis=1)
plt.plot(train_accuracy,color='r',label='train')
plt.plot(test_accuracy,color='b',label='test')
plt.xlabel('n_neighbors')
plt.ylabel('accuracy')
plt.legend()
plt.show()

其中param_range為超引數的取值範圍，param_name為要改變的超引數的名稱。

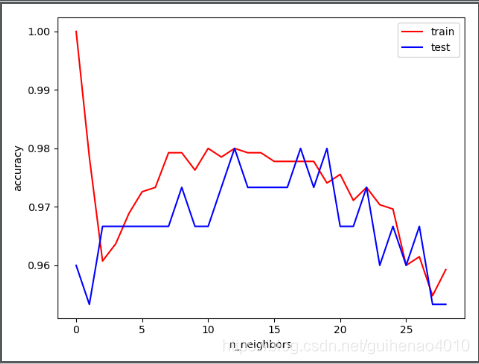
驗證曲線和學習曲線的區別是，橫軸為某個超引數的一系列值，由此來看不同引數設定下模型的準確率，而不是不同訓練集大小下的準確率。

從驗證曲線上可以看到隨著超引數設定的改變，模型可能從欠擬合到合適再到過擬合的過程，進而選擇一個合適的設定，來提高模型的效能。

需要注意的是如果我們使用驗證分數來優化超引數，那麼該驗證分數是有偏差的，它無法再代表模型的泛化能力，我們就需要使用其他測試集來重新評估模型的泛化能力。

3、learning_curve 學習曲線

學習曲線可以判斷我們的模型是處於過擬合還是欠擬合的狀態。

rom sklearn.model_selection import learning_curve
import numpy as np
from sklearn import datasets  #資料集模組
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target

train_sizes, train_loss, test_loss = learning_curve(
    KNeighborsClassifier(n_neighbors=5), iris_x, iris_y, cv=10, scoring='neg_mean_squared_error',
    train_sizes=[0.1, 0.15, 0.25, 0.35,0.45,0.55,0.65,0.75,0.85, 1])
train_loss = -np.mean(train_loss,axis=1)
test_loss = -np.mean(test_loss,axis=1)
plt.plot(train_sizes,train_loss,color='r',label='training')
plt.plot(train_sizes,test_loss,color='g',label='cross_validation')
plt.xlabel('size')
plt.ylabel('accuracy')
plt.legend()
plt.show()

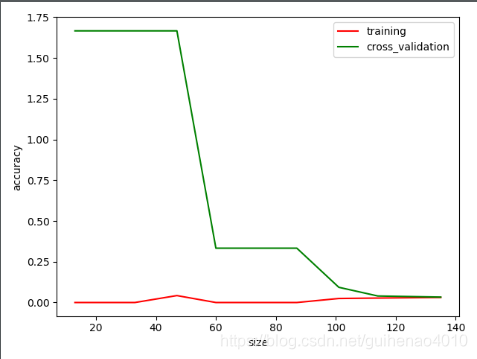
總結：

學習曲線Learning Curve：評估樣本量和指標的關係
驗證曲線validation Curve：評估引數和指標的關係