膨脹、腐蝕、開、閉運算——數字影象處理中的形態學
轉自:https://blog.csdn.net/welcome_xu/article/details/6694985
膨脹、腐蝕、開、閉運算是數學形態學最基本的變換。
本文主要針對二值影象的形態學
膨脹:把二值影象各1畫素連線成分的邊界擴大一層(填充邊緣或0畫素內部的孔);
腐蝕:把二值影象各1畫素連線成分的邊界點去掉從而縮小一層(可提取骨幹資訊,去掉毛刺,去掉孤立的0畫素);
開:先腐蝕再膨脹,可以去掉目標外的孤立點
閉:先膨脹再腐蝕,可以去掉目標內的孔。
以下參考論文:《數學形態學在影象處理中的應用》
二值形態學
數學形態學中二值影象的形態變換是一種針對集合的處理過程。
其形態運算元的實質是表達物體或形狀的集合與結構元素間的相互作用,結構元素的形狀就決定了這種運算所提取的訊號的形狀資訊。形態學影象處理是在影象中移動一個結構元素,然後將結構元素與下面的二值影象進行交、並等集合運算。
基本的形態運算是腐蝕和膨脹。
在形態學中,結構元素是最重要最基本的概念。結構元素在形態變換中的作用相當於訊號處理中的“濾波視窗”。用B(x)代表結構元素,對工作空間E中的每一點x,腐蝕和膨脹的定義為:
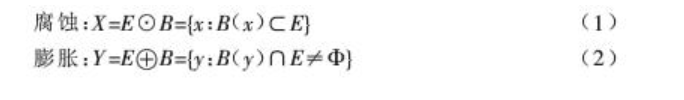
用B(x)對E進行腐蝕的結果就是把結構元素B平移後使B包含於E的所有點構成的集合。
用B(x)對E進行膨脹的結果就是把結構元素B平移後使B與E的交集非空的點構成的集合。
先腐蝕後膨脹的過程稱為開運算。它具有消除細小物體,在纖細處分離物體和平滑較大物體邊界的作用。
先膨脹後腐蝕的過程稱為閉運算。它具有填充物體內細小空洞,連線鄰近物體和平滑邊界的作用。
可見,二值形態膨脹與腐蝕可轉化為集合的邏輯運算,演算法簡單,適於並行處理
因此,很多學者結合自己的應用實際,提出了一系列的改進演算法。
如樑勇提出的用多方位形態學結構元素進行邊緣檢測演算法既具有較好的邊緣定位能力,又具有很好的噪聲平滑能力。
許超提出的以最短線段結構元素構造準圓結構元素或序列結構元素生成準圓結構元素相結合的設計方法,用於骨架的提取,可大大減少形態運算的計算量,並可同時滿足尺度、平移及旋轉相容性,適於對形狀進行分析和描述。
