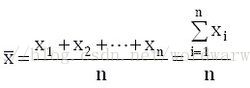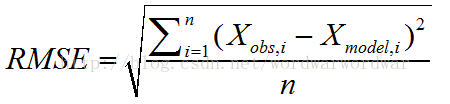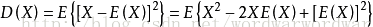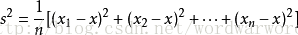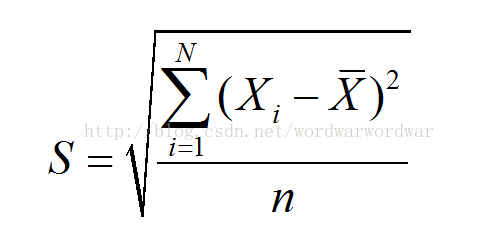1 均值

均值表示訊號中直流分量的大小，用E(x)表示。對於高斯白噪聲訊號而言，它的均值為0，所以它只有交流分量。

2 均值的平方

均值的平方，用{E(x)}^2表示，它表示的是訊號中直流分量的功率。

3 均方值

均方值表示訊號平方後的均值，用E(x^2)表示。均方值表示訊號的平均功率。訊號的平均功率 = 訊號交流分量功率 + 訊號直流分量功率

4 均方根值

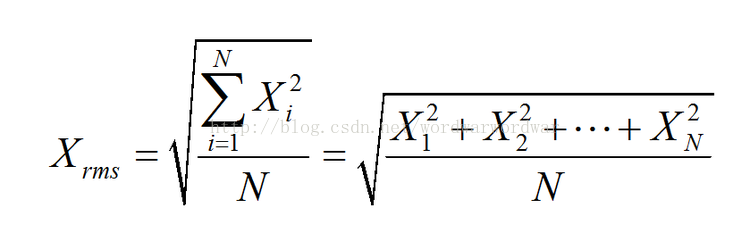
5 均方差

均方差（mean square error），用MSE表示。均方差是各資料偏離真實值的距離平方和的平均數，也即誤差平方和的平均數，計算公式形式上接近方差，它的開方叫均方根誤差，均方根誤差才和標準差形式上接近。均方差有時候被認為等同於方差

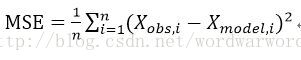
6 均方根誤差       

均方根誤差用RMSE（root mean square error）表示。它是觀測值與真值偏差的平方和觀測次數n比值的平方根，在實際測量中，觀測次數n總是有限的，真值只能用最可信賴（最佳）值來代替.方根誤差對一組測量中的特大或特小誤差反映非常敏感，所以，均方根誤差能夠很好地反映出測量的精密度。均方根誤差有時候被認為是標準差

6 方差

方差用variance或deviation 或Var表示。 方差描述訊號的波動範圍，表示訊號中交流分量的強弱，即交流訊號的平均功率。

      或用公式表示為

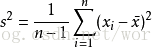
注意上面除以的是n-1，只有這樣由樣本值估計出的方差才是無偏的，即上面式子的期望才是X的方差。但是有的地方也有用除以n來表示方差，只不過這樣求出的結果不是方差的無偏估計，計算結果的數學期望並不是X的方差，而是X方差的

7 標準差

標準差（Standard Deviation）用σ表示，有的時候標準差又可以被稱為均方根誤差RMSE。 標準差是各資料偏離平均數的距離的平均數，它是離均差平方和平均後的方根，用σ表示，標準差能反映一個數據集的離散程度。

標準差σ， 反映了測量資料偏離真實值的程度，σ越小，表示測量精度越高，因此可用σ作為評定這一測量過程精度的標準。

有了方差為什麼要使用標準差？標準差比方差有什麼優勢？

因為方差與我們要處理的資料的量綱是不一致的，雖然能很好的描述資料與均值的偏離程度，但是處理結果是不符合我們的直觀思維的。 
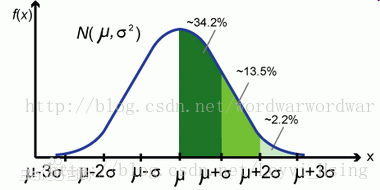
舉個例子：一個班級裡有60個學生，平均成績是70分，標準差是9，方差是81，成績服從正態分佈，那麼我們通過方差不能直觀的確定班級學生與均值到底偏離了多少分，通過標準差我們就很直觀的得到學生成績分佈在[61,79]範圍的概率為0.6826，即約等於下圖中的34.2%*2 。

總結：

（1）總的來說，均方差，均方根誤差和方差，標準差是不能夠等同的，儘管它們的公式相似。我們需要從真實值和均值之間的關係來區分它們

（2）對於方差和標準差而言，它們反映的是資料序列與均值的關係。

（3）對於均方差和均方根誤差而言，它們反映的是資料序列與真實值之間的關係。