題目連結：https://code.google.com/codejam/contest/3324486/dashboard#s=p2

題目：

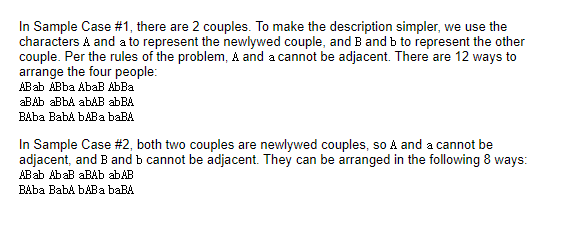
思路：

程式碼實現如下：

 1 #include <set>
 2 #include <map>
 3 #include <deque>
 4 #include <queue>
 5 #include <stack>
 6 #include <cmath>
 7 #include <ctime>
 8 #include <bitset>
 9
 
 #include <cstdio>
10 #include <string>
11 #include <vector>
12 #include <cstdlib>
13 #include <cstring>
14 #include <iostream>
15 #include <algorithm>
16 using namespace std;
17 
18 typedef long long LL;
19 typedef pair<LL, LL> pLL;
20 typedef pair<LL, int
 
> pli;
21 typedef pair<int, LL> pil;;
22 typedef pair<int, int> pii;
23 typedef unsigned long long uLL;
24 
25 #define lson rt<<1
26 #define rson rt<<1|1
27 #define lowbit(x) x&(-x)
28 #define  name2str(name) (#name)
29 #define bug printf("*********\n")
30 #define
 
 debug(x) cout<<#x"=["<<x<<"]" <<endl
31 #define FIN freopen("D://code//in.txt", "r", stdin)
32 #define IO ios::sync_with_stdio(false),cin.tie(0)
33 
34 const double eps = 1e-8;
35 const int mod = 1000000007;
36 const int maxn = 2e5 + 7;
37 const double pi = acos(-1);
38 const int inf = 0x3f3f3f3f;
39 const LL INF = 0x3f3f3f3f3f3f3f3fLL;
40 
41 int t, n, m;
42 LL A[maxn], inv[maxn];
43 
44 LL Mod_Pow(LL x, int n) {
45     LL res = 1;
46     while(n) {
47         if(n & 1) res = res * x % mod;
48         x = x * x % mod;
49         n >>= 1;
50     }
51     return res;
52 }
53 
54 void init() {
55     A[0] = 1;
56     for(int i = 1; i < maxn; i++) A[i] = (A[i-1] * i) % mod;
57     inv[maxn-1] = Mod_Pow(A[maxn-1], mod - 2);
58     for(int i = maxn - 2; i >= 0; i--) {
59         inv[i] = inv[i+1] * (i + 1) % mod;
60     }
61 }
62 
63 int Com(int n, int m) {
64     if(n < 0 || m < 0 || m > n) return 0;
65     if(m == 0 || m == n) return 1;
66     return ((A[n] * inv[n-m] % mod) * inv[m]) % mod;
67 }
68 
69 int main() {
70 #ifndef ONLINE_JUDGE
71     FIN;
72 #endif
73     init();
74     int icase = 0;
75     scanf("%d", &t);
76     while(t--) {
77         scanf("%d%d", &n, &m);
78         LL sum = 0;
79         for(int i = 0; i <= m; i++) {
80             if(i % 2 == 0) {
81                 sum = (sum + ((Com(m, i) * Mod_Pow(2, i) % mod) * A[2 * n - i]) % mod) % mod;
82             } else {
83                 sum = (sum - ((Com(m, i) * Mod_Pow(2, i) % mod) * A[2 * n - i]) % mod + mod) % mod;
84             }
85         }
86         printf("Case #%d: %lld\n", ++icase, sum % mod);
87     }
88     return 0;
89 }