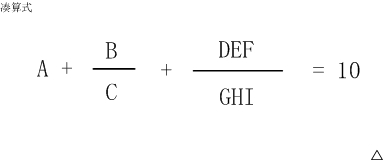
這個算式中A~I代表1~9的數字，不同的字母代表不同的數字。

比如：
6+8/3+952/714 就是一種解法，
5+3/1+972/486 是另一種解法。
這個算式一共有多少種解法？

注意：你提交應該是個整數，不要填寫任何多餘的內容或說明性文字。

演算法思想：將A-I所代表的數字進行全排列，然後進行檢檢視看是否符合等式。

資料域：

1.private static int[] visited;

主要是用來表示資料是否被訪問過（0表示資料尚未被訪問過，1表示資料已經被訪問過了）。

2.private static double[] save;

用來儲存資料。

3.private static int sum;
   用來計數，統計符合該等式的情況數。

方法：

1.資料的初始化

private static void init() {
        visited=new int[9];
        for(int i=0;i<9;i++) {
            visited[i]=0;//0表示尚未被訪問,1表示已經被訪問過了
        }
        save=new double[9];
    }

2.檢測是否滿足等式

private static boolean check() {
        double def=save[3]*100+save[4]*10+save[5];
        double ghi=save[6]*100+save[7]*10+save[8];
        double left=save[0]+save[1]/save[2]+def/ghi;
        if(left==10) {
            return true;
        }
        return false;
    }

3.進行深度搜索

private static void dfs(int step) {
        if(step>8) {
            if(check()==true) {
                sum++;
            }
            return;//注意return不可寫在if語句裡面
        }
        
        else {
            for(int i=1;i<10;i++) {
                if(visited[i-1]==0) {//當前的數字沒有被訪問
                    save[step]=i;
                    visited[i-1]=1;//設定當前數字狀態為已經被訪問過了
                    dfs(step+1);
                    visited[i-1]=0;//回溯
                }
            }
        }
    }

注意：儲存資料的元素型別應該是double型，而不應該是int型。

答案：29