題目連結：洛谷-P3379

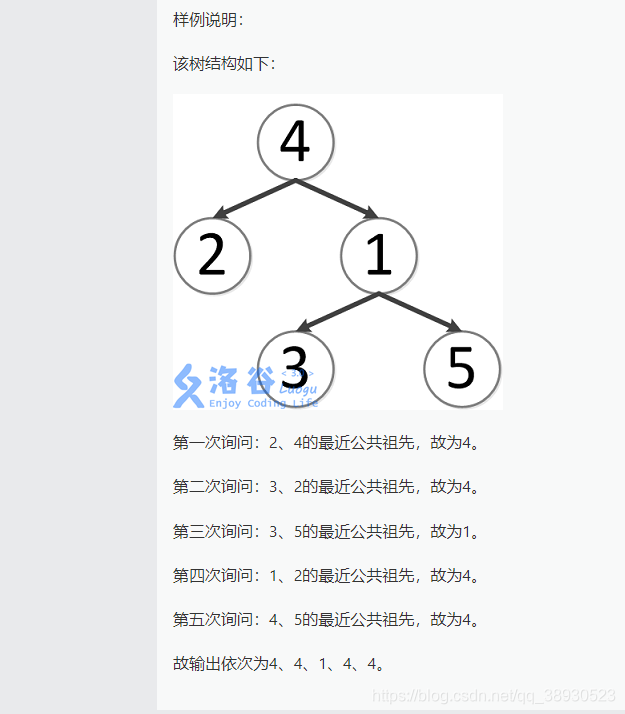
如題，給定一棵有根多叉樹，請求出指定兩個點直接最近的公共祖先。

思路

這是一個裸的LCA問題，即求書上兩個節點的最近公共祖先。
我們可以用樹上倍增來做；

當然，在做之前我們假設不知道該演算法。那麼我們如何來做這種型別的題目呢？
顯然，我們可以用暴力來做，找到兩點的最近公共祖先，我們可以用前向星存雙向邊，然後依次儲存每個點到的根的路徑。然後找到最先同時出現在兩條路徑的公共點即可；
顯然，這樣是可做的。但是這樣做，考慮到:
1.當書的深度非常大
2.當最壞情況樹退化為一條鏈式
3.當詢問次數非常多的時候。
以上，無論那種情況，起步都是O（N^2）的複雜度,顯然，這樣的做法並不夠優秀，所以我們引入倍增的做法，它可以NlogN的時間複雜度完成預處理，每次詢問LogN的時間給出回答；

倍增演算法：所謂倍增，就是按2的倍數來增大，也就是跳 1,2,4,8,16,32 …… 不過在這我們不是按從小到大跳，而是從大向小跳，即按……32,16,8,4,2,1來跳，如果大的跳不過去，再把它調小。這是因為從小開始跳，可能會出現“悔棋”的現象。拿 5為例，從小向大跳，5≠1+2+4,所以我們還要回溯一步，然後才能得出5=1+4；而從大向小跳，直接可以得出5=4+1。這也可以拿二進位制為例，5(101)，從高位向低位填很簡單，如果填了這位之後比原數大了，那我就不填，這個過程是很好操作的。

lca的倍增做法就是 用一個fa[i][j]陣列 來儲存 i 節點的 2^j 倍父親是哪個節點； 這樣做每次都是2倍區間查詢，所以可以在logN的時間給出答案；

我們先跑一遍dfs， 初始化 深度 d陣列 ， 初始化 fa[i][0] 。 跑一遍dfs後，d陣列儲存的就是每個節點的深度（預設根節點深度為1）. fa陣列儲存的就是 fa[i][0] 就是 每個節點儲存的都是他父親節點的編號；

跑完dfs，我們需要對全域性fa進行賦值； 這裡用到的轉移方程是
fa[i][j] = fa[fa[i][j-1]][j-1] 。
比如(畫的比較醜)

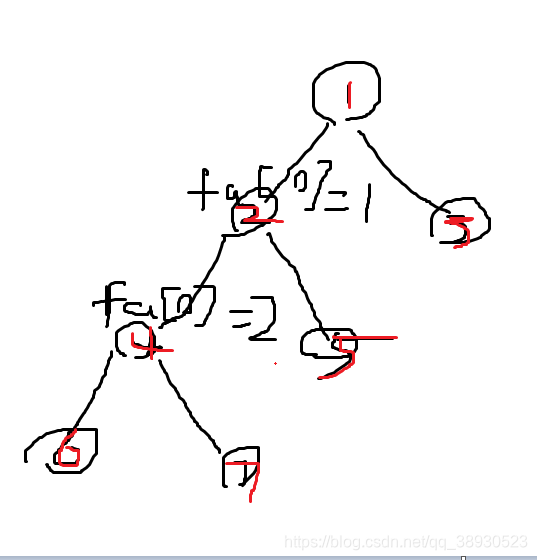
2節點的 fa[2][0] 為 1 。 就是 2節點 的 (2^0 = 1)的父親為 1
4節點的fa[4][0]為 2。 就是 4號節點的父親為 2

要求 fa4 我們可以表示為 fa[fa[4][0]][0]， 就是4號父親的父親， 這樣遞推上去，就可以的出每個fa；

完成這步之後，我們剩下就是求Lca了；

先把x節點和y節點挪到同一層， 挪到同一層後， 若 x == y 代表一開始 x 就是y的祖先或者y是x的祖先；

若 x != y， 則 我們找到最深的滿足 fa[x][i] != fa[y][i] ；
然後返回x的父親節點即可。
至此，我們的演算法就結束了；

lca倍增學習：很明白的lca教程

易錯點

1.建樹用前向星建， 注意邊數為n-1條，雙向邊，則應該開闢MAX_N * 2空間
2.此題輸入輸出量很大， 用scanf和printf輸入輸出；
3.這題好像卡常數的樣子？ 初始化head和深度d的時候用迴圈初始化，memset會超時！

AC程式碼

#include <bits/stdc++.h>
using namespace std;

#define MAX_N 500050

int head[MAX_N], cnt = 0, d[MAX_N], fa[MAX_N][30];

struct Node{
    int to, next;
}edge[MAX_N * 2];

void add(int x, int y)
{
    edge[cnt].to = y;
    edge[cnt].next = head[x];
    head[x] = cnt++;
}

void dfs(int v)
{
    for(int i = head[v]; i != -1; i = edge[i].next)
    {
        int k = edge[i].to;
        if(d[k] == 0)
        {
            d[k] = d[v] + 1;
            fa[k][0] = v;
            dfs(k);
        }
    }
}

int lca(int x, int y)
{
    if(d[x] < d[y])
    {
        swap(x, y);
    }
    for(int i = 20; i>=0; i--)
    {
        if(d[fa[x][i]] >= d[y])
            x = fa[x][i];
    }
    if(x == y)
        return x;
    for(int i = 20; i >= 0; i--)
    {
        if(fa[x][i] != fa[y][i])
        {
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[x][0];
}

int main()
{
    int n, m, r;
    scanf("%d %d %d", &n, &m, &r);
    for(int i = 1; i<=n; i++)
    {
        head[i] = -1;
        d[i] = 0;
    }
    for(int i = 0; i<n-1; i++)
    {
        int x, y;
        scanf("%d %d", &x, &y);
        add(x, y);
        add(y, x);
    }
    fa[r][0] = 0, d[r] = 1;
    dfs(r);
    for(int i = 1; i<=20; i++)
    {
        for(int j = 1; j<=n; j++)
        {
            fa[j][i] = fa[fa[j][i-1]][i-1];
        }
    }
    while(m--)
    {
        int x, y;
        scanf("%d %d", &x, &y);
        printf("%d\n", lca(x, y));
    }
    return 0;
}