1.最近公共祖先的定義：

• 在一棵沒有環的樹上，每個節點肯定有其父親節點和祖先節點，而最近公共祖先，就是兩個節點在這棵樹上深度最大的公告的祖先節點。
• 你的父親是你的祖先，而LCA還可以將自己視為祖先節點。
• 舉個例子吧，如下圖所示：LCA(3,5)=1,LCA(2,3)=4,LCA(1,5)=1;

2.如何求LCA

• 我們先想暴力的方法：

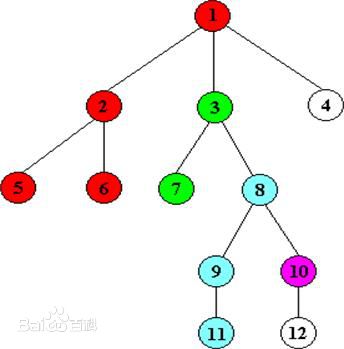
• 舉個例子：對於5和11的LCA是1;
• 先DFS遍歷一遍，找出每個點的深度，然後從要求的兩個點中深度較大的點(11)開始往上跳，跳到和深度較小的點(5)的相同深度(8)，發現還不是同一個點，於是兩個點一起跳，直到是同一個點(1)，這個點就是它們的最近公共祖先。

3.如何優化

• 首先這個暴力的方法慢在哪裡？就是在往上跳的時候只能一個一個的跳，但是有的時候並不需要跳那麼多下，所以只要每次可以多跳一點，就能節省時間了。
• 我們這裡之講解樹上倍增法：
• 原理（自己理解的）：因為每個十進位制數都可以轉化成二進位制，也就是說每一個十進位制數都可以由幾個2的冪之和來組成。如：10(2)=1010，10=2^3+2^1。17(2)=10001，17=2^4+2^1。所以對於每次要跳的步數都可以拆成幾個2的冪之和，就可以每次先從大的2的次方跳，超過了就縮小次方，然後一直重複知道跳到了。
• 具體實現方法：
• 預處理 O(nlogn)：用f[x][k]表示x的跳2^k步的祖先，所以每個x的爸爸就是f[x][0];對於求f[x][k]，每個點x的跳2^k步的祖先就是它跳2^(k-1)步的祖先再跳2^(k-1)步的祖先，即f[x][k]=f[x][f[x][k-1]][k-1];這類似於動態規劃的過程，“階段”就是結點的深度。因此，就DFS便歷，求出f[x][0]，然後再計算f陣列所有的值。
• 求LCA O(logn)：

1. 設deep[x]表示x的深度。不妨設deep[x]>=deep[y]（否則，swap(x,y)）;
2. 不斷跳，把x跳到和y一樣的深度。具體說：就是依次嘗試x向上走2^(logn)……2^3,2^2,2^1步，若深度還比y大，就令x=f[x][k];
3. 若此時x==y，說明已經找到了LCA，即y。
4. 如果x！=y，那就讓x和y一起往上跳，並保證沒有跳過。具體說：就是依次嘗試x和y向上走2^(logn)……2^4，2^3，2^2，2^1步，若f[x][k]！=f[y][k](還沒跳到一起)，就讓x=f[x][k],y=f[y][k];
5. 那麼必定x和y的LCA就是f[x][0]了;

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
int n,m,root,k,head[500001],deep[500001],f[500001][21];
struct zhzs
{
    int to,next;
}edge[1000001];
inline void add(int u,int v)
{
    edge[++k].to=v;
    edge[k].next=head[u];
    head[u]=k;
}
void dfs(int t,int baba)
{
    deep[t]=deep[baba]+1;
    f[t][0]=baba;
    for(register int i=1;(1<<i)<=deep[t],i<=20;++i)//一定要記住不能超過整個樹的祖先
    f[t][i]=f[f[t][i-1]][i-1];
    for(register int i=head[t];i;i=edge[i].next)
    if(edge[i].to!=baba)
    dfs(edge[i].to,t);
}
int lca(int x,int y)
{
    if(deep[x]<deep[y])
    swap(x,y);
    for(register int i=20;i>=0;--i)
    if(deep[x]-(1<<i)>=deep[y])
    x=f[x][i];
    if(x==y)
    return x;
    for(register int i=20;i>=0;--i)
    if(f[x][i]!=f[y][i])
    {
        x=f[x][i];
        y=f[y][i];
    }
    return f[x][0];
}
int main()
{
    scanf("%d%d%d",&n,&m,&root);
    int x,y;
    for(register int i=1;i<=n-1;++i)
    {
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);//鏈式鄰接表存邊
    }
    dfs(root,0);
    for(register int i=1;i<=m;++i)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));
    }
    return 0;
}