廢話不多說，總而言之就是下面幾步：

1 計算所有的 Ei

2 尋找第一個違反KKT的變數

3尋找第二個Ei差值的變數

4更新alpha和b，並重新計算所有的Ei

下面舉個詳細的例子，首先這是樣本的分佈圖，非線性

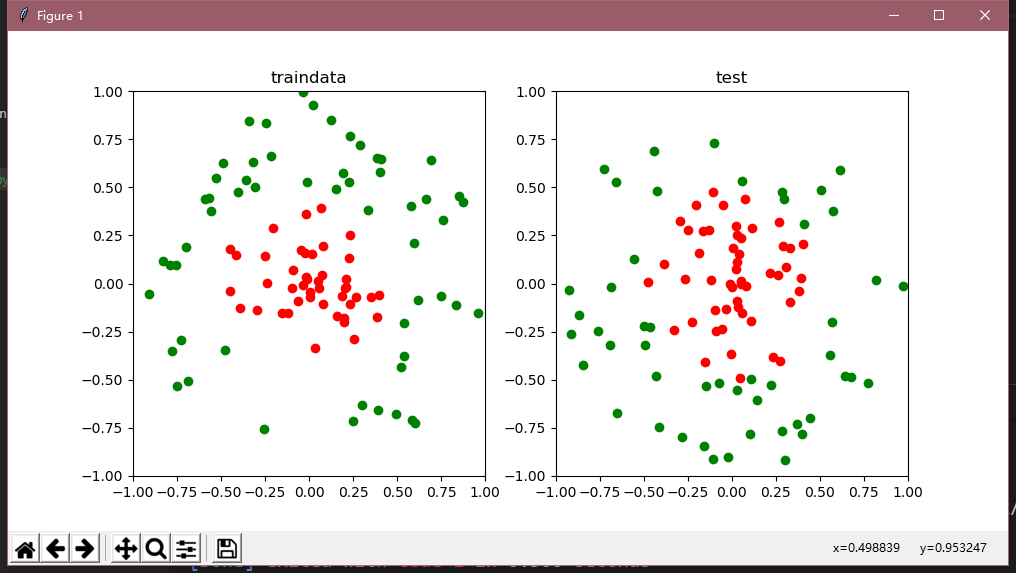
其次這是識別後的圖以及正確率（正確率這個需要調參，太麻煩了，所以我就這樣了）

 

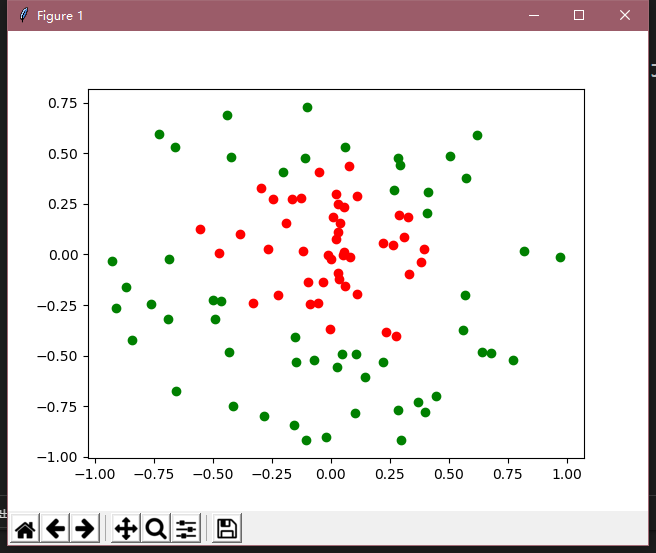
詳細程式碼如下：

import numpy as np import os.path import re import matplotlib.pyplot as plt os.chdir('F:/machine_learning/SVM/')

def loadData(filename): dataMat = [] labelMat = [] row = [] fr = open(filename) for line in fr.readlines(): lineArr = re.split("\s+", line.strip()) for cols in range(len(lineArr) - 1): row.append(float(lineArr[cols])) dataMat.append(row) row = [] labelMat.append(float(lineArr[-1])) return np.array(dataMat), np.array(labelMat)

# X:訓練集 i:樣本序號 sigmar:高斯核的頻寬,返回的是第j個樣本與所有樣本的高斯核 # 即 K(i, j) {i=1, m} m為樣本大小，sigmar為選擇高斯核的引數，不選擇不起作用 def Kernel(X, j, sigmar, ker='Rbf'): m, n = np.shape(X) K = np.mat(np.zeros((m, 1))) if(ker == 'line'): return X*X[j].T else: for i in range(m): deta = np.mat(X[i] - X[j]) K[i] = deta * deta.T K = np.exp(K/(-2*sigmar**2)) return K

def KernelJ(X, Xj, sigmar, ker='Rbf'): m, n = np.shape(X) K = np.mat(np.zeros((m, 1))) if(ker == 'line'): return X*Xj.T else: for i in range(m): deta = np.mat(X[i] - Xj) K[i] = deta * deta.T K = np.exp(K/(-2*sigmar**2)) return K

# 輸入的引數有資料，懲罰引數C，高斯核頻寬sigmar，容忍度epsilon,最大迭代次數 class SVM: def __init__(self, dataT, labelT, C=1, sigmar=0.1, ker='Rbf', epsilon=0.5, maxIter=100): self.X = dataT self.C = C self.sigmar = sigmar self.ker = ker self.epsilon = epsilon self.maxIter = maxIter self.m = np.shape(dataT)[0] self.n = np.shape(dataT)[1] self.Y = labelT.reshape((self.m, 1)) self.b = 0 self.alpha = np.mat(np.zeros((self.m, 1))) self.K = np.mat(np.zeros((self.m, self.m))) self.E = np.mat(np.zeros((self.m, 1))) for i in range(self.m): self.K[:, i] = Kernel(self.X, i, sigmar, ker)  
# 計算Ei,np.multiply是對應位置相乘，並不是矩陣乘法，和陣列乘法類似 def calError(self): for i in range(self.m): gxi = float(np.multiply(self.alpha, np.mat(self.Y)).T* self.K[:, i])+self.b self.E[i] = gxi - self.Y[i]  
# 選擇第二個alpha並返回j def selectJ(self, i): maxDeta = -1 maxJ = 0 for k in range(self.m): deta = np.abs(self.E[i] - self.E[k]) if(deta > maxDeta): maxDeta = deta maxJ = k return maxJ

def clipAlp(self, j, H, L): if(self.alpha[j] > H): self.alpha[j] = H if(self.alpha[j] < L): self.alpha[j] = L
 
# 計算內迴圈，引數i為選取的第一alpha，但是並未判斷，所有的判斷都在內迴圈 def innerCir(self, i): # yi*gxi - 1=yi*Ei # 雖然只有兩個式子，但包含了三個KKT條件均違反的情況 # E的更新在b之後，切記不要記錯順序 if((self.alpha[i] < self.C and self.Y[i]*self.E[i] <(-self.epsilon)) or (self.alpha[i] > 0 and self.Y[i]*self.E[i] > (self.epsilon))): j = self.selectJ(i) alphaIOld = self.alpha[i].copy() alphaJOld = self.alpha[j].copy() if(self.Y[i] == self.Y[j]): L = np.maximum(0, alphaIOld+alphaJOld - self.C) H = np.minimum(self.C, alphaIOld+alphaJOld) else: L = np.maximum(0, alphaJOld - alphaIOld) H = np.minimum(self.C, self.C + alphaJOld - alphaIOld) if(L == H): return 0 eta = self.K[i, i] + self.K[j, j] - 2 * self.K[i, j] self.alpha[j] += self.Y[j]*(self.E[i] - self.E[j])/eta self.clipAlp(j, H, L) if(abs(self.alpha[j] - alphaJOld) < 0.0001): return 0 self.alpha[i] += self.Y[i]*self.Y[j]*(alphaJOld - self.alpha[j]) b1 = self.b-self.E[i]-self.Y[i]*self.K[i, i]*(self.alpha[i] - alphaIOld)-self.Y[j]*self.K[i, j]*(self.alpha[j]-alphaJOld) b2 = self.b-self.E[j]-self.Y[i]*self.K[i, j]*(self.alpha[i] - alphaIOld)-self.Y[j]*self.K[j, j]*(self.alpha[j]-alphaJOld) self.b = (b1 + b2)/2 self.calError() return 1 else: return 0

# 計算外迴圈 def outCir(self): alphachanged = 0 iter = 0 boundValue = True # 所有的alpha都處於邊界值 self.calError() # 剛開始遍歷所有樣本，之後遍歷（0，C）之間的alpha，最後再遍歷一次所有樣本 while((alphachanged > 0 or boundValue) and (iter < self.maxIter)): alphachanged = 0 if(boundValue): for i in range(self.m): alphachanged += self.innerCir(i) iter += 1 else: # 陣列乘法是對應位置相乘，和矩陣不一樣 nonBound = np.nonzero( (self.alpha.A > 0)*(self.alpha.A < self.C))[0] for i in nonBound: alphachanged += self.innerCir(i) iter += 1 if(boundValue): boundValue = False elif(alphachanged == 0): boundValue = True  
def pridict(self, testData, testLabel): self.outCir() m, n = np.shape(testData) label = [] k = 0 for i in range(m): Fxi = np.multiply(self.alpha, self.Y).T*KernelJ(self.X, testData[i], self.sigmar) + self.b if(Fxi <= 0): label.append(-1) else: label.append(1) for i in range(m): if(int(testLabel[i]) == int(label[i])): k += 1 accuracy = float(k)/m positive = [] negative = [] for i in range(m): if(label[i] == 1): positive.append(testData[i]) else: negative.append(testData[i]) positive = np.array(positive) negative = np.array(negative) plt.scatter(positive[:, 0], positive[:, 1], c='r', marker='o') plt.scatter(negative[:, 0], negative[:, 1], c='g', marker='o') plt.show() print("accuracy=%f" % accuracy)

if __name__ == "__main__": trainData, trainLabel = loadData("trainData.txt") svm = SVM(trainData, trainLabel) testData, testLabel = loadData("testData.txt") svm.pridict(testData, testLabel) 可能格式複製有點不對，詳細的資料檔案可以去我的github下載，排版很low我知道，就醬紫吧：https://github.com/SagacitySucura/Machine_Learning/tree/master/SVM