#include<iostream>
#include<cstdio>
#include<cstring>
 
using namespace std;
 
void print_subset(int n, int *A, int cur) {
    for(int i = 0; i < cur; ++i) {
        printf("%d ", A[i]);
    }
    printf("\n");
 
 
    int s = cur ? A[cur - 1] + 1:0; 
    for(int i = s; i < n; ++i) {
        A[cur] 
 
= i;
        print_subset(n, A, cur + 1);
    }
}
 
int main() {
    int n;
    int A[4]={0,1,2,3};
    while(scanf("%d", &n) == 1) {
        print_subset(n, A, 0);
    }
    return 0;
}

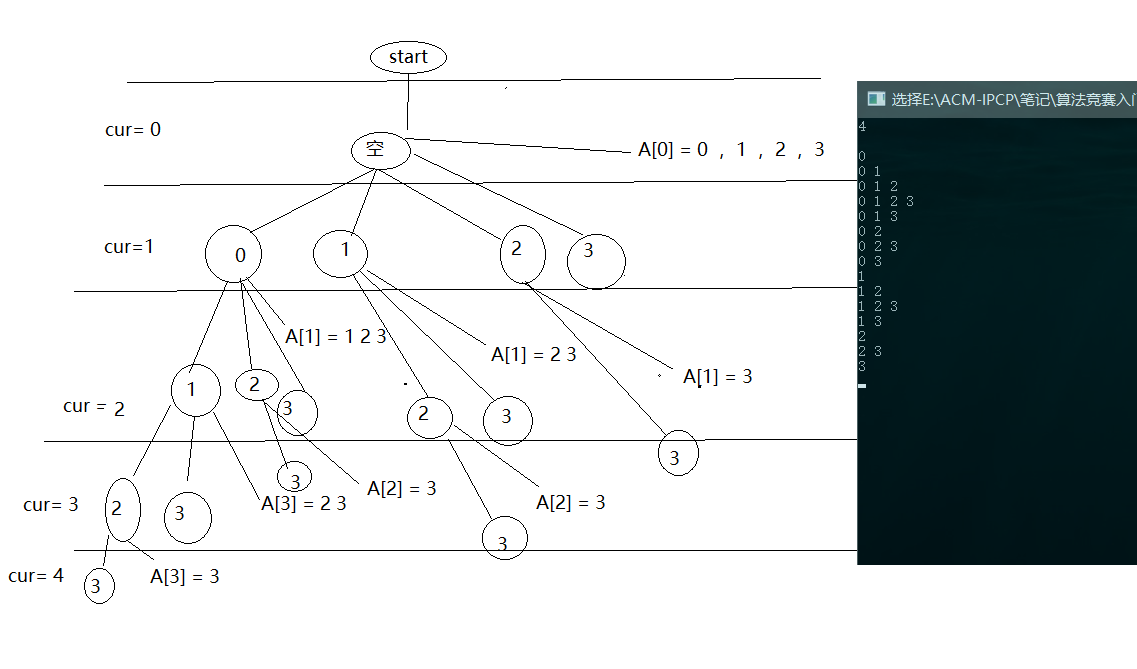
(參考https://blog.csdn.net/qq_30388187/article/details/76982403)