子集構造法NFA轉換成DFA
教材《編譯原理》(龍書)第2版
關於這部分,教材在P94頁有說明,但是我覺得不容易理解,下面通過兩個例題來理解一下。
例題一:
這一題比較簡單,我們直接從答案找解題方法
第一步:要根據NFA畫出這個表格,可能有些模糊,表頭分別為I,Ia,Ib,狀態(是對I這一列自定義的狀態名稱)
下面我們來說一下第一行的三項如何得出:(S就是開始狀態)
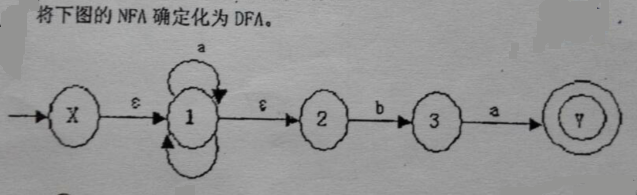
先以S開始,經過任意個ε得到的結點就是第一個I,這道題就是{X, 1,2},
然後將{X,1,2}中的每一個字元經過a (中間可以有ε)後得到的結點加起來,
X的Ia={1,2}, 1的Ia={1,2}, 2的Ia是空集,所以這一行的Ia={1,2}。
後面的Ib也是一樣,只不過是經過b後得到的結點的集合.
也就是說I的第一行第一列{X, 1,2},是從開始符號經過ε得到的集合,而Ia,Ib是集合中每個結點分別經過a,b得到的集合的並集。
第二行的第一列I,是第一行的Ia,如果仔細觀察,就可以發現:第一列都是將前面的Ia和Ib作為I計算新的Ia和Ib。
當然要注意重複的狀態集合,就沒有必要再作為I寫一次了。
直到把所有的新狀態都作為I寫一遍,這個表就完成了。
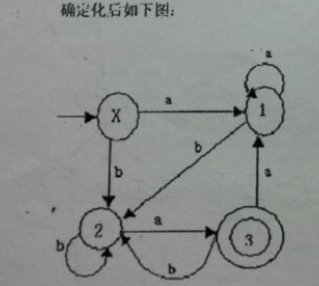
第二步:根據表格畫出DFA
將這些集合依次標號,這道題是{X,1,2}為X,{1,2}為1, {1,2,3}為2,{1,2,Y}為3,根據上面那個表就可以把圖畫出來了。
關於箭頭指向和箭頭的值,都要從每一行的三項來看,比如第一行,如果把集合換成自定義的狀態編號就是
I Ia Ib
X 1 2
意思就是X經過a到達狀態1,X經過b到達狀態2。
並且由於Y在NFA中是一個接受狀態,在表格的狀態3中也有Y,所以3是接受狀態。
例題二:
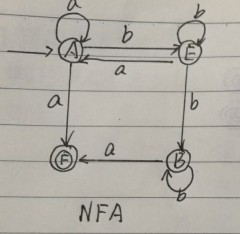
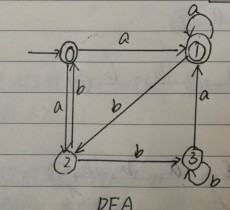
將下圖NFA轉換成DFA
這一個NFA中不含有ε,一開始我也不知該怎麼做,和上一題有一些小區別,是我同學給我講的,如果不對,就不要借鑑了。
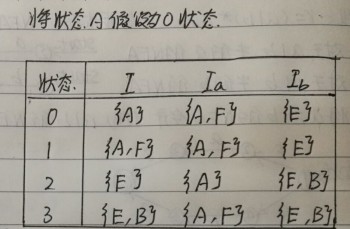
區別就在於,每一個集合不再是把所有經過a,b的結點都寫入,而是隻寫第一個經過的結點,例如第一行的Ib,從A經過b的所有結點事{E,B},但是隻記錄了一個E。
最後的結果是:
---------------------
作者:elice_
來源:CSDN
原文:https://blog.csdn.net/elice_/article/details/80550413