二維旋轉公式
阿新 • • 發佈:2018-11-21
二維旋轉公式
ros的tf工具包可以很方便的實現任意座標系之間的座標轉換。但是,如果只是想簡單的測試想法,而又不想編寫過於龐雜的程式碼,考慮自己寫二維旋轉的函式。而與二維旋轉問題對偶的另一個問題便是二維座標系旋轉變換。這兩個問題的形式基本一樣,只是旋轉的角度相差一個負號。就是這個容易搞混,所以做個筆記,以備查用。
1. 二維旋轉公式(演算法)
而(此文只針對二維)旋轉則是表示某一座標點
某一座標系下繞原點逆時針(正向)旋轉角度
後得到新的座標點
。
推導:
假定
,
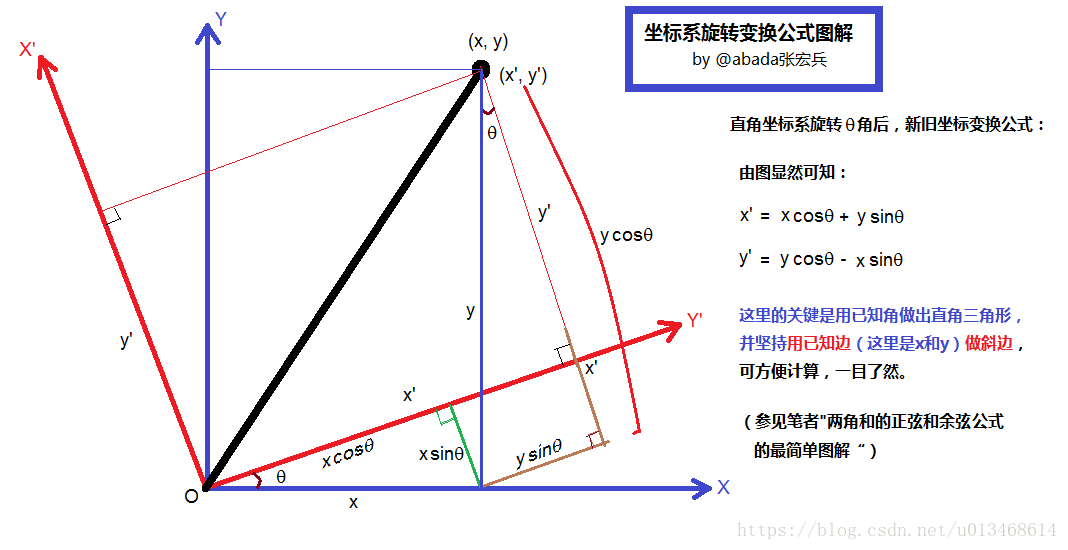
,如上圖有
(注意,上圖有幾處錯誤,座標軸邊上的
應改為
)。展開
可得:
矩陣形式為:
則二維旋轉矩陣為:
void Rotate2(double x1, double y1, double alpha, double& x2, double& y2)
{
x2 = x1 * cos(alpha) - y1 * sin(alpha);
y2 = x1 * sin(alpha) + y1 * cos(alpha);
}
2. 二維座標系旋轉變換
假設有一座標系
,經過逆時針(正向)旋轉角度
後,得到新的座標系
。得到原來座標系中的座標
在新座標系下的座標值被稱為座標系轉換。
所以二維座標旋轉變換矩陣為: