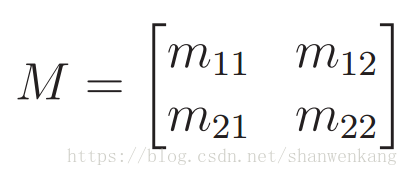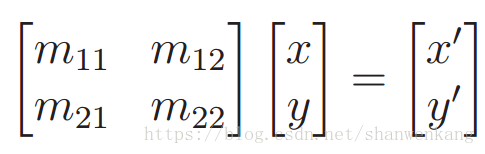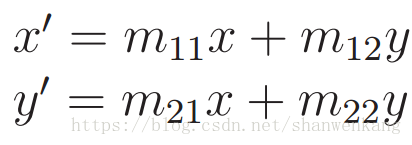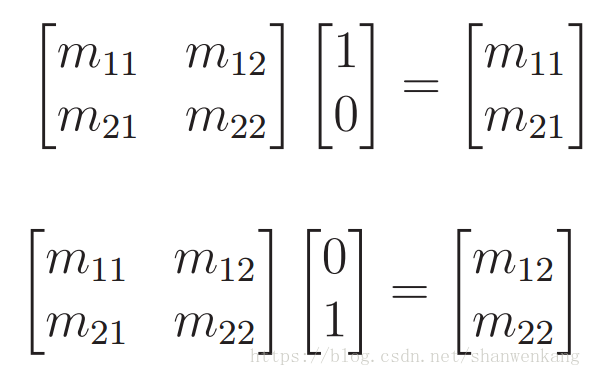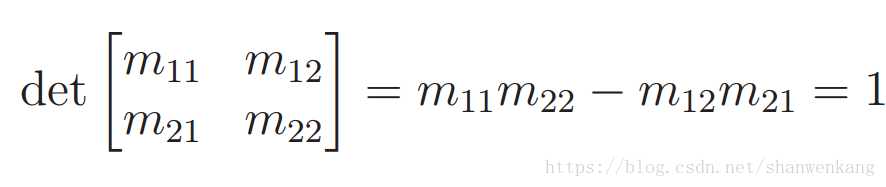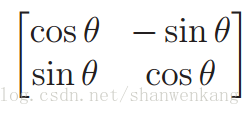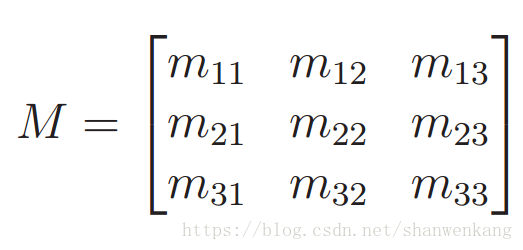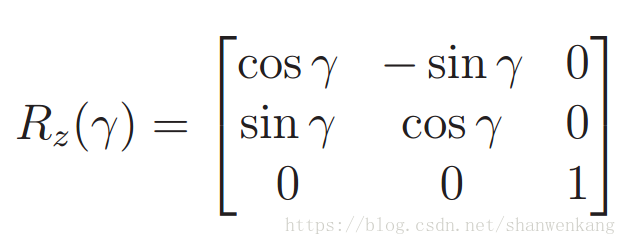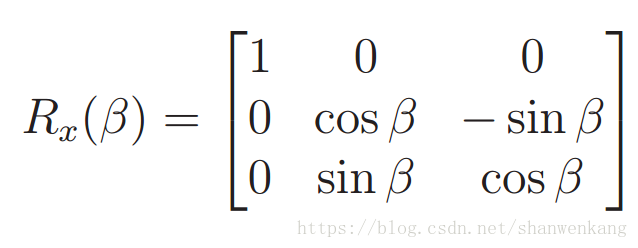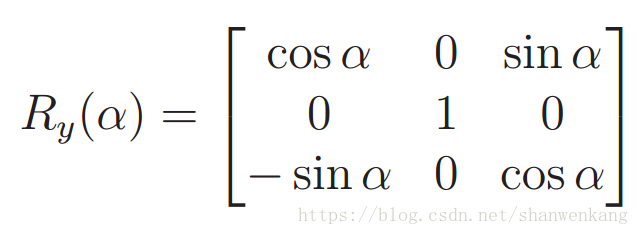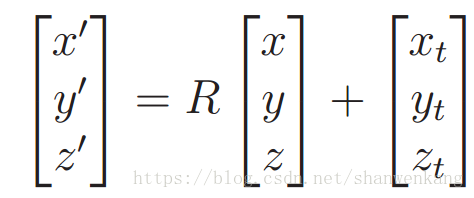Steven M. LaValle 的 Virtual Reality 這本書中講了關於幾何模型變換以及顯示的知識，跟網上的資料比這本書裡講的比較簡潔，於是想做一個總結。本部落格參考了《Virtual Reality》的中文譯版，翻譯與校驗人員: 上海交通大學媒體技術實驗室(http://medialab.sjtu.edu.cn) 

Part I

平移

考慮以下 3D 三角形
((x1, y1, z1), (x2, y2, z2), (x3, y3, z3))
頂點座標表示為通用常量。

設 xt，yt 和 zt 是分別沿 x，y 和 z 軸的我們想要改變的三角形位置量。 改變位置的操作稱為變換，由下式給出
(x1, y1, z1) → (x1 + xt, y1 + yt, z1 + zt)
(x2, y2, z2) → (x2 + xt, y2 + yt, z2 + zt)
(x3, y3, z3) → (x3 + xt, y3 + yt, z3 + zt)
其中 a→b 表示在變換之後 a 被 b 替換。

旋轉——2D

考慮一個 2D 虛擬世界，其中的點座標（x，y）。 你可以把它想象成我們最初的 3D 虛擬世界中的一個垂直平面。 現在考慮一個通用的 2x2 矩陣。

其中四項的每一個可以是任何實數。 我們看看當這個矩陣乘以點（x， y）後會發生什麼，當它被寫為列向量時。執行乘法，我們有
 

其中（x'，y'）是變換點。使用簡單的代數，矩陣乘法產生

假設我們放置兩個點（1,0）和（0,1）在平面上。它們分別位於 x 和 y 軸上，距離原點的距離（0，0）一個單位。使用向量空間，這兩點就是標準單位向量（有時寫為 i 和 j）。如果我們將它帶入矩陣乘法中可以得到：

這些特殊點只選擇 M 上的列向量。這意味著如果 M 應用於模型轉換，則 M 的每一列確切地表示每個座標軸是如何改變的，也就是說x軸變換成了（m11,m21）這個方向，y軸變換成了（m12,m22）這個方向。下圖說明了將各種矩陣 M 的變換效果。

對於上述M矩陣中只有一部分是有效的旋轉，因為為了確保模型不會被扭曲，要求M滿足下列條件：

1.沒有伸展的軸。
2.沒有剪下。
3.沒有映象。

為了滿足第一條規則，M 的列必須有單位長度

為了滿足第二條規則，必須保證轉換後的座標軸垂直。否則，會發生剪下。由於 M 的列表示軸是如何變換的，那麼此規則意味著它們的內部（點）積為零，也就是x軸的變換（m11,m21）與y軸的變換（m21,m22）垂直：

滿足第三條規則要求 M 的行列式是正數。當滿足前兩條規則後，唯一可能的行列式是 1（正常情況下）和-1（映象情況）。 因此，該規則意味著：

第一個約束條件表示每列必須都被選擇以使它每個元素位於一個以原點為中心的單位圓上。在標準的平面座標，我們通常將這個圓的方程寫作 x^2 +y^2 = 1，在極座標下可以得x = cosθ y = sinθ。我們用角度θ代替點的座標（x， y），令 m11=cosθ m21= sinθ，M可寫做：

這樣通過θ的變化（0~2π範圍內），就可以表示所有的 2D 旋轉。

接下來我們討論旋轉的自由度（DOF）。一開始的時候，矩陣 M 的四個元素是可以任意取值的，也就是說有 4 個自由度。第一個約束條件減少兩個自由度，第二個條件也減少一個自由度，第三個條件並沒有減少自由度，它只去掉了一半可能的變換，因為這些變換是另一半的映象翻轉。 最後， 我們得出結論， 2D 旋轉只有一個自由度， 由引數θ決定； 而且，這些旋轉都可以用單位圓的點來表示

旋轉——3D

現在我們嘗試將 2D 旋轉的模式擴充套件到三維空間中，旋轉矩陣的三維形式如下所示，包含 9 個元素：

因此，一開始 3D 旋轉有著 9 個自由度，同樣的，我們也要知道一個合法的 3D 旋轉需要哪些限制條件。首先，每一列必須保證是單位長度。例如，這就是說每一列中的元素必須落在單位球面上。因此，單位長度的限制將 DOF 減少到 6 個。然後，根據正交軸定理，取矩陣的任意兩列，它們的內積必須為 0。最後，為了避免映象出現，矩陣 M 的行列式要為 1，但這不減少自由度。

最後，我們得到了一系列滿足代數約束的矩陣，然而，和 2D 旋轉不同，它並不能用單位球面上的點來表示。我們只知道它有 3 個旋轉自由度，意味著它應該可以由 3 個獨立的引數來表示，旋轉矩陣M中的 9 個元素均可由這 3 個引數計算出，因此我們通過構建幾個 2D 旋轉變換來描述 3D旋轉。

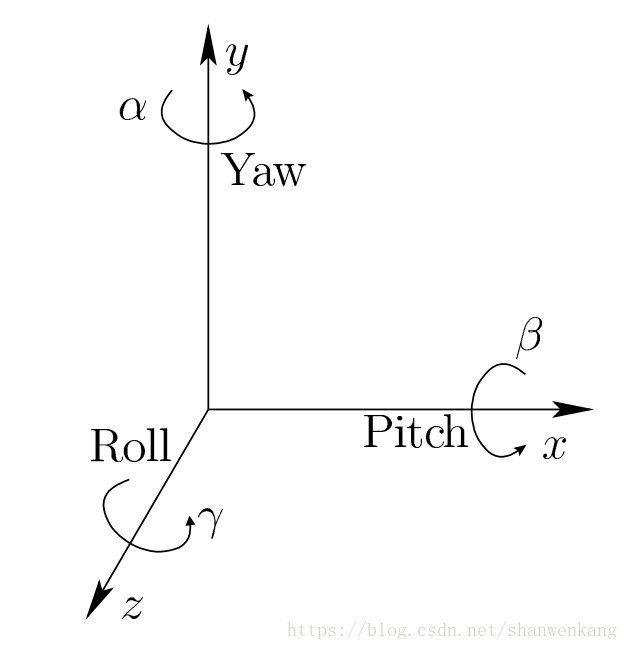
用翻滾角（roll） 來表示繞 z 軸逆時針方向的旋轉γ，用俯仰角（pitch） 來表示繞 x 軸的逆時針旋轉β，用偏航角（yaw） 來表示繞 y 軸的逆時針旋轉α，旋轉矩陣如下：

偏航角、俯仰角、翻滾角經過組合可以表示所有可能的 3D 旋轉：

需要注意的是矩陣乘法是“後向的”，也就是說對一個向量p進行旋轉的時候是將它左乘矩陣，因此旋轉RQp是先用Q進行旋轉，然後再用R進行旋轉。還需要注意的是上式中的順序不可顛倒，因為它不滿足交換律。例如，先旋轉π/2 的偏航角，再旋轉π/2 的俯仰角與先旋轉俯仰角再旋轉偏航角的結果是不一樣的。

平移+旋轉

我們用一個旋轉矩陣 R 進行旋轉，緊接著平移（xt， yt， zt），代數形式如下所示：

如果可以通過一次操作同時完成平移和旋轉，那我們使用起來將會方便很多。儘管我們沒有辦法通過一個 3x3 的矩陣完成如上操作，但是我們可以增加矩陣的維度，用一個 4×4 的齊次變換矩陣來表示。

符號Trb指代一個做剛體變換的矩陣，也就是說，不包含扭曲變形。一個齊次變換矩陣可能包含其他種類的變換。因此一個原始點經過平移加旋轉可以表示為

我們經常會想要進行反變換，對於平移變換（xt， yt， zt），只需簡單地對其取相反數（‐xt， ‐yt， ‐zt）即可；對於一般的矩陣變換 M，我們取它的逆 M‐1（如果存在）。這計算起來通常很複雜，但幸運的是，對於我們所研究的情況，它們的逆計算起來要簡單很多。對於旋轉矩陣 R， 取逆的過程相當於取它的轉置 R‐1=RT。 對於上述， 它的反變換寫為：

經過上述過程就可以將矩陣的平移與旋轉用一個4×4的矩陣表示了