十七 樹結構,二分搜尋樹
為什麼要研究樹結構?
樹結構並不抽象,例如家譜,資料夾等等
優點: 高效

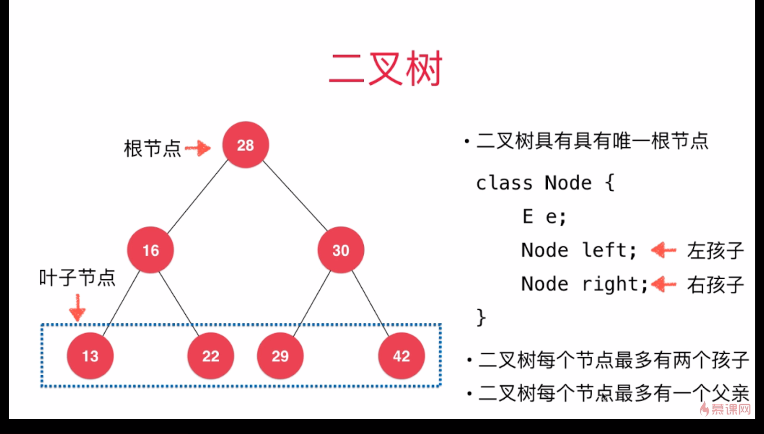
何為二叉樹?
- 和連結串列一樣,是動態資料結構,是天然遞迴結構(每個結點的左子樹也是二叉樹),但是是非線性的
- 二叉樹具有唯一根節點,每個結點最多隻能分兩個叉,每個結點最多有兩個孩子,每個結點最多有一個父親
- 一個孩子都沒有的結點稱為葉子結點
- 二叉樹不一定是滿的,一個結點也是二叉樹,空也是
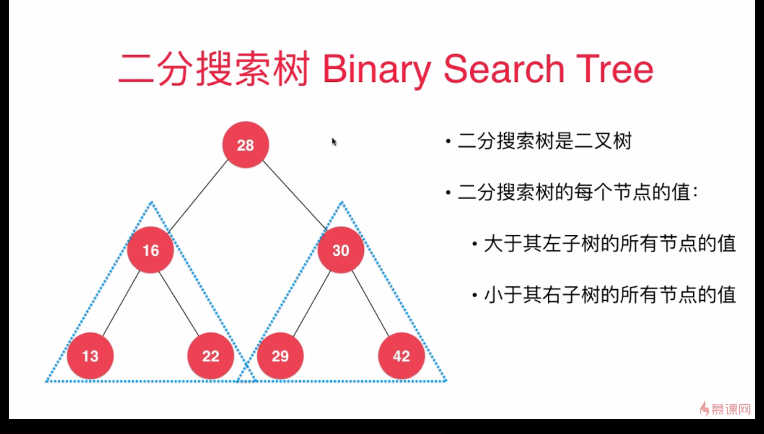
二叉搜尋樹:
儲存的元素必須有可比較性;如果儲存學生,可以按照學號等進行比較。
相關推薦
十七 樹結構,二分搜尋樹
為什麼要研究樹結構? 樹結構並不抽象,例如家譜,資料夾等等 優點: 高效 何為二叉樹? 和連結串列一樣,是動態資料結構,是天然遞迴結構(每個結點的左子樹也是二叉樹),但是是非線性的 二叉樹具有唯一根節點,每個結點最多隻能分兩個叉,每個結點最多有兩個孩子,每
玩轉資料結構(08)--二分搜尋樹
二分搜尋樹(Binary Search Tree) 一、樹結構 使用樹結構的原因: 1.樹結構是一種天然的組織結構 2.資料使用樹結構儲存後,查詢高效 二叉樹:是動態資料結構【不需要在建立資料結構的時候就決定好要儲存多少資料,要新增元
資料結構-使用二分搜尋樹實現集合(Set)
概述 集合不能新增重複元素 可以使用二分搜尋樹很方便的實現集合 集合的典型應用 : 客戶統計 詞彙量統計 程式碼實現 集合可以很方便的使用二分搜尋樹進行實現, 現在引用上面實現的二分搜尋樹實現集
資料結構學習——二分搜尋樹(1)
二分搜尋樹(Binary search tree):滿足任何節點的鍵值大於等於該節點左子樹中的所有鍵值,小於等於該節點右子樹中的所有鍵值的樹。(如下圖) (使用Java實現二分搜尋樹,由於該資料結構的特點所以要求存入的元素必須可以比較,這裡通過繼承
資料結構與演算法C++之二分搜尋樹的刪除節點,刪除任意節點
上篇部落格介紹了怎樣刪除二分搜尋樹的最大值和最小值節點,下面介紹怎樣刪除樹的任意一個節點 上篇刪除最大值節點的操作,其實刪除的節點要麼沒有左右子節點,要麼只可能有左節點, 同樣,刪除最小值節點的操作,其實刪除的節點要麼沒有左右子節點,要麼只可能有右節點 (1)刪
資料結構---二分搜尋樹(java實現)
樹 樹的分類 1、 二分搜尋樹 2、 平衡二叉樹: AVL;紅黑樹 3、 堆; 並查集 4、線段樹;Trie(字典樹、字首樹) 二叉樹 二叉樹具有天然的遞迴結構 每個節點的左子樹也是二叉樹 每個節點的右子樹也是二叉樹 二叉樹不一定是“滿”的 一
十八 二分搜尋樹的三種遍歷方式
三種遍歷方式: package com.lt.datastructure.BST; public class BST<E extends Comparable<E>> { private class Node{ public E e;
十九 二分搜尋樹的廣度優先遍歷
二分搜尋樹廣度優先遍歷的實現: /* * 二分搜尋樹的層序遍歷(廣度優先遍歷),佇列實現 * 廣度優先遍歷優勢在於更快找到想要查詢的元素,主要用於搜尋策略,演算法設計--最短路徑(無權圖) */ public void levelOrder(){
看得見的資料結構Android版之二分搜尋樹結構的實現
零、前言 1.個人感覺這個二叉搜尋樹實現的還是很不錯的,基本操作都涵蓋了 2.在Activity中對view設定監聽函式,可以動態傳入資料,只要可比較,都可以生成二分搜尋樹 3.二分搜尋樹的價值:搜尋、新增、刪除、更新速度快,最佳狀態複雜度logn,但極端情況下會退化成單鏈表 4.本例操作演示原始碼:
資料結構實現 4.1:集合_基於二分搜尋樹實現(C++版)
資料結構實現 4.1:集合_基於二分搜尋樹實現(C++版) 1. 概念及基本框架 2. 基本操作程式實現 2.1 增加操作 2.2 刪除操作 2.3 查詢操作 2.4 其他操作 3. 演算法複雜度分析
資料結構實現 3.1:二分搜尋樹(C++版)
資料結構實現 3.1:二分搜尋樹(C++版) 1. 概念及基本框架 2. 基本操作程式實現 2.1 增加操作 2.2 刪除操作 2.3 查詢操作 2.4 遍歷操作 2.5 其他操作 3. 演算法複雜度分
資料結構——樹結構【二叉樹與二分搜尋樹】
關於樹的一些概念 節點的度 結點擁有的子樹數稱為結點的度。度為0的結點稱為葉子結點或終端結點,度不為0的結點稱為非終端結點或分支結點。除根結點以外,分支結點也稱為內部結點。樹的度是樹內各結點的度的最大值。 層次與深度 有序與無序樹 樹林
資料結構-二分搜尋樹(Binary Search Tree)
特點 動態資料結構 是一顆二叉樹 二分搜尋樹的每個節點的值: 每個節點的值都大於其左子樹的所有節點的值 每個節點的值都小於其右子樹的所有節點的值 每一顆子樹也是二分搜尋樹 儲存的元素必須有可比較性, Java中的話就要求二分搜尋樹儲存
Python-資料結構與演算法(九、二分搜尋樹)
保證一週更兩篇吧,以此來督促自己好好的學習!程式碼的很多地方我都給予了詳細的解釋,幫助理解。好了,幹就完了~加油! 宣告:本python資料結構與演算法是imooc上liuyubobobo老師java資料結構的python改寫,並添加了一些自己的理解和新的東西
資料結構與演算法C++之二分搜尋樹的順序性
二分搜尋樹可以查詢最小值 minimum 和最大值 maximum 可以找到一個元素的前驅(successor),後繼(predecessor),floor,和 ceil 當該元素在樹中時,前驅後繼和f
玩轉資料結構——第五章:二分搜尋樹
內容概要: 為什麼要研究樹結構 二分搜尋樹基礎 向二分搜尋樹中新增元素 改進新增操作:深入理解遞迴終止條件 二分搜尋樹的查詢操作 二手搜尋樹的前序遍歷 二分搜尋樹的中序遍歷和後序遍歷 深入理解二分搜尋樹的前中後遍歷(深度遍歷) 二分搜尋樹是的
查詢演算法(二叉搜尋樹查詢,二分查詢,hash查詢)
這個是在連結串列基礎上根據實驗內容然後添加了一個二分查詢的功能: 二分查詢在競賽極其開發中極其有用,尤其是二分的思想!!! [cpp] view plain copy print? usi
初學資料結構--二分搜尋樹
開發十年,就只剩下這套架構體系了! >>>
淺析二分搜尋樹的資料結構的實現(Java 實現)
[toc] # 樹結構簡介 - 線上性資料結構中,資料都是排成一排存放的;而樹結構則是非線性的,儲存在其中的資料是按分支關係組織起來的結構,就像自然界中的樹那樣。如下圖所示: 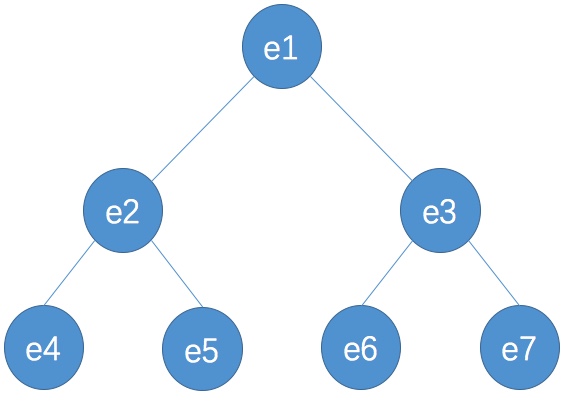 -
數據結構,字典序樹
csdn body 打開鏈接 鏈接 分享 blog -m con pos 點擊打開鏈接,好博客分享下
