資料結構實現 3.1:二分搜尋樹(C++版)
資料結構實現 3.1:二分搜尋樹(C++版)
1. 概念及基本框架
二分搜尋樹 是一種 半線性結構 ,而且儲存上屬於 鏈式儲存(即記憶體的物理空間是不連續的),是樹形結構的一種。二分搜尋樹結構如下圖所示:
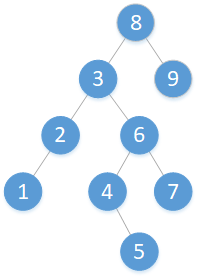
首先,二分搜尋樹 作為 二叉樹 的一種,有著二叉樹的基本特性:
1.每個結點( 根結點 除外)都有一個 前驅結點(即其父結點)。
2.每個結點至多有兩個 後繼結點(即其子結點)。
此外,二分搜尋樹還有一些特殊的特性:
1.每個結點 左孩子 及其後代的值都 小於 這個結點的值。
2.每個結點 右孩子 及其後代的值都 大於 這個結點的值。
3.結點的值 不重複 。
所以,能以二分搜尋樹結構存放的資料有著一條基本要:可比性 。
下面以一個我實現的一個簡單的二分搜尋樹類來進一步理解二分搜尋樹。
template <class T>
class BTNode{
public:
BTNode 和連結串列類似,首先設計一個 結點類 ,這個結點類包含 資料 和 指向左右兩邊結點的指標 。結點類的建構函式可以直接對結點賦值,然後利用結點類物件來建立一棵二叉搜尋樹。二叉搜尋樹類的設計如下:
template <class T>
class BST{
public:
BST(){
root = NULL;
}
...
private:
BTNode<T> *root;
int m_size;
};
這裡為了避免重複設計就可以相容更多資料型別,引入了 泛型 ,即 模板 的概念。(模板的關鍵字是 class 或 typename)
這裡的 root 表示 根節點 ,m_size 表示 二分搜尋樹大小 。為了保護資料,這些變數都設定為 private 。
與連結串列不同的是,二分搜尋樹一般不需要引入 虛擬頭結點 的概念。
實現了前面的程式之後,接下來就是一個二分搜尋樹的增、刪、查以及一些其他基本操作,接下來利用程式碼去實現。
2. 基本操作程式實現
2.1 增加操作
template <class T>
class BST{
public:
...
//增加操作
void add(T num);
...
private:
BTNode<T>* add(BTNode<T> *node, T num);
...
};
首先,在類體內進行增加操作函式的原型說明。這裡包括兩個函式:
add (public)
add (private)
這裡為什麼這麼做呢?因為對於樹結構來講,不管是增、刪、改、查,還是遍歷操作,根節點是一個很重要的結點。為了保護資料,這個結點一般對使用者是遮蔽的,即使用者不需要知道根節點就可以完成需要的操作。
而對於樹結構來說,這些操作一般都是通過遞迴來實現的(某些操作使用了非遞迴的方式進行了實現),遞迴的時候往往需要結點引數,所以這裡利用了一個 public 函式來呼叫另一個 private 函式實現操作,下面的操作也是這樣。
注:樹的操作也可以使用非遞迴的方式實現,這裡只是為了方便程式碼編寫以及理解,使用了遞迴的方式。同理,對於連結串列的操作而言,也可以使用遞迴的方式進行實現。
template <class T>
void BST<T>::add(T num){
root = add(root, num);
}
template <class T>
BTNode<T>* BST<T>::add(BTNode<T> *node, T num){
if (node == NULL){
m_size++;
return new BTNode<T>(num);
}
else if (num < node->m_data){
node->left = add(node->left, num);
}
else if(num > node->m_data){
node->right = add(node->right, num);
}
return node;
}
由於這些函式在類體外,所以每個函式頭部必須新增一行程式碼:
template <class T>
表示該函式使用模板,下面同理。
注意理解這裡私有的 add 函式,為了方便程式碼編寫,特意加了返回值。如果不加返回值,函式是通過父結點連線要新增的子結點,而加了返回值就可以將子結點返回給父結點,操作更加簡便。
2.2 刪除操作
對於二分搜尋樹來說,為了保證刪除操作完成後的樹依舊是一棵二分搜尋樹,我們需要分三種情況討論:
(1)欲刪除結點左右子樹均為空
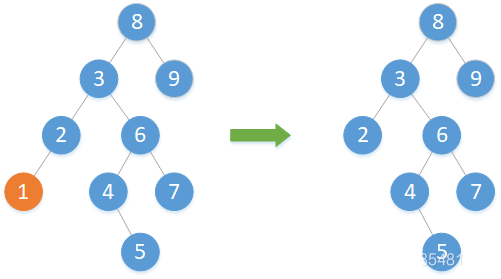
若左右子樹均為空,則直接刪除該結點,並將其父結點指向刪除結點的指標清空。
(2)欲刪除結點左右子樹僅一方為空
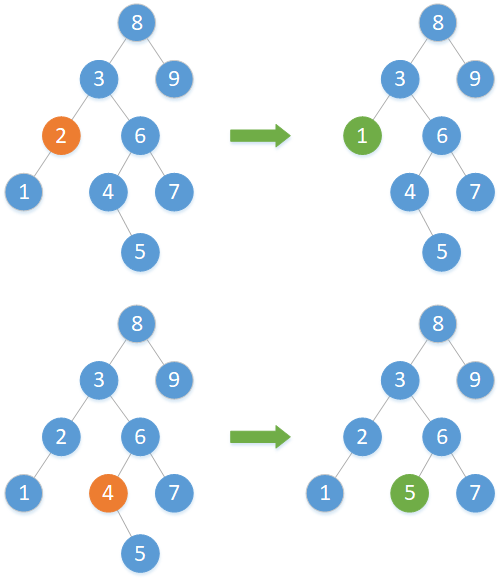
若左右子樹僅一方為空,則刪除該結點,並將該結點不為空的子樹連線到刪除結點的父結點指向刪除結點的那一支。
(3)欲刪除結點左右子樹均不為空
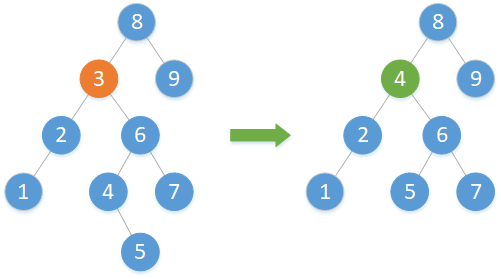
若左右子樹均不為空,就用刪除結點的右邊第一個結點的最左邊的結點(即一直往左走,直到該結點的左子樹為空的那個結點)來替換掉刪除結點,然後刪除掉該結點。而用來替換的那個結點的後代也注意需要維護,不能丟失。
template <class T>
class BST{
public:
...
//刪除操作
void remove(T num);
...
private:
...
BTNode<T>* remove(BTNode<T> *node, T num);
...
};
同理,在類體內進行刪除函式的原型說明。這裡包括兩個函式:
remove (public)
remove (private)
分別去實現它們。
template <class T>
void BST<T>::remove(T num){
root = remove(root, num);
}
template <class T>
BTNode<T>* BST<T>::remove(BTNode<T> *node, T num){
if (node == NULL){
return node;
}
if (num < node->m_data){
node->left = remove(node->left, num);
}
else if (num > node->m_data){
node->right = remove(node->right, num);
}
else if (num == node->m_data){
if (node->left == NULL){
BTNode<T> *rightNode = node->right;
delete node;
m_size--;
return rightNode;
}
else if (node->right == NULL){
BTNode<T> *leftNode = node->left;
delete node;
m_size--;
return leftNode;
}
else{
BTNode<T> *minNode = node->right;
for (; minNode->left; minNode = minNode->left);
node->m_data = minNode->m_data;
node->right = remove(node->right, minNode->m_data);
return node;
}
}
return node;
}
2.3 查詢操作
template <class T>
class BST{
public:
...
//查詢操作
bool contains(T num);
...
private:
...
bool contains(BTNode<T> *node, T num);
...
};
同樣,查詢操作也有兩個函式:
contains (public)
contains (private)
template <class T>
bool BST<T>::contains(T num){
return contains(root, num);
}
template <class T>
bool BST<T>::contains(BTNode<T> *node, T num){
if (node == NULL){
return false;
}
if (num == node->m_data){
return true;
}
else if (num < node->m_data){
return contains(node->left, num);
}
else{
return contains(node->right, num);
}
}
2.4 遍歷操作
樹的遍歷是一個很重要的概念,下面給出一張圖來說明四種遍歷的過程。
注:因為二叉樹的遍歷操作是通用的,所以這裡並沒有以二分搜尋樹為例子,而是一棵普通的二叉樹。
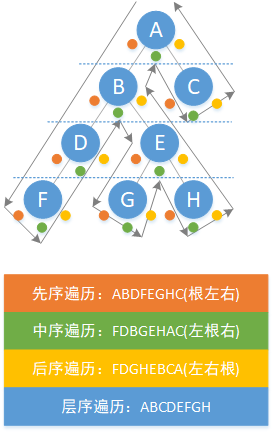
二叉樹的先(中或後)序遍歷實際上表示的是結點被訪問第幾次會輸出。
先序遍歷表示第一次被訪問時(橙色)會輸出;
中序遍歷表示第二次被訪問時(綠色)會輸出;
後序遍歷表示第三次被訪問時(黃色)會輸出。
這三種遍歷的遞迴版本比較容易實現,依靠輸出位置的不同決定是哪一種遍歷。這三種遍歷實質上是一種 深度優先 遍歷。而非遞迴版本比較難,下面也給出了一種程式實現方法。
注:這三種遍歷的非遞迴版本利用呼叫棧來實現,這裡我們使用了我們在 1.2 中實現的 陣列棧 作為呼叫棧。
層序遍歷表示一層一層(圖中的藍色虛線)的訪問輸出,使用的是非遞迴的方法,呼叫了一個佇列來實現,層序遍歷實質上是一種 廣度優先 遍歷。
注:層序遍歷實現利用了我們在 1.4 中實現的 迴圈佇列 作為呼叫佇列。
template <class T>
class BST{
public:
...
//遍歷操作
void preOrder();
void inOrder();
void postOrder();
void preOrderNR();
void inOrderNR();
void postOrderNR();
void levelOrder();
private:
...
void preOrder(BTNode<T> *node);
void inOrder(BTNode<T> *node);
void postOrder(BTNode<T> *node);
...
};
這裡遍歷函式較多,一共有十個:
preOrder (public):先序遍歷
preOrder (private)
preOrder (public):中序遍歷
preOrder (private)
preOrder (public):後序遍歷
preOrder (private)
preOrderNR:先序遍歷(非遞迴版本)
inOrderNR:中序遍歷(非遞迴版本)
postOrderNR:後序遍歷(非遞迴版本)
levelOrder:層序遍歷
和前面的函式一樣,遞迴版本的遍歷函式有 public 和 private 兩個,實現遞迴版本遍歷的操作。然後又實現了三種遍歷操作的非遞迴版本,以及層序遍歷(非遞迴)。下面分別對它們進行實現。
template <class T>
void BST<T>::preOrder(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "先序遍歷:";
preOrder(root);
cout << endl;
}
template <class T>
void BST<T>::preOrder(BTNode<T> *node){
if (node == NULL){
return;
}
cout << node->m_data << " ";
preOrder(node->left);
preOrder(node->right);
}
template <class T>
void BST<T>::inOrder(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "中序遍歷:";
inOrder(root);
cout << endl;
}
template <class T>
void BST<T>::inOrder(BTNode<T> *node){
if (node == NULL){
return;
}
inOrder(node->left);
cout << node->m_data << " ";
inOrder(node->right);
}
template <class T>
void BST<T>::postOrder(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "後序遍歷:";
postOrder(root);
cout << endl;
}
template <class T>
void BST<T>::postOrder(BTNode<T> *node){
if (node == NULL){
return;
}
postOrder(node->left);
postOrder(node->right);
cout << node->m_data << " ";
}
template <class T>
void BST<T>::preOrderNR(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "先序遍歷(非遞迴):";
ArrayStack<BTNode<T>*> s;
s.push(root);
while (!s.isEmpty()){
BTNode<T> *node = s.peek();
cout << node->m_data << " ";
s.pop();
if (node->right != NULL){
s.push(node->right);
}
if (node->left != NULL){
s.push(node->left);
}
}
cout << endl;
}
template <class T>
void BST<T>::inOrderNR(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "中序遍歷(非遞迴):";
ArrayStack<BTNode<T>*> s;
BTNode<T> *node = root;
while (node != NULL || !s.isEmpty()){
while (node != NULL){
s.push(node);
node = node->left;
}
node = s.peek();
cout << node->m_data << " ";
s.pop();
if (node->right != NULL){
node = node->right;
}
else{
node = NULL;
}
}
cout << endl;
}
template <class T>
void BST<T>::postOrderNR(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "後序遍歷(非遞迴):";
ArrayStack<BTNode<T>*> s;
BTNode<T> *node = root;
BTNode<T> *lastVisited = root;
while (node != NULL || !s.isEmpty()){
while (node != NULL){
s.push(node);
node = node->left;
}
node = s.peek();
if (node->right != NULL && lastVisited != node->right){
node = node->right;
}
else{
lastVisited = node;
cout << node->m_data << " ";
s.pop();
node = NULL;
}
}
cout << endl;
}
template <class T>
void BST<T>::levelOrder(){
cout << "Binary Search Tree: " << "Size = " << m_size << endl;
cout << "層序遍歷:";
LoopQueue<BTNode<T>*> q;
q.enqueue(root);
while (!q.isEmpty()){
BTNode<T> *node = q.front();
cout << node->m_data << " ";
q.dequeue();
if (node->left != NULL){
q.enqueue(node->left);
}
if (node->right != NULL){
q.enqueue(node->right);
}
}
cout << endl;
}
2.5 其他操作
二分搜尋樹還有一些其他的操作,這些函式我在類體內進行了實現。
包括 二分搜尋樹大小 的查詢等操作。
template <class T>
class BST{
public:
...
int size(){
return m_size;
}
bool isEmpty(){
return root == NULL;
}
...
};
3. 演算法複雜度分析
3.1 增加操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| add | O(n) | O(logn) |
因為二分搜尋樹的特有性質,這裡平均複雜度是以 2 為底 n 的對數,簡單寫作 logn ,即其是對數級別的時間複雜度,下面的同理,這正是二分搜尋樹的優點。
3.2 刪除操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| remove | O(n) | O(logn) |
3.3 查詢操作
| 函式 | 最壞複雜度 | 平均複雜度 |
|---|---|---|
| contains | O(n) | O(logn) |
總體情況:
| 操作 | 時間複雜度 |
|---|---|
| 增 | O(logn) |
| 刪 | O(logn) |
| 查 | O(logn) |
因為二分搜尋樹的特有性質,所以操作的複雜度都是 O(logn) 級別的,和線性結構相比,(線性結構很多操作需要 O(n) 級別的時間複雜度)充分體現出二分搜尋樹這一結構的優點。
4. 完整程式碼
程式完整程式碼(這裡使用了標頭檔案的形式來實現類)如下:
其中,陣列棧 類以及 迴圈佇列 類的程式碼不再重複給出,如有需要,可以檢視 1.2 和 1.4的內容。
#ifndef __BST_H__
#define __BST_H__
#include "ArrayStack.h"
#include "LoopQueue.h"
template <class T>
class BTNode{
public:
BTNode(T num, BTNode<T> *left = NULL, BTNode<T> *right = NULL){
m_data = num;
this->left = left;
this->right = right;
}
public:
T m_data;
BTNode<T> *left;
BTNode<T> *right;
相關推薦
資料結構實現 3.1:二分搜尋樹(C++版)
資料結構實現 3.1:二分搜尋樹(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 增加操作
2.2 刪除操作
2.3 查詢操作
2.4 遍歷操作
2.5 其他操作
3. 演算法複雜度分
玩轉資料結構——第五章:二分搜尋樹
內容概要:
為什麼要研究樹結構
二分搜尋樹基礎
向二分搜尋樹中新增元素
改進新增操作:深入理解遞迴終止條件
二分搜尋樹的查詢操作
二手搜尋樹的前序遍歷
二分搜尋樹的中序遍歷和後序遍歷
深入理解二分搜尋樹的前中後遍歷(深度遍歷)
二分搜尋樹是的
資料結構實現 4.1:集合_基於二分搜尋樹實現(C++版)
資料結構實現 4.1:集合_基於二分搜尋樹實現(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 增加操作
2.2 刪除操作
2.3 查詢操作
2.4 其他操作
3. 演算法複雜度分析
資料結構實現 5.1:對映_基於樹實現(C++版)
資料結構實現 5.1:對映_基於樹實現(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 增加操作
2.2 刪除操作
2.3 修改操作
2.4 查詢操作
2.5 其他操作
3. 演算法複
資料結構實現 9.1:並查集_陣列結構實現(C++版)
資料結構實現 9.1:並查集_陣列結構實現(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 聯合操作
2.2 查詢操作
2.3 其他操作
3. 演算法複雜度分析
3.1 聯合操作
資料結構實現 8.1:字典樹(C++版)
資料結構實現 8.1:字典樹(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 增加操作
2.2 查詢操作
2.3 其他操作
3. 演算法複雜度分析
3.1 增加操作
3.2 查
資料結構實現 6.1:二叉堆_基於動態陣列實現(C++版)
資料結構實現 6.1:二叉堆_基於動態陣列實現(C++版)
1. 概念及基本框架
1.1 滿二叉樹
1.2 完全二叉樹
2. 基本操作程式實現
2.1 增加操作
2.2 刪除操作
2.3 查詢操作
資料結構實現 10.1:AVL樹(C++版)
資料結構實現 10.1:AVL樹(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 增加操作
2.1.1 左左
2.1.2 右右
2.1.3 左右
2.1.4 右左
2.1
資料結構實現 2.1:連結串列(C++版)
1. 概念及基本框架
連結串列 是一種 線性結構 ,而且儲存上屬於 鏈式儲存(即記憶體的物理空間是不連續的),是線性表的一種。連結串列結構如下圖所示:
下面以一個我實現的一個簡單的連結串列類來進一步理解連結串列。
template <class T&g
資料結構實現(六):連結串列棧(C++版)
資料結構實現(六):連結串列棧(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 入棧操作
2.2 出棧操作
2.3 查詢操作
2.4 其他操作
3. 演算法複雜度分析
3.1
浙大版《資料結構》習題4.3 是否二叉搜尋樹 (25 分)
本題要求實現函式,判斷給定二叉樹是否二叉搜尋樹。
函式介面定義:
bool IsBST ( BinTree T );
其中BinTree結構定義如下:
typedef struct TNode *Position;
typedef Position BinT
自定義樹(2):二分搜尋樹(Binary Search Tree)
二分搜尋樹也是一種二叉樹。
二分搜尋樹的遍歷:
層序遍歷圖解:
刪除任意元素圖解:
程式碼實現:
packa
openjudge資料結構練習集 1:集合的交運算(單鏈表)
集合的交運算(單鏈表)總時間限制: 1000ms記憶體限制: 65536kb描述利用兩個單鏈表LA和LB分別表示兩個集合A和B(即線性表中的資料元素即為集合中的成員),要求一個新的集合A=A∩B。這就要求對連結串列作如下操作:將存在於表LA中,同時又存在於LB中的資料元素保留
c語言資料結構實現-雜湊表/雜湊桶(hashtable/hashbucket)
一、需求
以“key-value”的形式進行插入、查詢、刪除,是否可以考慮犧牲空間換時間的做法?
二、相關知識
雜湊表(Hashtable)又稱為“雜湊表”,Hashtable是會根據索引鍵的雜湊程式程式碼組織成的索引鍵(Key)和值(Value)配對的集合。Hashtab
演算法3-2:行編輯程式 (c語言)
: 演算法3-2:行編輯程式
時間限制:1 Seconds 記憶體限制:32 Mbyte 總提交:65 正確:9 作者:外部匯入 [提交] [統計] [提問]
題目描述
一個簡單的行編輯程式的功能是:接收使用者從終端輸入的程式或資料,並存入使用者的資料區。由於使用者在終端上進
資料結構之單鏈表的增刪改查(java版)
talk is cheap,show you zhe code;
/*
* 單鏈表的遍歷是從第0個節點開始 沿著next鏈,一次訪問每個節點並且每個節點只能訪問一次
* 當頭結點head為空時 此連結串列為空連結串列
*
* 插入操作
* 1空
二叉搜尋樹(C語言)
二叉搜尋樹又稱二叉排序樹,他或者是一顆空樹,或者是具有以下性質的二叉樹
1、若它的左子樹不為空,左子樹上所有節點的值都小於根節點上的值
2、若它的右子樹不為空,右子樹上所有節點的值都大於根節點上的值
它的左右子樹分別為二叉搜尋樹
用搜索關鍵字的方法先定義
通過不斷的插入生成一棵二叉搜尋樹(C語言)
二叉搜尋樹:其各個節點的關鍵字碼必須是唯一的;若某結點左子樹非空,則左子樹上的所有節點的值均小於該結點的關鍵字碼,而其右子樹上的所有節點的值均大於該結點的關鍵字碼。所以,按照中序周遊整個二叉樹的可以得到一個由小到大的有序排列。通過不斷讀取陣列中的資料而插入生成的二叉搜尋樹的程
資料結構---二分搜尋樹(java實現)
樹
樹的分類
1、 二分搜尋樹
2、 平衡二叉樹: AVL;紅黑樹
3、 堆; 並查集
4、線段樹;Trie(字典樹、字首樹)
二叉樹
二叉樹具有天然的遞迴結構
每個節點的左子樹也是二叉樹
每個節點的右子樹也是二叉樹
二叉樹不一定是“滿”的
一
資料結構實現 6.3:優先佇列_基於動態陣列實現(C++版)
資料結構實現 6.3:優先佇列_基於動態陣列實現(C++版)
1. 概念及基本框架
2. 基本操作程式實現
2.1 入隊操作
2.2 出隊操作
2.3 查詢操作
2.4 其他操作
3. 演算法複雜度分析
