TDOA is the difference in arrival times of the emitted signal received at a pair of sensors, implying that clock synchronization across all receivers is required. Nevertheless, the TDOA scheme is simpler than the TOA method because the latter needs the source to be synchronized as well, which implies a higher hardware cost. Similar to the TOA, multiplying the TDOA by the known propagation speed leads to the range difference between the source and two receivers. 

As discussed in blog：Time - Difference - of - Arrival ( TDOA ) Estimation Preliminary introduction , geometrically, each noise - free TDOA defines a hyperbola on which the source must lie in the 2 - D space, and the target location is given by the intersection of at least two hyperbolae. In the presence of disturbance, we estimate x from a set of hyperbolic equations converted from the TDOA measurements.

Mathematically, the TDOA measurement model is formulated as follows. We assume that the source emits a signal at the unknown time   and the l th sensor receives it at time with L ≥ 3. There are L ( L − 1)/2 distinct TDOAs from all possible sensor pairs, denoted by   with k > l . However, there are only ( L − 1) nonredundant TDOAs. Taking L = 3 as an example, the distinct TDOAs are

, and we easily observe that , which is redundant. In order to reduce complexity without sacrificing estimation performance, we should measure all L ( L − 1)/2 TDOAs and convert them to ( L − 1) nonredundant TDOAs for source localization [11] . Without loss of generality, we consider the fi rst sensor as the reference and the nonredundant TDOAs are .

Thus, the range difference measurements deduced from the TDOAs are modeled as

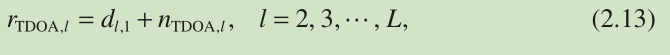
where

and is the range difference error in , which is proportional to the disturbance in . Following the TOA , the TDOA signal model in matrix form is

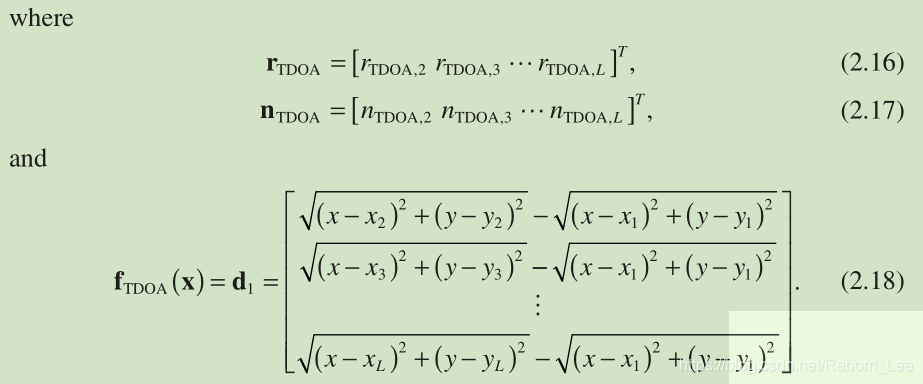
The source localization problem based on TDOA measurements is to estimate x given { } or .
Assuming that is zero - mean and Gaussian distributed, the PDF for , denoted by , is

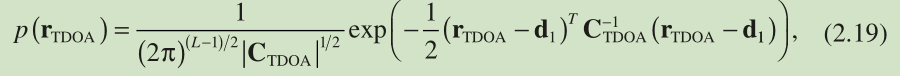
where is the covariance matrix for . Alternatively, we can write  . Since all TDOAs are determined with respect to the first sensor, , are correlated. As a result, is not a diagonal matrix [11] .