目錄

Abstract

Introduction

BLUE-based positioning

 BLUE-LSC algorithm

 BLUE-LLS algorithm

Abstract

 A common technique for source localisation is to utilise the time-of-arrival (TOA) measurements between the source and several spatially separated sensors. The TOA information defines a set of circular equations from which the source position can be calculated with the knowledge of the sensor positions.

源定位的常用技術是利用源和若干空間分離的感測器之間的到達時間（TOA）測量。 TOA資訊定義了一組圓形方程，從中可以利用感測器位置的知識計算源位置。
Apart from nonlinear optimisation, least squares calibration (LSC) and linear least squares (LLS) are two computationally simple positioning alternatives which reorganise the circular equations into a unique and non-unique set of linear equations, respectively. As the LSC and LLS algorithms employ standard least squares (LS), an obvious improvement is to utilise weighted LS estimation.

除了非線性優化之外，最小二乘校準（LSC）和線性最小二乘（LLS）是兩種計算上簡單的定位選擇，它們將圓形方程分別重新組織成一組唯一且非唯一的線性方程組。 由於LSC和LLS演算法採用標準最小二乘（LS），因此明顯的改進是利用加權LS估計。

In the paper, it is proved that the best linear unbiased estimator (BLUE) version of the LLS algorithm will give identical estimation performance as long as the linear equations correspond to the independent set. The equivalence of the BLUE-LLS approach and the BLUE variant of the LSC method is analysed. Simulation results are also included to show the comparative performance of the BLUE-LSC, BLUE-LLS, LSC, LLS and constrained weighted LSC methods with Crame´r–Rao lower bound.

在本文中，證明了LLS演算法的最佳線性無偏估計（BLUE）版本將給出相同的估計效能，只要線性方程對應於獨立集合。 分析了BLUE-LLS方法與LSC方法的BLUE變體的等價性。 還包括模擬結果，以顯示BLUE-LSC，BLUE-LLS，LSC，LLS和具有Crame'r-Rao下限的約束加權LSC方法的比較效能。

注：最佳線性無偏估計(best linear unbiased estimator)（BLUE）

Introduction

Source localisation using measurements from an array of spatially separated sensors has been an important problem in radar, sonar, global positioning system [1], mobile communications [2], multimedia [3] and wireless sensor networks [4]. One commonly used location-bearing parameter is the time-of-arrival (TOA) [2, 4], that is, the one-way signal propagation or round trip time between the source and sensor. For two-dimensional positioning, each noise-free TOA provides a circle centred at the sensor on which the source must lie. By using M >= 3 sensors, the source location can be uniquely determined by the intersection of circles. In practice, the TOA measurements
are noisy, which implies multiple intersection points and thus they are usually converted into a set of circular equations, from which the source position is estimated with the knowledge of the signal propagation speed and sensor array geometry.

Commonly used techniques for solving the circular equations include linearisation via Taylor-series expansion [5] and steepest descent method [6]. Although this direct approach can attain optimum estimation performance, it is computationally intensive and sufficiently precise initial estimates are required to obtain the global solution. On the other hand, an alternative approach, which allows real-time
computation and ensures global convergence is to reorganise the nonlinear equations into a set of linear equations by introducing an extra variable that is a function of the source position. It is noteworthy that this idea is first introduced in [7, 8] for time-difference-of-arrival (TDOA) based localisation.

解決圓形方程的常用技術包括通過泰勒級數展開[5]和最速下降法[6]的線性化。 儘管這種直接方法可以獲得最佳估計效能，但它是計算密集型的，並且需要足夠精確的初始估計來獲得全域性解。 另一方面，允許實時計算並確保全域性收斂的替代方法是通過引入作為源位置的函式的額外變數將非線性方程組織成一組線性方程。 值得注意的是，這個想法首先在[7,8]中引入，用於基於時間差（TDOA）的定位。

The linear equations can then be solved straightforwardly by using least squares (LS) and the corresponding estimator is referred to as the least squares calibration (LSC) method [9], or by eliminating the common variable via subtraction of each equation from all others, which is referred to as the linear least squares (LLS) estimator [10, 11].

然後可以通過使用最小二乘（LS）直接求解線性方程，並且相應的估計器被稱為最小二乘校準（LSC）方法[9]，或者通過從所有其他方程中減去每個方程來消除公共變數， 這被稱為線性最小二乘（LLS）估計[10,11]。

 In this work, we will focus on the relationship development between the best linear unbiased estimator (BLUE) [12] versions of the LSC and LLS algorithms. Our contributions do not lie on new positioning algorithm development as the BLUE technique for localisation applications has already been proposed in the literature [13]. Our major findings include

在這項工作中，我們將重點關注LSC和LLS演算法的最佳線性無偏估計（BLUE）[12]版本之間的關係開發。 我們的貢獻不在於新的定位演算法開發，因為文獻中已經提出了用於定位應用的BLUE技術[13]。 我們的主要發現包括

(i) all BLUE realisations of the LLS algorithm have identical estimation performance as long as the (M -1) linear equations correspond to the independent set [10].

（i）所述LLS演算法的所有實現中BLUE具有相同的估計效能，只要該（M-1）的線性方程組對應於獨立組[10]。

(ii) The covariance matrices of the position estimates in the BLUE-LLS scheme with the independent set and the BLUE version of the LSC algorithm are identical.

（ii）BLUE-LLS方案中具有獨立集合的位置估計的協方差矩陣和LSC演算法的藍BLUE版本是相同的。

By comparing with Crame ´r–Rao lower bound (CRLB) for TOA-based localisation [14], it is then shown that they are suboptimal estimators, and this result is different from the iterative BLUE estimator of [13], which gives maximum likelihood estimation performance.

通過與基於TOA的定位的Crame'r-Rao下界（CRLB）進行比較[14]，然後表明它們是次優估計，並且該結果與[13]的迭代BLUE估計不同，其給出最大似然估計效能。

(iii) Among the BLUE-LLS and BLUE-LSC algorithms, the latter is preferable as it involves lower computational complexity. Note that the research results can also be applied to source localisation systems with received signal strength [2] measurements as they employ the same trilateration concept where the propagation path losses from the source to the sensors are measured to give their distances.

（iii）在BLUE-LLS和BLUE-LSC演算法中，後者是優選的，因為它涉及較低的計算複雜度。 請注意，研究結果也可以應用於具有接收訊號強度[2]測量的源定位系統，因為它們採用相同的三邊測量概念，其中測量從源到感測器的傳播路徑損耗以給出它們的距離。

BLUE-based positioning

In this Section, we first present the signal model for TOA-based localisation. The BLUE-LSC and BLUE-LLS algorithms are then devised from the LSC and LLS formulations, respectively. Their relationship, estimation performance and computational complexity are also provided.
Let (x,y) and , i =1, 2, ... , M, be the unknown source position and the known coordinates of the ith sensor, respectively. With known signal propagation speed, the range measurements between the source and sensors are straightforwardly determined from the corresponding TOA measurements, which are modelled as

  is the noise-free range and n i is the noise in r i . For simplicity, we assume line-of-sight propagation between the source and all sensors such that each n i is a zero-mean white process with known variance  [14].

 BLUE-LSC algorithm

BLUE [12] is a linear estimator which is unbiased and has minimum variance among all other linear estimators. To employ the BLUE technique, we need to restrict the parameters to be estimated linear in the data. It is suitable for practical implementation as only the mean and covariance of the data are required and complete knowledge of the probability density function is not necessary. The BLUE
version of the LSC estimator is derived as follows.

Squaring both sides of (1), we have [9]

where  and   is the introduced variable to reorganise (1) into a set of linear equations in x, y and R. To facilitate the development, we express (2) in matrix form

where

and

For sufficiently small noise conditions,  and 

where T denotes transpose operation and E is the expectation operator. Hence we have , which corresponds to the linear unbiased data model. Using the information that p is approximately zero-mean and its covariance matrix, denoted by , is a diagonal matrix of the form

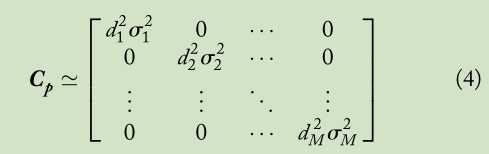
The BLUE for based on (3), denoted by , is then [12]

注： 我信了你的邪，這個[12]參考的是統計訊號處理基礎中的估計理論。我還沒有去檢視這本書的具體解釋，看了幾篇論文都是直接給出。我且先認為就是如此吧！

where -1 represents matrix inverse. Note that the LSC estimate is given by (5) with the substitution of  where is the M * M identity matrix, without utilising the mean and covariance of the data. Since  are unknown, they will be substituted by in practice. The covariance matrix for , denoted by , is [12]

 的協方差矩陣，由表示，是[12]

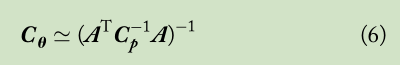
where the variances for the estimates of x and y are given by the (1, 1) and (2, 2) entries of , respectively. It is worthy to mention that the same weighting matrix of  has been proposed in [14], which can be considered as a constrained weighted least squares calibration (CWLSC) algorithm with utilising the constraint of . We expect that the BLUE-LSC algorithm is inferior to the CWLSC scheme as the parameter relationship in is not exploited.

其中x和y估計的方差分別由  的（1,1）和（2,2）條目給出。 值得一提的是，在[14]中提出了相同的加權矩陣，可以將其視為利用約束的約束加權最小二乘校準（CWLSC）演算法。 我們期望BLUE-LSC演算法不如CWLSC方案，因為中的引數關係未被利用。

注：[14]這篇文章的地址為：Least squares algorithms for time-of-arrival-based mobile location

 BLUE-LLS algorithm

On the other hand, subtracting the first equation of (2) from the remaining equations, R can be eliminated and we get
(M - 1) equations

Expressing (7) in matrix form yields

Following the development of the BLUE-LSC algorithm, the BLUE-LLS estimate for  based on (8), denoted by 

where is the covariance matrix for q which has the form of

With the use of matrix inversion lemma, its inverse can be computed as

Note that the LLS estimate is given by (9) with the substitution of ,without utilising the mean and covariance of the data.

The estimator of (9) has minimum variance according to the data model of (8). It is worthy to note that although the dependent variable of R is eliminated in the LLS approach, estimation performance degradation occurs in the conversion of (2) to (7) or (8).

根據（8）的資料模型，（9）的估計量具有最小方差。 值得注意的是，儘管在LLS方法中消除了R的因變數，但在（2）至（7）或（8）的轉換中發生估計效能降級。
This is analogous to TOA and TDOA-based positioning where the former estimation performance bound is lower than that of the latter if the TDOAs are obtained from substraction between the TOAs [15, 16]. The covariance matrix for   denoted by , is

這類似於基於TOA和TDOA的定位，其中如果TDOA是從TOA之間的減法獲得的，則前一估計效能界限低於後者[15,16]。 用於表示的協方差矩陣是

注：這篇文章，看到這裡大致可以了，下面的的確有點生涉難懂，至於模擬暫時就不模擬了。留著以後有閒心了模擬。

其實BLUE_LLS對我還是挺有啟發的，這種啟發在於接下來，我做TDOA定位分析有利。因為這個過程，與TDOA神似，這是後話，後面的博文會作出分析。

Although there are at most M(M - 1) LLS equations can be generated from (2), only (M - 1) are independent [10]. In fact, (7) is an example of the independent set of equations.

雖然最多可以從（2）生成M（M - 1）LLS方程，但只有（M - 1）是獨立的[10]。 實際上，（7）是獨立方程組的一個例子。

Although we can use up to M(M - 1) dependent equations in the standard LLS algorithm, this is not possible for the BLUE realisation because the corresponding noise covariance matrix will be singular. In the following, we will prove that as long as the (M 2 1) equations belong to the independent set, the BLUE-LLS estimator performance will agree with the covariance matrices given by (6) and (12). Their suboptimality is then illustrated by contrasting with the CRLB.

雖然我們可以在標準LLS演算法中使用多達M（M-1）個從屬方程，但這對於BLUE實現是不可能的，因為相應的噪聲協方差矩陣將是單數的。 在下文中，我們將證明只要（M-1）方程屬於獨立集，BLUE-LLS估計器效能將與（6）和（12）給出的協方差矩陣一致。 然後通過與CRLB對比來說明它們的次優性。

First, we define two sets

where corresponds to all independent sets of the LLS equations. In doing so, we can generalise (8) as:

其中  對應於LLS方程的所有獨立集合。 在這樣做時，我們可以將（8）概括為：

As an illustration, substituting in (16) and (17), where is a column vector of length M-1 with all elements equal 1, yield (9) and (12).