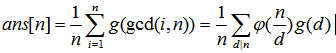You may not know this but it's a fact that Xinghai Square is Asia's largest city square. It is located in Dalian and, of course, a landmark of the city. It's an ideal place for outing any time of the year. And now: 
   
  There are NN children from a nearby primary school flying kites with a teacher. When they have a rest at noon, part of them (maybe none) sit around the circle flower beds. The angle between any two of them relative to the center of the circle is always a multiple of 

Input

There are TT tests (T≤50T≤50). Each test contains one integer NN. 1≤N≤1000000000 (109)1≤N≤1000000000 (109). Process till the end of input.

Output

For each test, output the answer mod 1000000007 (109+7109+7) in one line.

Sample Input

4

7

10

Sample Output

3

5

15

中文題目大意：n個小朋友個一個老師去一個城市廣場放風箏，當n個小朋友停下來休息的時候老師要求他們圍著一個圓形的花壇坐下。不一定每個小朋友都坐下休息，可以都不坐下，但是坐下的兩個小朋友和花壇圓心組成的角必須是2π/n的倍數，但不能等於2π/n。老師想知道，一共有多少種坐下的方法。為了簡化問題，每個小朋友看作是一樣的。為了不讓答案看起來太大，可以通過旋轉變得一樣的方法看作是同一種方法。

題目的數學意義：給定一個圓，和整數n，設圓2πrad平均分成n份後一份的度數為k。n表示欲在圓周上插入小於等於n、大於等於0個點，每兩個點之間的度數是 k的倍數，但不能是k。問：不同的排列種類數。注：每個點都是一樣的，並且是排成一個首尾相接的圓而不是一列或一行，並且滿足旋轉同構。

輸入：

輸入挺大的，考慮用longlong。

輸出：

每一組資料對1e9+7取模，又是排列組合題（涉及乘法除法），考慮用逆元。

樣例輸入輸出：

                   輸入     輸出

第一組：4        3

第二組：7        5

第二組：10       15

解題思路：

首先明確目標，求旋轉同構的環的排列組合種數。

首先想象一下一根圍成圓周的繩子上有n個均勻分佈的點，每兩點間的圓心角弧度是2π/n。每一種情況就是考慮每個點坐不坐人的情況。從任意兩個點中將圍成圓的繩子剪開，這時，規定一下繩子的首尾，繩子便有了第一個點和最後一個點。

從第一個點開始dp考慮每個點取0（不坐人）還是取1（坐人）。因為最後求的是種數，所以令dp[i][0]表示第i個座位如果不坐人計算到i為止，有多少種方法；dp[i][1]表示第i個座位如果坐人，計算到i為止，有多少種方法。顯然dp[1][0]=1,dp[1][1]=1，表示第一個座位坐人，計算到第一個座位為止，有一種方法；同理，第一個座位不坐人也是一種方法。考慮題目條件，第二個點開始，能不能坐人由前一個點決定（前後兩個點是屬於相互影響狀態，所以採用固定前一個點，後一個點作出讓步的辦法，當然也能從後往前算）。

第二個點開始，任意一個點i，如果i-1坐人了，i就不能坐人，如果i-1沒有坐人則i可以坐人或者不坐人。也就是，第i個座位不坐人，對前一個座位沒要求；第i個座位坐人，前一個座位絕對不能坐人。也就是，前一個座位坐人不坐人的方法數都加起來等於後一個座位不坐人的方法數；前一個座位不坐人的方法書等於後一個座位坐人的方法數。則dp[i][0]=dp[i-1][0]+ dp[i-1][1];   dp[i][1]=dp[i-1][0];

i      1       2       3       4       5       6       7       8       9       10     11     12 

dp[i][0]  1        2       3       5       8       13     21     34     55     89     144  233

dp[i][1]     1       1       2       3       5       8       13     21     34     55     89     144

發現是斐波那契數列。

dp到第n個，這個時候考慮把繩子重新首尾相接。顯然，接起來後第一個點和最後一個點會相互影響，但是在剛才的dp中並沒有考慮到。當最後一個點不坐人的時候，算出來有多少種方法就有多少種方法，當最後一個點坐人的時候，第一個點是確定的，一定不能坐人，所以不用考慮，直接從第二個點開始dp，其實還是斐波那契數列，只是算到第n個的時候實際上是第n-1項。所以，連成環後的方法數是num[n]=dp[n-1][1]（最後一個點坐人）+dp[n][0](最後一個點不坐人)，num[n]=dp[n-2][0]+dp[n][0]，結合斐波那契數列，num[n]=fib[n-2+1]+fib[n+1]=fib[n-1]+fib[n+1];

根據fib[n]=bib[n-1]+fib[n-2];

得num[n]=num[n-1]+num[n-2];

通過num[n]=fib[n-1]+fib[n+1];

計算出num[2]=1+2=3;  num[3]=1+3=4

通過num[n]=num[n-1]+num[n-2];  代入  num[2]=3;  num[3]=4

得 num[1]=1

遞推式可以考慮用矩陣快速冪計算。

矩陣快速冪和正常遞推效率比較如下：

接下來的推導涉及離散數學。

現在考慮重構問題。

伯恩賽德引理（Burnside's lemma），設G={a1,a2,…ag}是目標集[1,n]上的置換群。每個置換都寫成不相交迴圈的乘積。  是在置換ak的作用下不動點的個數，也就是長度為1的迴圈的個數。通過上述置換的變換操作後可以相等的元素屬於同一個等價類。若G將[1,n]劃分成l個等價類，則：

等價類個數為：

Poly定理，設是n個物件的一個置換群, 用m種顏色染圖這n個物件，則不同的染色方案數為：

其中，為的迴圈節數

回到題目，考慮旋轉同構，按照一樣的方法（旋轉角度）一次或多次旋轉後相互一致的是一類（在題目中被看作一種），這一類裡面的每一種情況都有一樣長度（和旋轉角度有關）的迴圈節，並且因為旋轉後可以重合所以圍坐著的人數相同，總座位數也相同，所以迴圈節個數相同。但是擁有迴圈節數量、長度一樣的環，不一定是一類環，從離散的角度很容易理解。通俗地講，從“巨集觀上看”，把每個迴圈節設成A，這一類裡的所有環排列就都是一樣的，從微觀上看，迴圈節內部可以不同，而迴圈節內部的不同造就相同迴圈節長度下不同的種類（題目中所說的種類）。而迴圈節所有可能的長度是n的所有因子，也就是對所有i而言的gcd(i ,n)，而num（迴圈節長度）就是該長度下有多少種可能的迴圈節。這裡的num（）和另一位博主的g（）是一樣的，第二個等號的意思如下：

設gcd（i,n）= d

則gcd（i/d,n/d）= 1

有d 個位置的旋轉同構環坐人種類數g(d) 的和，

根據乘法分配律，寫成k*g(di) 的和，k為整個求和式子中g(di)的個數，

其中k為尤拉函式。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
#define mod 1000000007ll 
typedef long long ll;
struct Mat
{
    ll mat[3][3];
    int row,col;
};
Mat mod_mul(Mat a,Mat b,int p)
{
    Mat ans;
    ans.row=a.row;
    ans.col=b.col;
    memset(ans.mat,0,sizeof(ans.mat));
    for(int i=0;i<ans.row;i++)      
        for(int k=0;k<a.col;k++)
            if(a.mat[i][k])
                for(int j=0;j<ans.col;j++)
                {
                    ans.mat[i][j]+=a.mat[i][k]*b.mat[k][j]%p;
                    ans.mat[i][j]%=p;
                }
    return ans;
}
Mat mod_pow(Mat a,int k,int p)
{
    Mat ans;
    ans.row=a.row;
    ans.col=a.col;
    for(int i=0;i<a.row;i++)
        for(int j=0;j<a.col;j++)
            ans.mat[i][j]=(i==j);
    while(k)
    {
        if(k&1)ans=mod_mul(ans,a,p);
        a=mod_mul(a,a,p);
        k>>=1;
    }
    return ans;
}
#define maxn 55555
int euler[maxn],prime[maxn],res;
void Get_euler(int n)
{
    memset(euler,0,sizeof(euler));
    euler[1]=1;
    res=0;
    for(int i=2;i<=n;i++)
    {
        if(!euler[i])euler[i]=i-1,prime[res++]=i;
        for(int j=0;j<res&&prime[j]*i<=n;j++)
        {
            if(i%prime[j]) euler[prime[j]*i]=euler[i]*(prime[j]-1);
            else
            {
                euler[prime[j]*i]=euler[i]*prime[j];
                break;
            }
        }
    }
}
ll f[maxn];
void init()
{
    Get_euler(50000);
    f[1]=1,f[2]=3;
    for(int i=3;i<=50000;i++)f[i]=(f[i-1]+f[i-2])%mod;
}
ll get_f(int n)
{
    if(n<=50000)return f[n];
    Mat A;
    A.row=A.col=2;
    A.mat[0][0]=1,A.mat[0][1]=1,
    A.mat[1][0]=1,A.mat[1][1]=0;
    A=mod_pow(A,n-2,mod);
    return 3ll*A.mat[0][0]+A.mat[0][1];
}
ll get_euler(int n)
{
    if(n<=50000)return euler[n];
    ll ans=n;
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
        {
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
ll Mod_pow(ll a,ll b)
{
    a%=mod;
    ll ans=1ll;
    while(b)
    {
        if(b&1)ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
int main()
{
    init();
    int n;
    while(~scanf("%d",&n))
    {
        if(n==1)
        {
            printf("2\n");
            continue;
        }
        ll ans=0;
        for(int i=1;i*i<=n;i++)
            if(n%i==0)
            {
                ll temp=(get_f(i))%mod*get_euler(n/i)%mod;
                ans=(ans+temp)%mod;
                if(i*i!=n)
                {
                    int j=n/i;
                    temp=get_f(j)*get_euler(n/j)%mod;
                    ans=(ans+temp)%mod;
                }           
            }
        printf("%I64d\n",ans*Mod_pow(n,mod-2)%mod);
    }
    return 0;
}

引用：https://blog.csdn.net/v5zsq/article/details/52554569