匈牙利算法、KM算法
PS:其實不用理解透增廣路,交替路,網上有對代碼的形象解釋,看懂也能做題,下面我盡量把原理說清楚
基本概念 (部分來源、部分來源)
二分圖: 設G=(V,E)是一個無向圖,如果頂點V可分割為兩個互不相交的子集(A,B),並且圖中的每條邊(i,j)所關聯的兩個頂點i和j分別屬於這兩個不同的頂點集(i in A,j in B
),則稱圖G為一個二分圖。

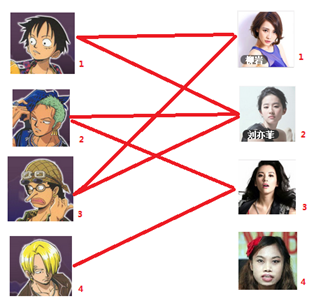
匹配: 一個匹配即一個包含若幹條邊的集合,且其中任意兩條邊沒有公共端點。下圖標紅的邊即為匹配

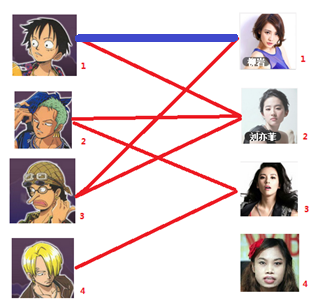
? 最大匹配: 匹配數最大,如下圖有4條匹配邊
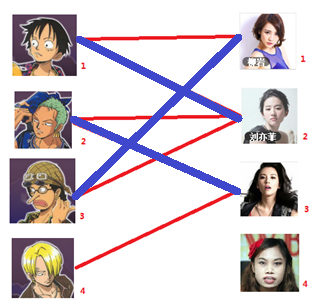
? 完全匹配: 即所有的頂點都是匹配點,上圖(Fig.4)即為完全匹配,不是所有的圖都存在完全匹配
? 交替路:
? 增廣路(也稱增廣軌或交錯軌): 如果交替路經過除出發點外的另一個未匹配點,則這條交替路稱為增廣路,如交替路概念的例子,其途徑點8,即為增廣路
匈牙利算法
由增廣路的定義推出下面三個結論(設P為一條增廣路):
1). P的路徑長度一定為奇數,第一條邊和最後一條邊都是未匹配的邊(根據要途經已匹配的邊和要經過另一個未匹配點,這個結論可以理解成第一個點和最後一個點都是未匹配點,可以在Fig.3上的增廣路觀察到)
2). P經過取反操作可以得到一個更大的匹配圖(取反操作即,未匹配的邊變成匹配的邊,匹配的邊變成未匹配的邊,這個結論根據結論1).和交替路概念可得該結論)
3). 當且僅當不存在關於圖M的增廣路徑,則圖M為最大匹配
算法思路:不停找增廣路,並增加匹配的個數
代碼過程模擬(圖片來源)
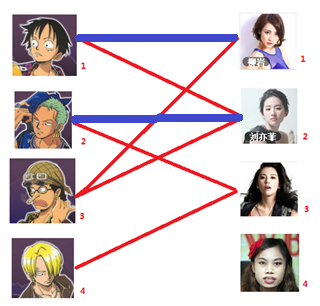
這裏就解釋第三幅圖到第四幅圖的過程,註意這裏的過程就是找增廣路。圖三開始,男3可以匹配女1,(男3 -> 女1),發現女1已經跟男1匹配(男3 -> 女1 -> 男1),看到男1可以跟女2匹配(註意從開始到現在的是未匹配邊,匹配邊,未匹配邊)這樣走下去,路徑是男3 -> 女1 -> 男1 -> 女2 -> 男2 -> 女3,此時是以未匹配邊結束且找不到匹配邊了。
求最大匹配的模板
#include <iostream> #include <algorithm> using namespace std; const int MAXN = 105; int x, y, mp[MAXN][MAXN]; int mx[MAXN], my[MAXN];//x 跟哪個 y 匹配s int vis[MAXN];//一條增廣路中哪些 y 點被訪問過 int dfs(int a) { for(int i = 1;i <= n;++i) { //先找出與 a 點有聯系且沒被訪問過的 y 點 if(!vis[i] && mp[a][i]) { vis[i] = 1; //然後從就是 x -> i -> my[i] 構造這條增廣路,接著就是 dfs(my[i]),重復以上操作 //根據增廣路的結論,如果存在增廣路,那麽最後 my[i] == 0,即為未匹配點 //然後將其賦新值,根據 DFS 遞歸各層,該賦值即為增廣路中進行取反操作,未匹配邊變為匹配邊 //至於匹配邊變為未匹配邊,my[i] 被賦新值 //若不存在增廣路,那麽就沒進行賦值,即不取反 if(!my[i] || dfs(my[i])) { my[i] = a; return 1; } } } return 0; } int solve() { int ret = 0; fill(mx, mx + MAXN, 0); fill(my, my + MAXN, 0); //剛開始的 x 都是未匹配點 //vis 每次清零,vis 就是增廣路中的 y 點 for(int i = 1;i <= x;++i) { fill(vis, vis + MAXN, 0); ret += dfs(i); } return ret; }
求最大匹配的模板題
#include <iostream>
#include <cstring>
using namespace std;
const int MAXN = 505;//這題數組要開大
int x, y, mp[MAXN][MAXN];
int mx[MAXN], my[MAXN];//x 跟哪個 y 匹配s
int vis[MAXN];//一條增廣路中哪些 y 點被訪問過
int dfs(int a)
{
for(int i = 1;i <= y;++i)
{
if(!vis[i] && mp[a][i])
{
vis[i] = 1;
if(!my[i] || dfs(my[i]))
{
my[i] = a;
return 1;
}
}
}
return 0;
}
int solve()
{
int ret = 0;
memset(mx, 0, sizeof(mx));
memset(my, 0, sizeof(my));
for(int i = 1;i <= x;++i)
{
fill(vis, vis + MAXN, 0);
ret += dfs(i);
}
return ret;
}
int main()
{
int n;
cin >> n;
while(n--)
{
cin >> x >> y;
memset(mp, 0, sizeof(mp));
int num, t;
for(int i = 1;i <= x;++i)
{
cin >> num;
while(num--)
{
cin >> t;
mp[i][t] = 1;
}
}
if(solve() == x)
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}時間復雜度:鄰接矩陣最壞O(n ^ 3), 鄰接表O(nm)
空間復雜度:鄰接矩陣O(n ^ 2), 鄰接表O(n + m)
擴展:匈牙利算法也可以看成DFS過程,參考
KM算法
該算法是求帶權二分圖的最大權匹配
此篇易懂,新概念少,沒代碼,概念看不懂的,建議先看左邊易懂那篇再來,這個是代碼篇
頂標:設頂點 Xi 的頂標為 A[i],頂點 Yi 的頂標為 B[j],頂點 Xi 與 Yj 之間的邊權為 w[i][j],初始化時,A[i] 的值為與該點關聯的最大邊權值,B[j] 的值為0
相等子圖:選擇 A[i] + B[j] = w[i][j] 的邊 <i, j> 構成的子圖,就是相等子圖
算法執行過程中,對任一條邊<i, j>,A[i] + B[j] >= w[i][j] 恒成立,這個下面圖示解釋清楚
這裏的算法介紹是用slack[j]數組優化過,slack數組存的數是Y部的點相等子圖時,最小要增加的值
沒有優化過的容易理解,代碼量也短,去原博客先看完沒有優化的會更容易理解優化過的代碼
算法圖示:
給個二分圖,只取邊權跟頂標相等的邊,邊權值跟頂標理解為工作效率

看到員工B,B與c以外的其他工作嘗試匹配後,頂標和,即上面說的A[i] + B[j] >= w[i][j],並且最小的差值為1,該差值存在slack數組裏,當B與c嘗試匹配,因為A -> c,就能找到一條增廣路,B -> c -> A -> a,此時A只有找到a匹配,但是A -> a 的頂標和 = 4 也是大於邊權值 3,與slack數組比較,存儲最小的差值1。
因為能夠進行匹配的是相等子圖,即不存在此相等子圖的減少量,所以遍歷未匹配的Y部的slack數組,找出最小的減少量minz。我們要使總的工作效率盡可能地高,即減少地少。
若X部的點還未匹配,就將增光路中X部減去minz,即下圖中A、B都減去1,Y部加上minz,再進行嘗試匹配,註意,匹配成功的話,A[i] + B[j] = w[i][j]

其實下面這圖不符合匈牙利算法的具體過程,由於這裏只要理解結果,就拿下面這圖了,這裏X部+Y部的頂標值 = 對應點的邊權值。正確的連接應該是(看上圖),B -> c, A -> a,因為根據匈牙利算法所形成的增廣路應該是 B -> c -> A -> a, 在這條增廣路中只有 A -> c是匹配的,然後取反,就B -> c, A -> a

由於圖到此就錯了,所以就不繼續貼流程圖,直接上結果圖,具體過程如上重復

下面是以上推薦博客的代碼,跑了一遍測試,我就把maxn改了
#include<iostream> #include<cstring> #include<cstdio> #include<vector> #include<map> using namespace std; typedef long long ll; const int maxn = 300 + 10; const int INF = 0x3f3f3f3f; int wx[maxn], wy[maxn];//每個點的頂標值(需要根據二分圖處理出來) int cx[maxn], cy[maxn];//每個點所匹配的點 int visx[maxn], visy[maxn];//每個點是否加入增廣路 int cntx, cnty;//分別是X和Y的點數 int Map[maxn][maxn];//二分圖邊的權值 int slack[maxn];//邊權和頂標最小的差值 bool dfs(int u)//進入DFS的都是X部的點 { visx[u] = 1;//標記進入增廣路 for(int v = 1; v <= cnty; v++) { if(!visy[v] && Map[u][v] != INF)//如果Y部的點還沒進入增廣路,並且存在路徑 { int t = wx[u] + wy[v] - Map[u][v]; if(t == 0)//t為0說明是相等子圖 { visy[v] = 1;//加入增廣路 //如果Y部的點還未進行匹配 //或者已經進行了匹配,可以從原來的匹配反向找到增廣路 //那就可以進行匹配 if(cy[v] == -1 || dfs(cy[v])) { cx[u] = v; cy[v] = u;//進行匹配 return 1; } } else if(t > 0)//此處t一定是大於0,因為頂標之和一定>=邊權 { slack[v] = min(slack[v], t); //slack[v]存的是Y部的點需要變成相等子圖頂標值最小增加多少 } } } return false; } int KM() { memset(cx, -1, sizeof(cx)); memset(cy, -1, sizeof(cy)); memset(wx, 0, sizeof(wx));//wx的頂標為該點連接的邊的最大權值 memset(wy, 0, sizeof(wy));//wy的頂標為0 for(int i = 1; i <= cntx; i++)//預處理出頂標值 { for(int j = 1; j <= cnty; j++) { if(Map[i][j] == INF)continue; wx[i] = max(wx[i], Map[i][j]); } } for(int i = 1; i <= cntx; i++)//枚舉X部的點 { memset(slack, INF, sizeof(slack)); while(1) { memset(visx, 0, sizeof(visx)); memset(visy, 0, sizeof(visy)); if(dfs(i))break;//已經匹配正確 int minz = INF; for(int j = 1; j <= cnty; j++) if(!visy[j] && minz > slack[j]) //找出還沒經過的點中,需要變成相等子圖的最小額外增加的頂標值 minz = slack[j]; //和全局變量不同的是,全局變量在每次while循環中都需要賦值成INF,每次求出的是所有點的最小值 //而slack數組在每個while外面就初始化好,每次while循環slack數組的每個值都在用到 //在一次增廣路中求出的slack值會更準確,循環次數比全局變量更少 //還未匹配,將X部的頂標減去minz,Y部的頂標加上minz for(int j = 1; j <= cntx; j++) if(visx[j])wx[j] -= minz; for(int j = 1; j <= cnty; j++) //修改頂標後,要把所有不在交錯樹中的Y頂點的slack值都減去minz if(visy[j])wy[j] += minz; else slack[j] -= minz; } } int ans = 0;//二分圖最優匹配權值 for(int i = 1; i <= cntx; i++) if(cx[i] != -1)ans += Map[i][cx[i]]; return ans; } int n, k; int main() { while(scanf("%d", &n) != EOF) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) scanf("%d", &Map[i][j]); } cntx = cnty = n; printf("%d\n", KM()); } return 0; }
匈牙利算法、KM算法