【計導非課系列】 第六節 演算法 資料結構

程式=演算法+資料結構

眾所周知，完美的程式是由優秀的演算法和良好的資料結構組成的。什麼是演算法？什麼是資料結構？這裡，我們將一起探索演算法和資料結構的奧祕，初步揭開它們的神祕面紗。

當然，演算法和資料結構可以作為永遠發展的大事業，絕非寥寥數語能夠說清楚的。

博文目錄

演算法

• 什麼是演算法
• 流程圖
• 基本演算法

資料結構

• 基本資料結構 ADT 連結串列 棧 堆 樹 圖
• 高階程式設計語言
• 軟體工程
• 演算法案例（腦洞大開）

before we start…

人類是怎麼樣讓計算機解決問題？怎樣操作？
首先，分析問題的本質。我要幹些什麼？知道我要幹什麼之後，我需要想想怎麼去實現這些東西，我要有一個明確的構思，現在不一定需要太具體的細節，只需要大概。之後捏，程式猿就可以大顯身手咯，編寫程式把之前說好的演算法給實現——具體是怎麼做的，怎麼寫出來。之後就可以運行了，執行之後就可以得到結果了，當然極有可能經歷過很多很多次的debug！

在這個過程中，怎麼實現這件事情就叫做演算法——一種逐步解決問題或完成任務的方法。

演算法可以精化——每一步是怎麼實現的；也可以泛化——我大概想怎麼做，重複這一堆動作。

演算法

演算法的定義

演算法是一組明確步驟

的有序集合，它產生結果，並在有限的時間內終止。
演算法的5個特性：有窮性 確定性 輸入 輸出 可行性
另一種定義：（瞭解一下）給定問題和裝置，一個演算法是用該裝置可以理解的語言表示的。解決這個問題的一種方法是精確刻畫的。演算法具有以下屬性：
1.應用於一個具體的輸入集合或將問題描述在有窮步動作之後得到結果
2.有一個唯一的初始動作
3.每一個動作有一個唯一的後繼動作
4.該序列終止時或者得到這個問題的解，或者因該問題不可解而獲得不可解說明

演算法的精化 泛化

演算法的精化：就是將每一步詳細地寫出來

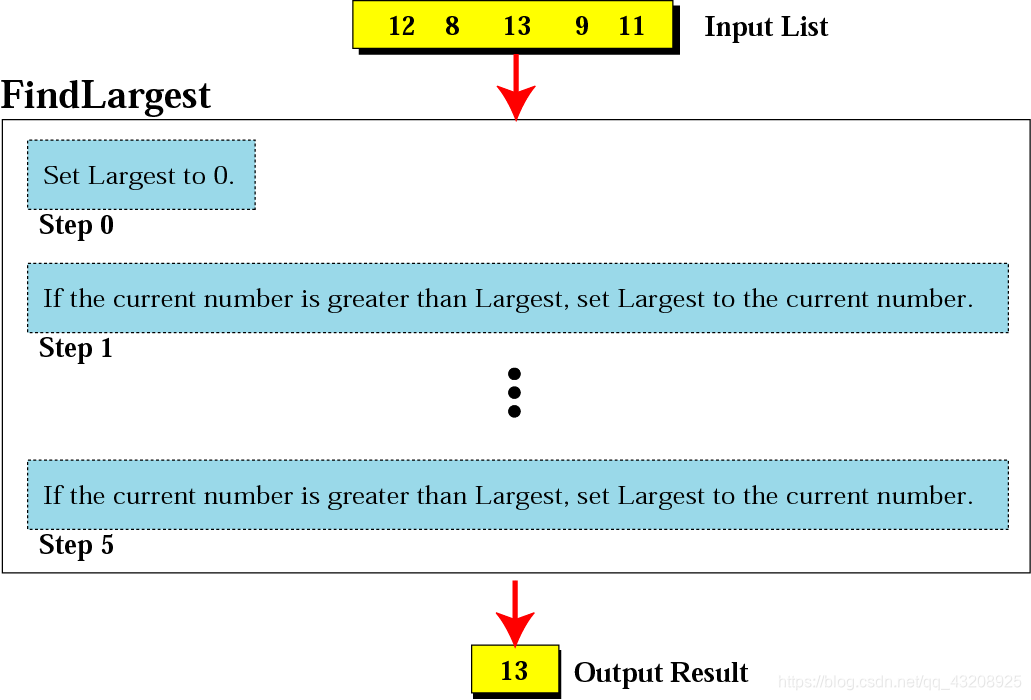
演算法的泛化：大致描述一個程式具體需要怎麼做，比如
Repeat the following step N times:
If the current number is greater than Largest, set it to the current number.

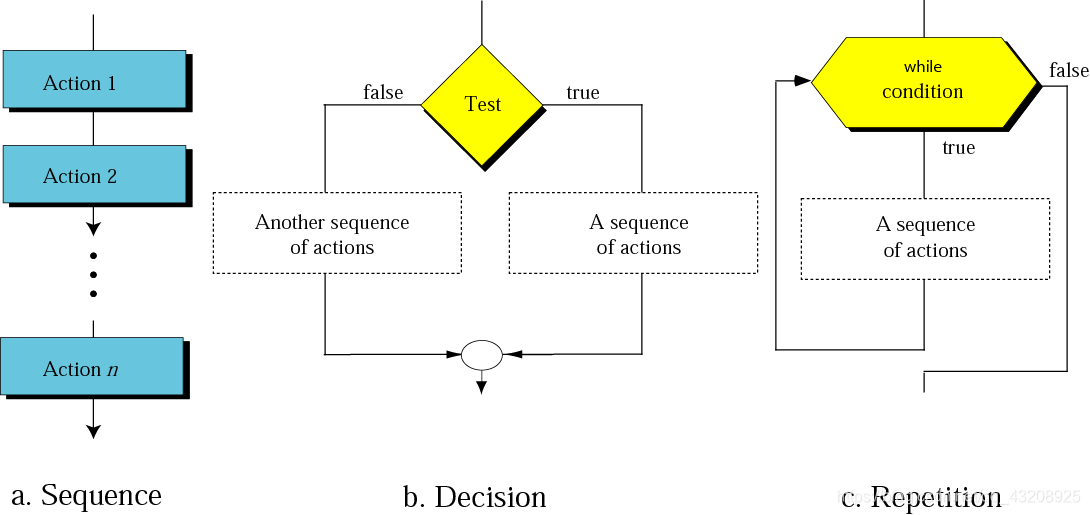
演算法的基本結構

• 順序 Sequence
• 選擇 Decision
• 迴圈 Repetition

流程圖

寫程式之前畫好流程圖，這樣可在寫程式碼的時候讓程式更加結構清晰。

虛擬碼：不管細節 只關心大體實現

是在編寫演算法時，為了更好地表示演算法本身，不在一些小的細節上糾纏，而採用類似於英語（或其他自然語言）表示演算法的演算法表示方法。

子演算法（函式）：實現結構化程式設計

在結構化程式設計時使用模組化或分單元的辦法來構成程式，這些被分成的小單元稱之為子演算法。
每個子演算法又可以劃分為更小的子演算法，這個過程持續到子演算法變為最本質的（可被立即理解的）描述為止。
優點：
使程式更易理解
可以在主演算法不同的地方呼叫
其實，子演算法就是我們平常所說的函式。
舉個例子：

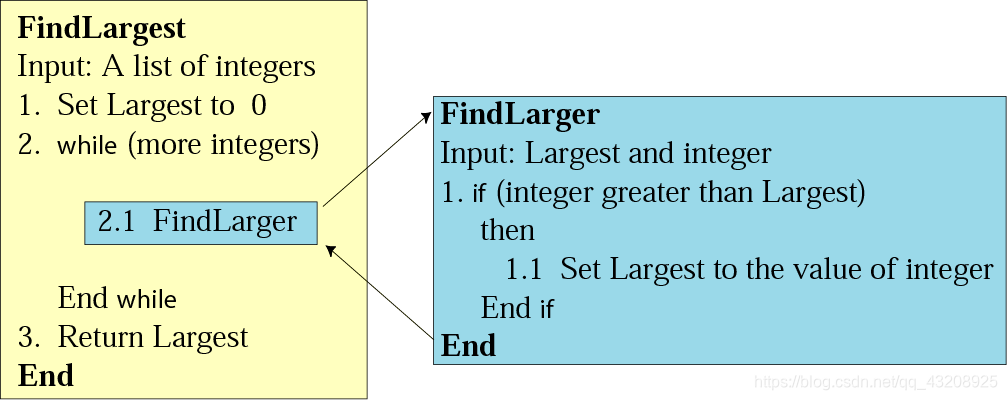
結構圖和流程圖

結構圖：高層設計工具

結構圖能很好地表示程式設計者的邏輯思維的過程；把演算法中各個模組之間的關係表示得更加清楚。
結構圖的常用圖示：

舉例：結構圖可以把大程式要實現的所有東西都表示出來，高屋建瓴

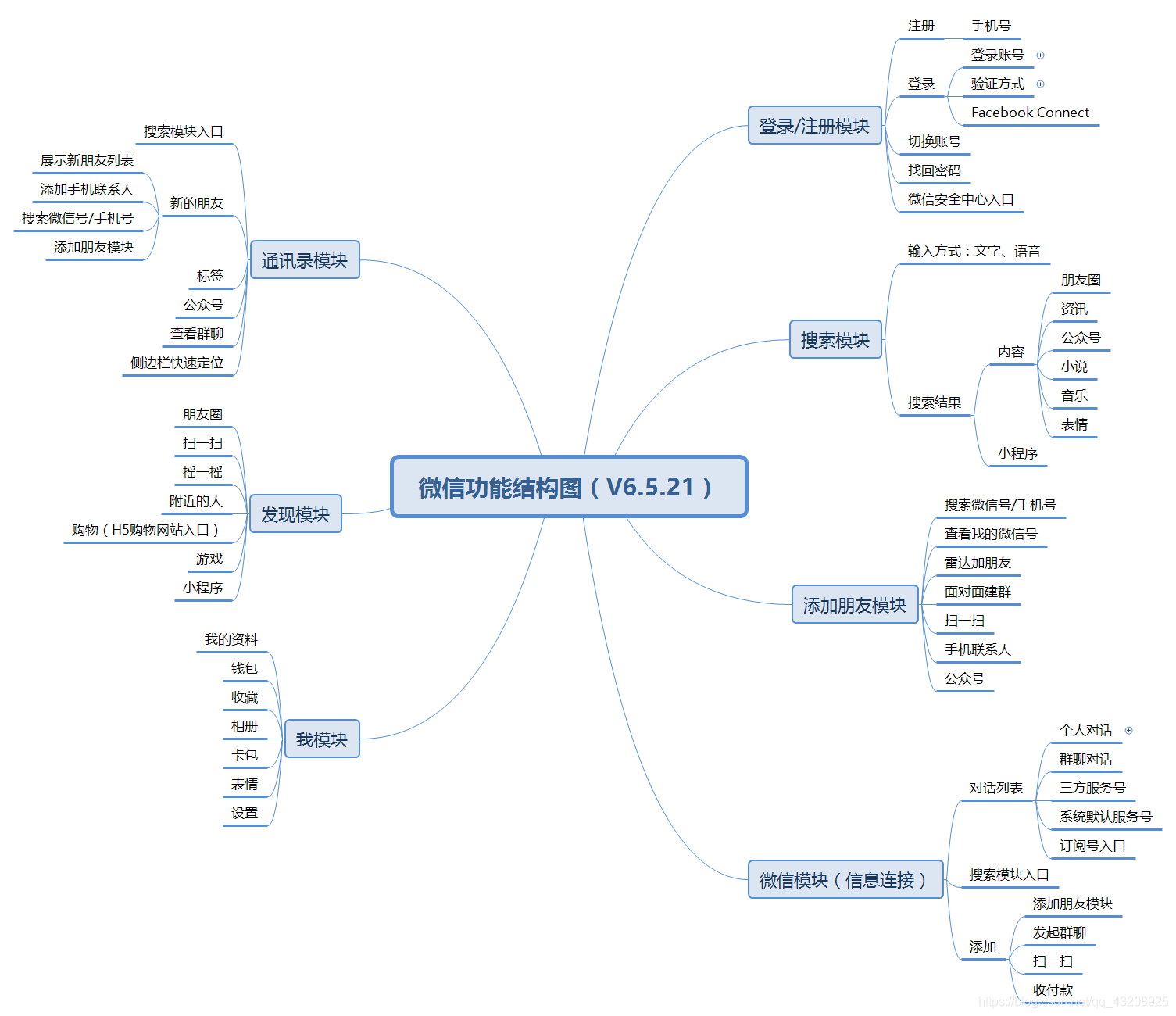
流程圖：表示演算法的工具

用一些圖框來表示各種操作
用圖形表示演算法，直觀形象，容易理解

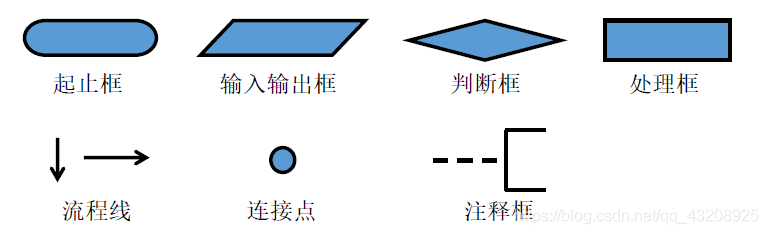
基本演算法

基本演算法包括求和、乘積、最大最小、排序、查詢
排序包括氣泡排序，選擇排序，插入排序

求和、求積

把初始結果設定為0或者1，然後設定一個變數記錄執行了多少次。之後執行迴圈。

排序

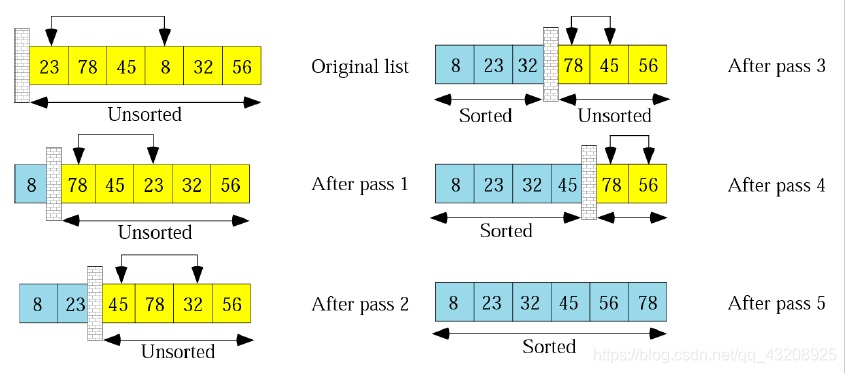
氣泡排序：小的資料上升

之前寫過一篇關於氣泡排序的部落格，傳送門：
https://blog.csdn.net/qq_43208925/article/details/83684040
它重複走訪要排序的數列，一次比較兩個元素，順序不對的話就把他們交換過來。直到某一次走訪發現全部順序都是對的。
這樣的直觀感受是，大數像石頭一樣沉澱，小數像泡泡一樣“浮出水面”，因此得名“氣泡排序”。
實現原理：
給定N個數，那麼它最多需要執行N-1次（因為最後一個一定不需要再次排列）迴圈，每次迴圈是一輪。如果某一輪中已經出現了沒有交換，則可以提前結束。因此需要一個flag變數，記錄迴圈狀態。
在每一輪迴圈中，從第一個數開始，與下一個數進行比較。一直到上一次沉底的元素。上一次沉底的元素一定不需要排列，因為它一定會是最大的。

下面兩個例子（第一個摘自之前的部落格），第一個是讓大數沉底，第二個是讓小數上升。

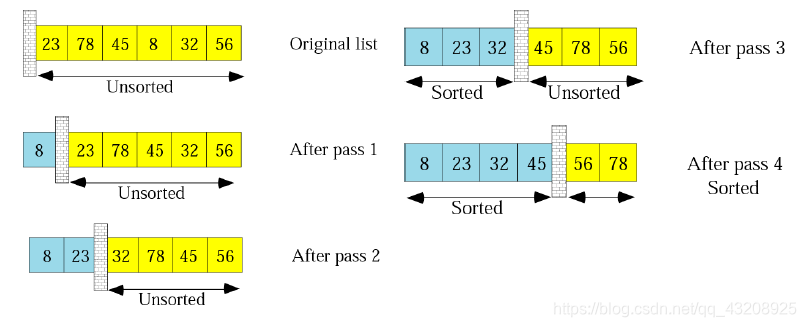
插入排序：按順序走訪，把後面的資料放到前面已經排好序的陣營裡面，一個一個插進去

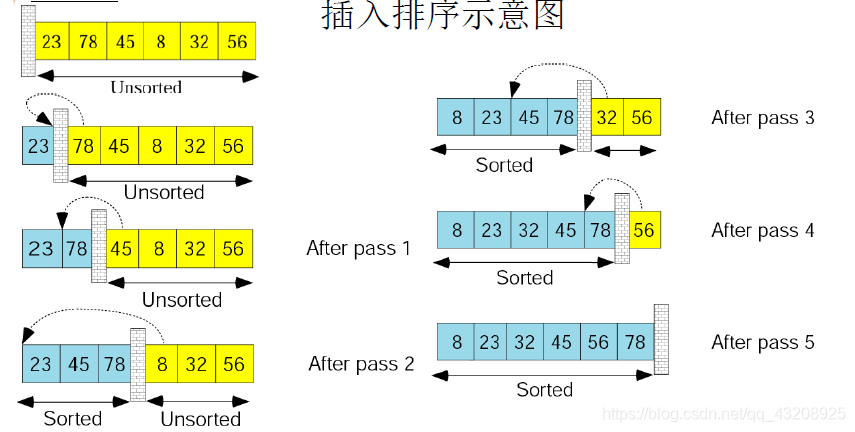
逐個排序

選擇排序：遍歷，每次選出來一個最大/最小，放到排好序的陣營裡面

這和氣泡排序的區別：氣泡排序是逐個走訪，看到誰不對就順手換過來了；而選擇排序是這一次迴圈裡面我偏偏要找到最大/最小的那一個，把他拎出來。

查詢

在一些（有序的/無序的）資料元素中，通過一定的方法找出與給定關鍵字相同的資料元素的過程叫做查詢。

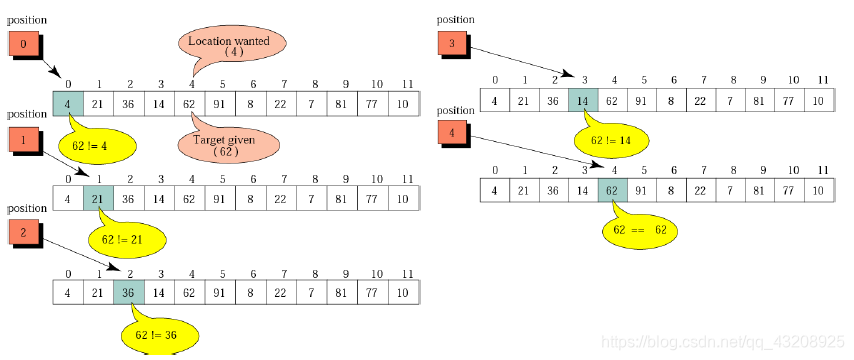
順序查詢

從第一個/最後一個開始遍歷，直到出現了我想要的。

折半查詢（二分查詢） Binary search

在有序陣列中查詢。

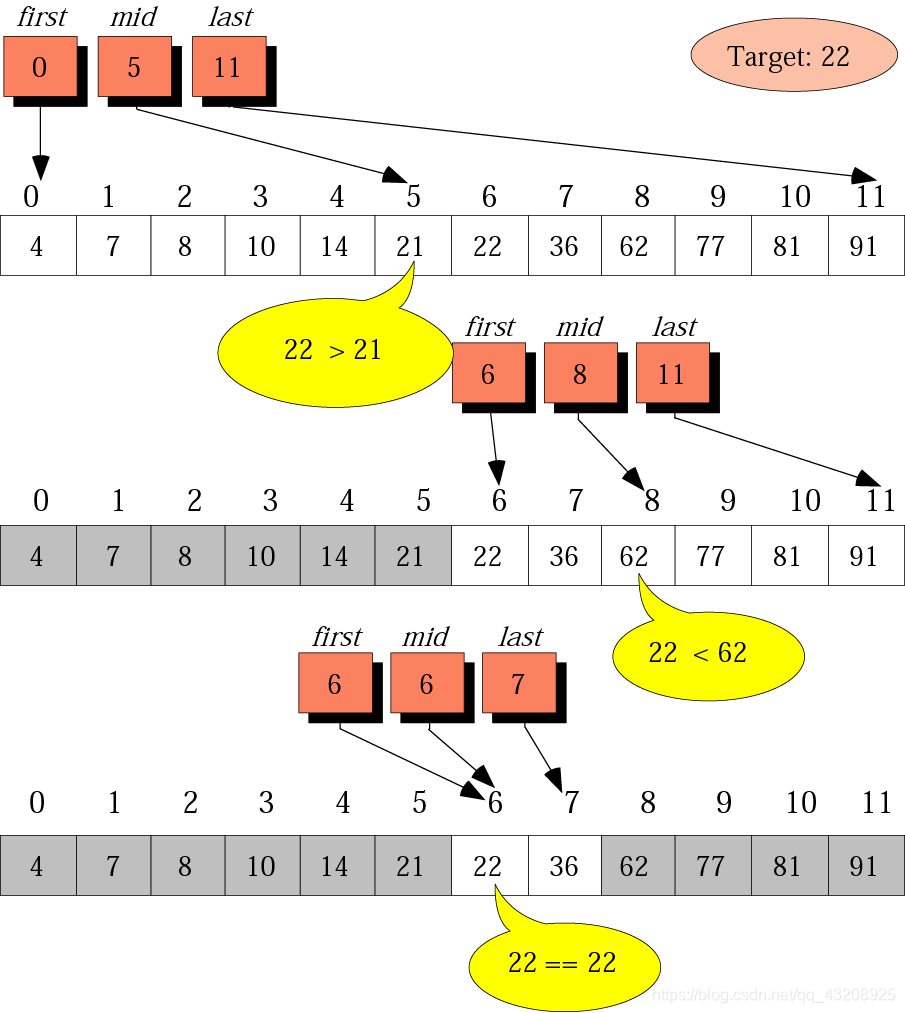
需要變數三個：first,mid,last，給定了target。
首先，target和mid去比較，如果mid大於target，那麼first變成mid+1；
如果mid小於target，那麼last變成mid-1。

遞迴、迭代演算法

迭代是重複反饋過程的活動，其目的通常是為了逼近所需目標或結果。每一次對過程的重複稱為一次“迭代”，而每一次迭代得到的結果會作為下一次迭代的初始值。
遞迴（Recursion）：演算法中包含了對演算法自身的呼叫的演算法。
分治演算法（Divide and Conquer）：將一個難以直接解決的大問題，通過分析，分解為一些規模較小的相同問題，進而對各個小問題進行解決，最後達到整個問題的解決。

迭代，就是不斷更新，不斷更新。
f2=f1
f3=f2
放到迴圈裡，就可以構成迭代。

遞迴，就是函式自己呼叫自己，這個過程往往特別心酸。

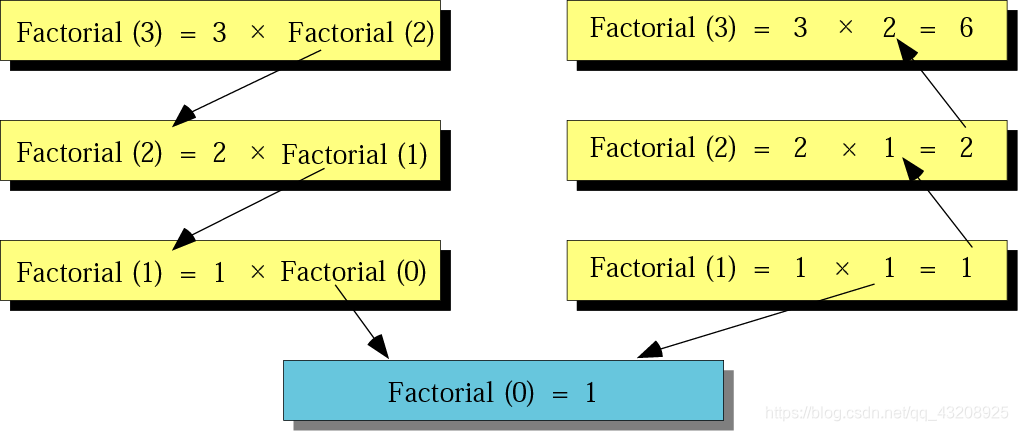
分治法是資料結構中用到的方法，把大問題分成很多小塊。

計算的複雜性：運用的初等運算的步數

時間複雜度

•O(1)稱為常數級；
•O(log n)稱為對數級；
•O(n)稱為線性級；
•O(nc)稱為多項式級（C為常數）；
•O(Cn)稱為指數級（C為常數）；
•O(n!)稱為階乘級

空間複雜度

臨時佔用了多少儲存空間

資料結構

陣列 array

什麼是陣列？
首先，顧名思義，一組數字。陣列放到了連續的一塊兒上，而且還有順序。這就是陣列。
陣列可以實現批量處理資料，所以很有優勢。
陣列分為一維和二維的，當然還有更多。對於二維陣列，在記憶體中是怎麼儲存的呢？
逐行儲存。陣列對於行來說，記憶體是連續的。
陣列一旦確定，大小不能被改變！！

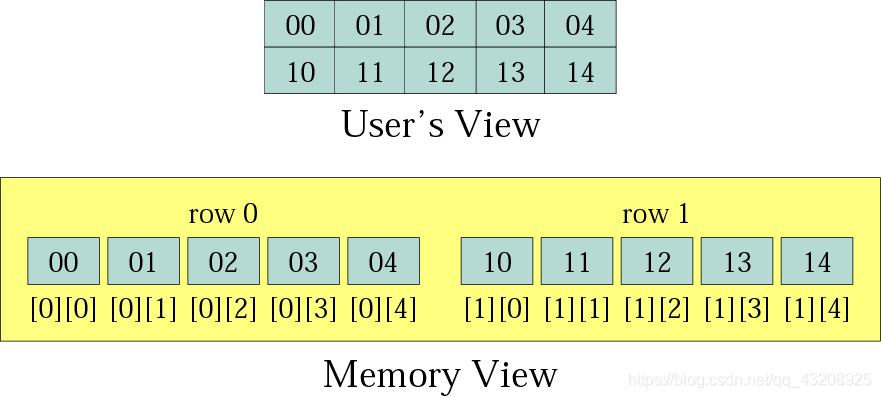
逐行儲存。

連結串列 linked list

什麼是連結串列？顧名思義，不就是連結在一起形成的表嘛。
既然我們有了陣列存放資料，那麼為什麼會出現連結串列？看起來還更麻煩一些呢……
陣列有一個巨大的缺陷，那就是不能夠改變大小。可是我一開始不知道要儲存多少資料，怎麼辦？
只能先讓這個陣列變得很大很大，大到能夠滿足我的需要。
但是，我怎麼知道有多大？還有，一開始開闢了很大的記憶體空間，一直等著給他賦值。不去賦值的話，那些空間不久白白浪費掉了？
所以，我需要一個辦法，能夠改變長度，而且不造成資源的浪費。
連結串列就是一種解決方案。

連結串列的定義

是一個有序的集合，其中每一個元素都包含下一個元素的地址，由資料和指標（地址）構成。

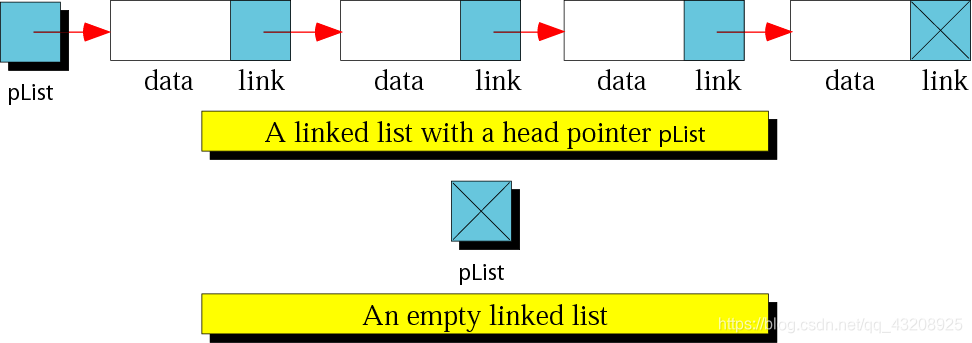
圖中每一個方塊叫做一個節點——基本的單位。
每個節點包括兩個東西：一，我要儲存的資料；二，下一個元素的地址，也就是下一個元素在哪兒。

對連結串列的操作

• 插入節點
  為新節點分配記憶體、寫入資料
  使新節點指向後繼節點，使前一個節點指向新節點。
  
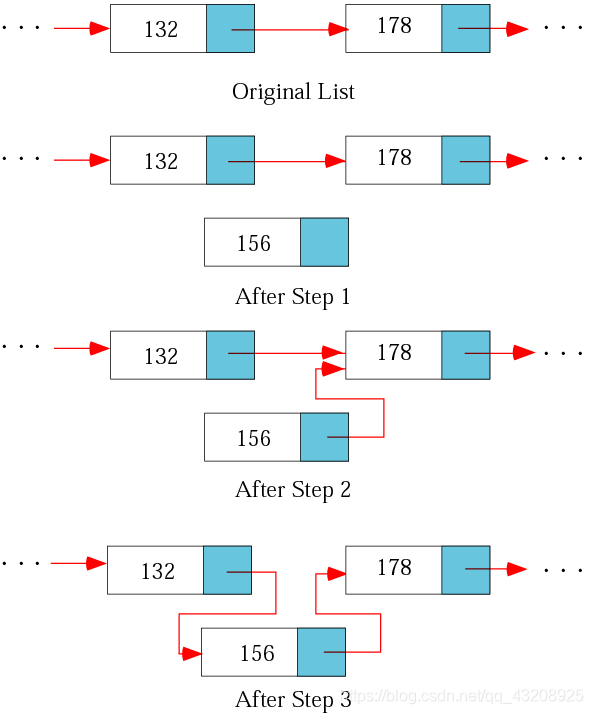
• 刪除節點
  定位要刪除的節點
  將前一個的指標指向被刪除的節點的後繼節點
  之後可以釋放掉被刪除節點的記憶體空間
  注意：刪除第一個節點或僅有的單個節點時要特殊處理。比如刪除最後一個的時候需要讓前一個指向NULL，刪除僅有的一個的時候，需要讓Header直接指向NULL。
• 遍歷連結串列
  需要一個叫做Walker的東西，從Header出發，之後沿著指標走。
  這種遍歷只能從第一個開始，一直到最後一個。

連結串列在記憶體中儲存可以不連續

因為有了指標，解決了定位的問題，這樣對於記憶體可以更加了靈活地使用。

抽象資料型別 ADT

咱們用線性表，用樹，用圖多了，用的多了就會被抽象出來，這就是ADT。
人們經過抽象出一類類具有一定固定模式的資料表示法，將其模型化，形成公共模板功能，供大家使用，使用者只需知道一個數據型別能做什麼，而不必知道其怎樣做。
結構：資料生命、操作宣告、封裝資料和操作
封裝，就是把它們實現到我的程式中。

常見：線性表 樹 圖

線性表

插入 刪除 檢索 遍歷

棧——乾草堆

限制線性表 只能在一端實現新增刪除 LIFO 後入先出
（怎麼理解，很難？或許，可以這樣理解——）
棧的英文是stack，本義是乾草堆。
乾草堆啥樣？我先放進去的乾草在最底下，我之後放上去的乾草放在最上面。
那麼，如果我現在想要拿一些乾草走，我最先拿到的是那一部分？最先放上去的還是最後放上去的？
最後啊！
這就是後入先出的字面解釋。
最後進去的，最先被拿出來。
這樣一說，是不是理解了很多呢？
棧的操作

• Push 壓棧\入棧
  
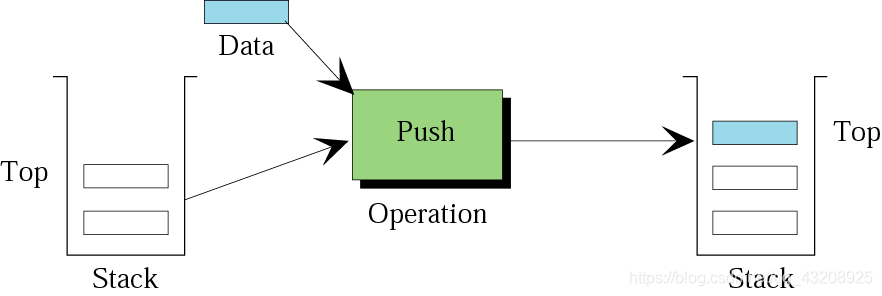
• Pop 出棧
• 

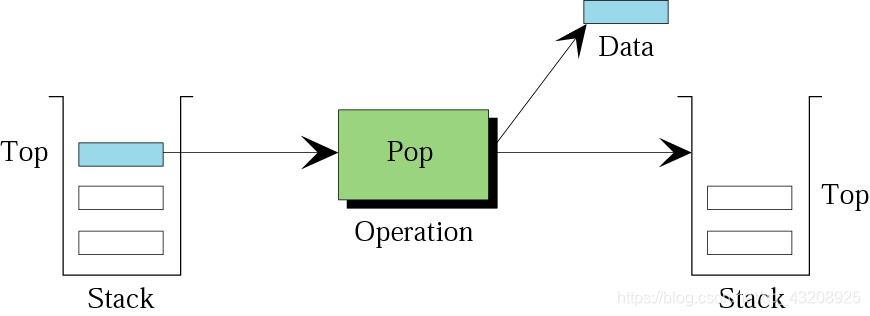
佇列——排隊買飯

兩端都需要操作，但是隻能一端進，另一端出。 FIFO

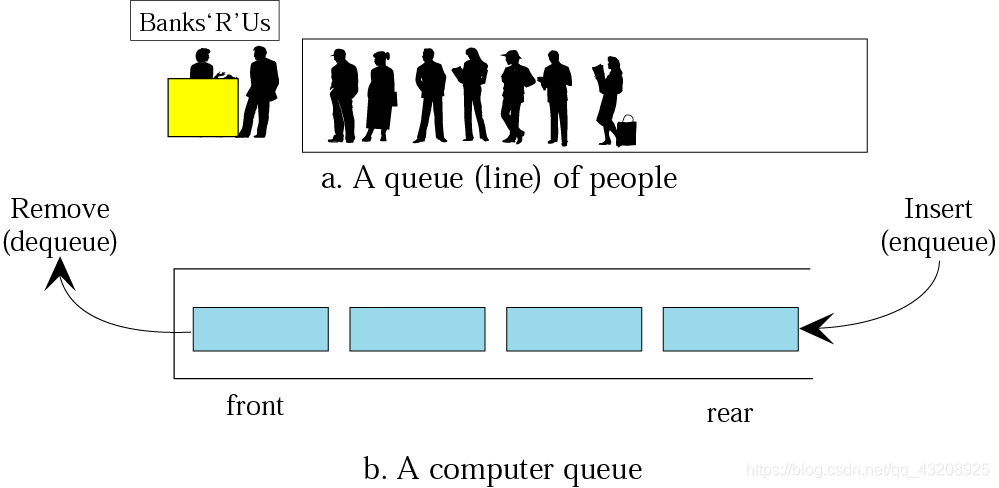
佇列的操作：

• 入列 Enqueue
• 出列Dequeue
• 空

樹——北林最離不開的東西

內容：

• 節點：組成樹的有限元素
• 分支：連線節點的有向線段
• 度：與節點連線的分支數目。指向節點：入度，離開節點：出度。
• 子樹：根節點下面還有可以形成樹的東西
  
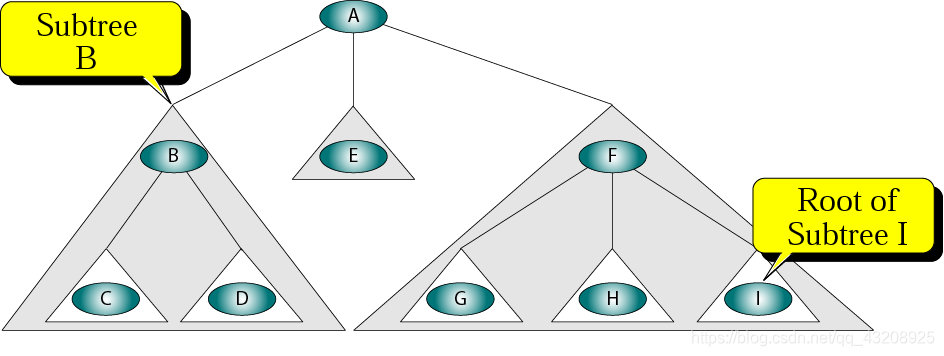
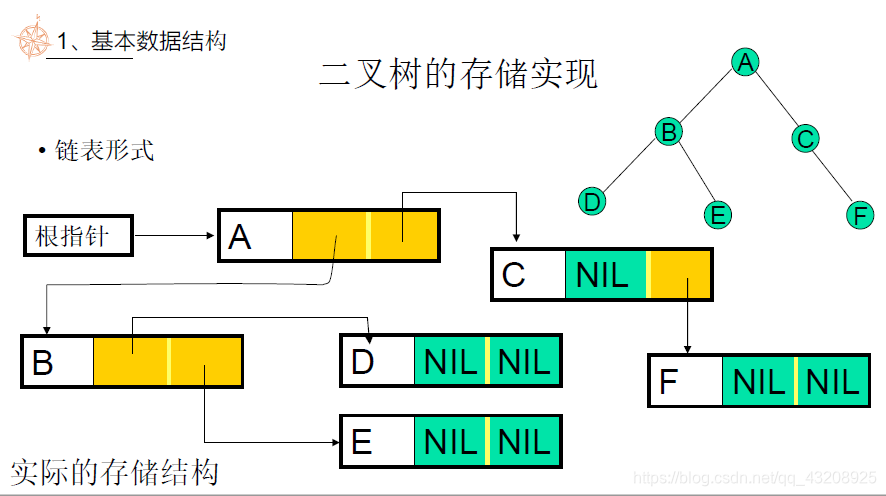
  二叉樹：
  每個節點最多左右兩個子樹。
  
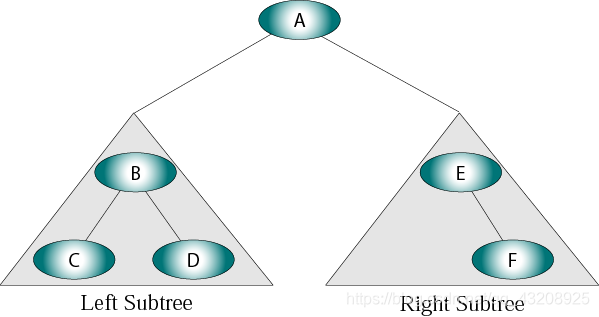
  用連結串列實現二叉樹：
  每個節點包括三個東西：儲存的資料，左子樹的地址，右子樹的地址。
  不完全儲存會浪費記憶體空間。
  

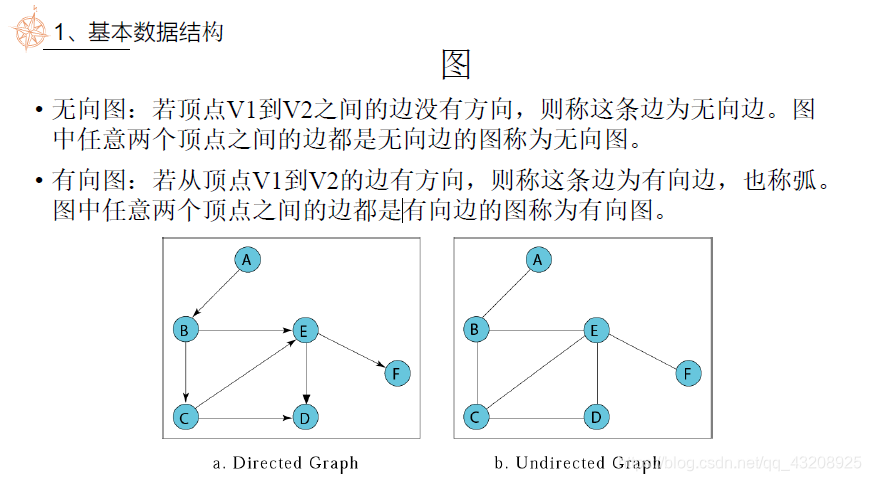
圖——關係不再單純

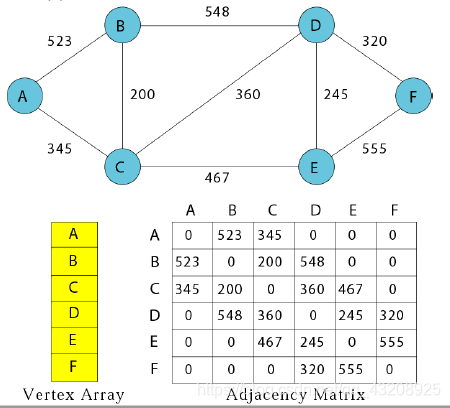
儲存實現：鄰接矩陣

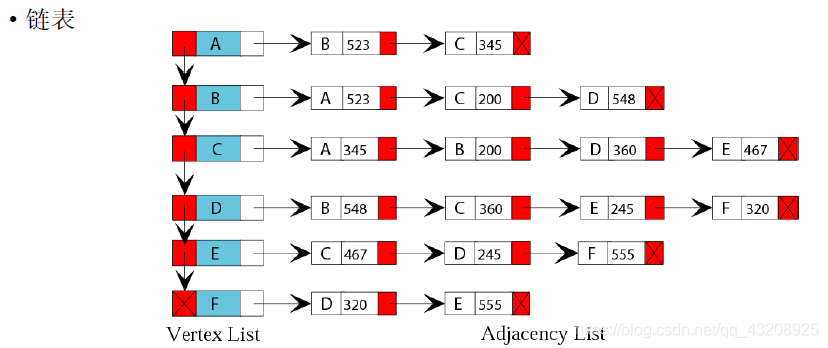
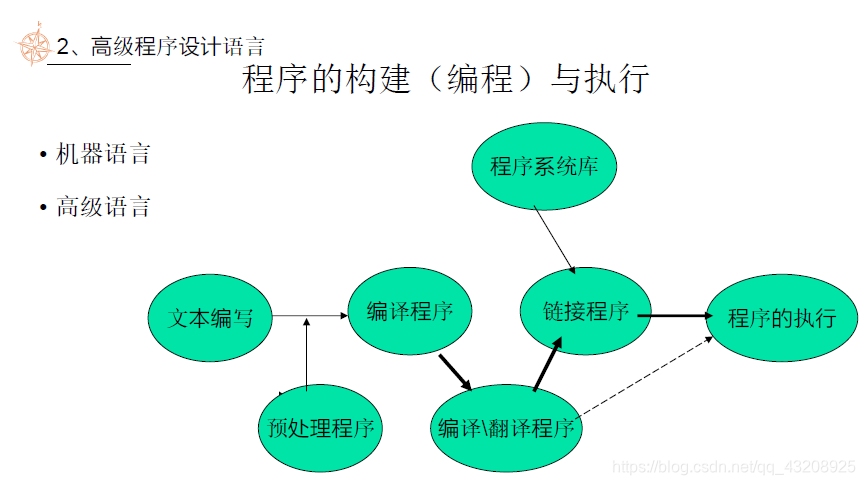
高階程式設計語言

歷史：機器語言——組合語言——高階語言

程式規劃與設計的五個步驟

1.分析問題並制定概要設計方案。準確瞭解、用準確的語言描述問題。
2.制定詳細設計。（演算法設計）精確的步驟，明確、詳細、有限、在合理時間內完成，選定語言。
3.用程式語言編寫程式程式碼和文件。需要加上註釋。
4.測試程式。確保執行正確。前幾步中不斷重複。每部分都要測試。
5.驗證程式。大範圍測試，根據使用者需要，不斷修改調整，直到使用者滿意。

軟體工程

在大型的軟體開發中，引入工程管理的一整套的管理方法，對軟體開發過程進行規劃、設計、監控和檢測，以確保開發的過程、開發時間和軟體質量都在人的控制管理之下，從而使軟體開發的順利進行。

程式設計理論

通過對程式設計的各種問題進行了系統研究，進行了規範總結。
自頂向下逐步求精
自底向上的程式設計方法

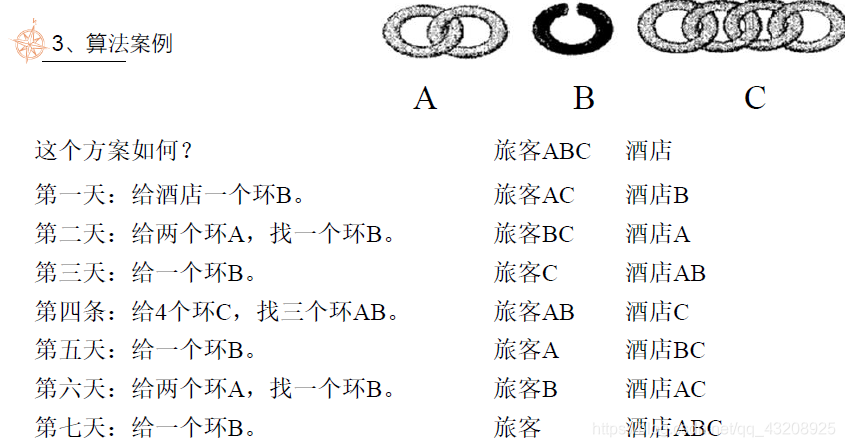
演算法案例，拓展一下腦洞

一個拿著7個金環組成的鏈子的旅行者需要在一個酒店裡住7夜。每一夜的租金是金鍊中的一環。應該如何對鏈子進行最少次數的切割，使旅行者每天早上支付酒店的一環而不用提前支付旅費？
最優解：切一次