機器學習 --- 支援向量機的核函式

阿新 • • 發佈：2018-11-24

一、核函式方法的直觀理解

線性向量機地分類效果可能並不是很好，難以分類非線性的問題，這就將引入核函式。

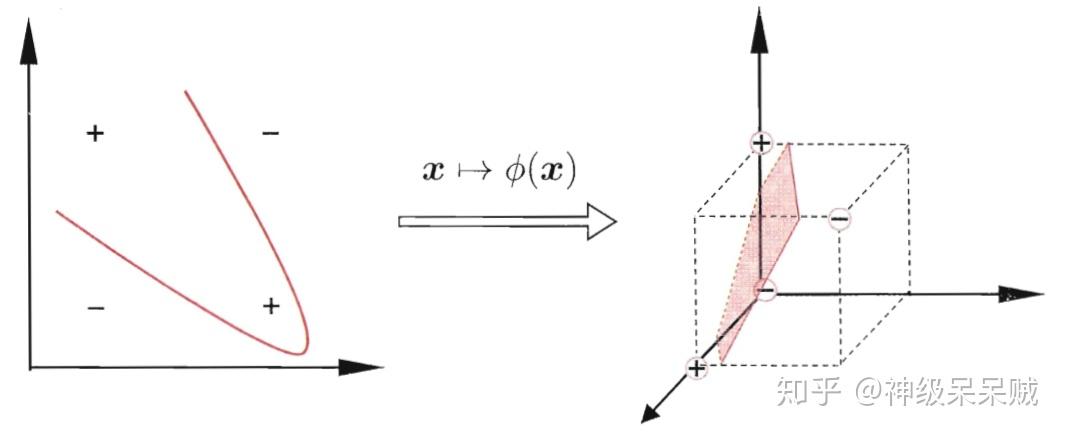
例如在二維平面中，難以通過線性的方法來處理異或問題，但是通過將輸入變數經過核函式 $\phi(\cdot)$ 對映到三維空間中，那麼如上圖所示的線性超平面可以完成分類。

線上性不可分的情況下，支援向量機首先在低維空間中完成計算，然後通過核函式，將樣本從原始空間對映到高維特徵空間，最終在高維特徵空間中構造出最優的劃分超平面。

因此，在高維的特徵空間劃分超平面模型表示成：

$f(x)=w^{T}\phi(x)+b$

$\phi(x)$ 表示成經過核函式將 $x$ 對映後的特徵向量。

二、求解帶核函式的支援向量機

由之前線性支援向量機的推導，可以得到：

$f(x)=w^{T}\phi(x)+b$

$\ \ \ \ \ \ \ \ =\sum_{i=1}^{m}{\alpha_{i}y_{i}\phi(x_{i})^T\phi(x)+b}$

$\ \ \ \ \ \ \ \ =\sum_{i=1}^{m}{\alpha_{i}y_{i}\kappa(x,x_{i})+b}$

由線性向量機的知識，推出帶核函式的規劃方程：

$\min \limits_{w,b} \frac{1}{2}\left| \left| w \right| \right|^{2}$

$s.t \quad y_{i}(w^{T}\phi(x_{i})+b)\geq1$

同樣的，其對偶問題：

$\max \limits_{\alpha} \ \sum_{i=1}^{m}{\alpha_{i}}-\frac{1}{2}\sum_{i=1}^{m}{\sum_{j=1}^{m}{\alpha_{i}\alpha_{j}y_{i}y_{j}\phi(x_{i})^{T}\phi(x_{j})}} \qquad \qquad (1)$

$s.t \ \ \ \ \sum_{i=1}^{m}{a_{i}y_{i}}=0$

$\ \quad \ \ \ \ \ a_{i}\geq0$

定義 $\kappa(x_{i},x_{j})=\phi(x_{i})^T\phi(x_{j})=<\phi(x_{i}),\phi(x)>$ ，(1)式重寫成：

$\max \limits_{\alpha} \ \sum_{i=1}^{m}{\alpha_{i}}-\frac{1}{2}\sum_{i=1}^{m}{\sum_{j=1}^{m}{\alpha_{i}\alpha_{j}y_{i}y_{j}\kappa(x_{i},x_{j})}} \qquad \qquad (2)$

$s.t \ \ \ \ \sum_{i=1}^{m}{a_{i}y_{i}}=0$

$\ \quad \ \ \ \ \ a_{i}\geq0$

使用拉格朗日乘子法求解出 $\alpha$ 後就能得到引數 $w,b$

三、核函式

如果一個對稱函式所對應的核矩陣 $K$ 半正定，它就能作為核函式使用。使用核函式做特徵對映可能隱式地定義了特徵空間，因此選取合適的核函式很重要，下面列舉一些常用的核函式。

1.高斯核函式

$\kappa(x_i,x_j)=exp(-\frac{\left| \left| x_i-x_j \right| \right|^2}{2\sigma^{2}}) \ \ \ \ \ \sigma>0$

高斯核函式可以將資料從低維對映至高維甚至無窮維。是最常用的核函式之一。

三維空間中，選取不同的 $\sigma$ 獲得不同的影象

$\sigma=1$ ：

$\sigma=5$ ：

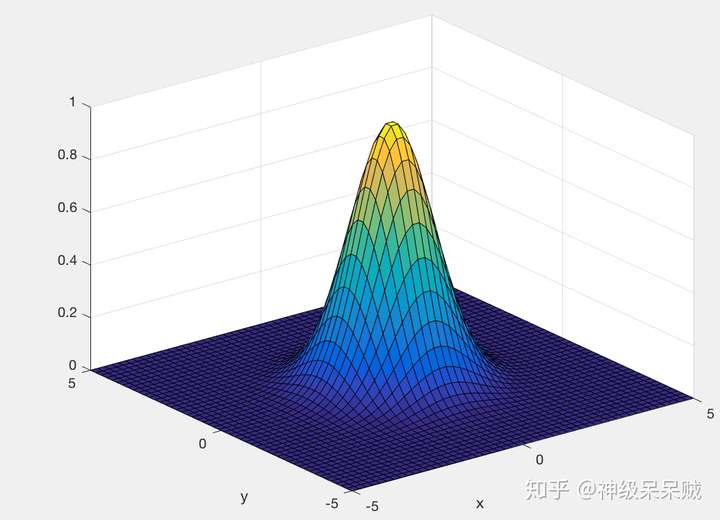
通過調節 $\sigma$ 可以獲得很高的靈活性，當 $\sigma$ 選取過大，高次特徵權重衰減得很快，因此就相當於一個低維子空間，可能會帶來高偏差，低方差的現象，反之，高次特徵權重衰減得緩慢，可將任意的資料對映為線性可分，可能會帶來低偏差，高方差的現象。

2.線性核

$\kappa(x_i,x_j)=x_i^Tx_j$

3.多項式核

$\kappa(x_i,x_j)=(x_i^Tx_j)^d \ \ \ \ \ d\geq 1$

4.拉普拉斯核

$\kappa(x_i,x_j)=exp(-\frac{\left| \left| x_i-x_j \right| \right|}{\sigma}) \ \ \ \ \ \sigma>0$

5.Sigmoid核

$\kappa(x_i,x_j)=tanh(\beta x_i^Tx_j+\theta) \ \ \ \ \ \beta>0,\theta<0$

還可以通過函式組合得到：

若 $\kappa_1, \kappa_1$ 為核函式，對於任意的正數 $\gamma_1,\gamma_2$ ，其線性組合： $\gamma_1\kappa_1+\gamma_2\kappa_2$ 也是核函式
若 $\kappa_1, \kappa_1$ 為核函式，函式的笛卡兒積： $\kappa_1\otimes \kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z)$ 也是核函式
若 $\kappa_1$ 為核函式，對於任意的函式 $g(x)$ ， $\kappa(x,z)=g(x)\kappa_1(x,z)g(z)$ 也是核函式

參考文獻：

1.支援向量機通俗導論（理解SVM的三層境界） - Mac Track - CSDN部落格

2.拉格朗日對偶問題（Lagrange duality）

3.深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT條件

4.周志華. 機器學習[M]. 清華大學出版社, 2016

5.Andrew Ng 《machine learning》系列課程

機器學習 --- 支援向量機的核函式

一、核函式方法的直觀理解線性向量機地分類效果可能並不是很好，難以分類非線性的問題，這就將引入核函式。例如在二維平面中，難以通過線性的方法來處理異或問題，但是通過將輸入變數經過核函式對映到三維空間中，那麼如上圖所示的線性超平面可以完成分類。線上性不

機器學習---支援向量機實戰（四）核函式實現

這節和上一節很像，不同的是，上一篇的是通過支援向量和待分類資料內積進行分類的，只是這裡不同的是，在計算內積時使用核函式進行代替，這裡參考的是機器學習實戰中的核函式，如果前面理解的比較深入，讀程式碼還是很簡單的，這裡的程式碼建議不要剛開始就去讀核函式定義，建議先從測試核函式的程

機器學習--支援向量機（六）徑向基核函式（RBF）詳解

前面講解了什麼是核函式，以及有效核函式的要求，到這裡基本上就結束了，很多部落格也是如此，但是呢這些只是理解支援向量機的原理，如何使用它講解的卻很少，尤其是如何選擇核函式更沒有人講，不講也是有原因的，因為核函式的選擇沒有統一的定論，這需要使用人根據不同場合或者不同問題選擇核函式

機器學習----支援向量機（核函式）

#線性不可分我們的SVM是找到一條分割直線，但是如果線性不可分怎麼辦？如下圖：可以看出，是有一個明顯的分割線的，但是不是直線，這種情況下我們怎麼用SVM呢？我們可以找到一種變化，讓變換後的資料線性可分，用圖形象的表示為：圖中的ϕ就是我們

機器學習--支援向量機（五）核函式詳解

前面我們曾經引入二維資料的非線性的情況，但是那種非線性（並不是真正意義上的非線性）是通過鬆弛因子進行優化的，如果資料比之前還複雜怎麼辦呢？複雜到即使你怎麼調節C你都無法進行分類，這個時候怎麼辦？如下例子：這個無論你怎麼調節引數都無法在二維平面內進行線性分離了，但是

機器學習——支援向量機SVM之核函式

1、在現實任務中，原始樣本空間也許不存在一個能正確劃分兩類樣本的超平面，雖然“軟間隔”概念的引入在一定程度上緩解了該問題，但是當樣本分佈的非線性程度很高的時候，“軟間隔”也無法解決這一問題 2、對於這類問題，SVM的處理方法是選擇一個核函式，其通過將資料對映到更高維

吳恩達機器學習 - 支援向量機(SVM) 吳恩達機器學習 - 支援向量機(SVM)

原吳恩達機器學習 - 支援向量機(SVM) 2018年06月24日 14:40:42 離殤灬孤狼閱讀數：218 更多

機器學習-支援向量機SVM

簡介：支援向量機（SVM）是一種二分類的監督學習模型，他的基本模型是定義在特徵空間上的間隔最大的線性模型。他與感知機的區別是，感知機只要找到可以將資料正確劃分的超平面即可，而SVM需要找到間隔最大的超平面將資料劃分開。所以感知機的超平面可以有無數個，但是SVM的超平面只有一個。此外，SVM在引入核函式之後

機器學習-支援向量機（SVM）演算法學習筆記

假設有訓練集D={(x1, y1), (x2, y2), ..., (xm, ym)}，yi{-1, 1}，分類學習最基本的想法就是基於訓練集D在樣本空間中找到一個劃分超平面，將不同類別的樣本分開。

機器學習——支援向量機SVM（一）

在之前做數學建模的時候就有使用過支援向量機的有關知識，但是對於支援向量機的理解一直不是很深刻，尤其是數學推導部分還是存在一些問題。在最近看周志華西瓜書的過程中同樣發現這一問題，西瓜書中對支援向量機的講解部分不是很詳細，所以我又查找了其他的資料。支援向量機是一種原創性（非組

機器學習——支援向量機（SVM）

本文主要參考吳恩達《機器學習》課程，以及網上各個大牛們的博文。支援向量機，是一種對線性和非線性資料進行分類的方法。它按以下方法工作：使用一種非線性對映，把原訓練資料對映到較高的維上，在新的維上，它搜尋最佳分離超平面。使用到足夠高維上的、合適的非線性對映，兩個類的資料總可以

機器學習 - 支援向量機（SVM）目錄索引

SVM目錄索引線性可分 SVM：硬間隔最大化線性 SVM：軟間隔最大化非線性 SVM：核技巧序列最小最優化演算法 (SMO）特點優點：

機器學習-支援向量機

前言 – 在前面的分類問題中，學到了線性迴歸演算法、Logistic迴歸演算法，以及決策樹中迴歸演算法，我們在資料集中通過訓練資料得到一個很好的擬合數據的模型，在圖中表現為可以找到一條直線來將正反例資料很好的分割開來，例如下圖所示：在圖中的資料集中我們可

機器學習----支援向量機（軟間隔與正則化）

Soft Margin 前面的假設一直都是線性可分，可是如果對所有樣本不能線性可分（比如有noisy）怎麼辦？或者過擬合怎麼辦？緩解該問題的一個方法就是允許支援向量機在一些樣本上出錯，為此引入軟間隔(soft margin)這個概念。即允許在一些樣本

機器學習--支援向量機通俗導論（理解SVM的三層境界）

支援向量機通俗導論（理解SVM的三層境界）作者：July 。致謝：pluskid、白石、JerryLead。說明：本文最初寫於2012年6月，而後不斷反反覆覆修改&優化，修改次數達上百次，最後修改於2016年11月。前言

機器學習——支援向量機SVM之軟間隔與正則化

1、在SVM基本型的討論中，我們一直假定樣本在樣本空間或特徵空間中是線性可分的，即存在一個超平面能將不同類的樣本完全劃分開 2、然而現實任務中往往很難確定合適的核函式使得訓練樣本在特徵空間中線性可分，即使恰好找到某個核函式使訓練集樣本在特徵空間中線性可分，也很難判斷是否

機器學習——支援向量機SVM（Support Vector Machine）（下）

1、SVM演算法特徵（1）訓練好的模型的演算法複雜度是由支援向量的個數決定的，而不是由資料的維度決定。所以，SVM不太容易產生overfitting。（2）SVM訓練出來的模型完全依賴於支援向量（

Stanford機器學習---支援向量機SVM

本欄目（Machine learning）包括單引數的線性迴歸、多引數的線性迴歸、Octave Tutorial、Logistic Regression、Regularization、神經網路、機器學習系統設計、SVM（Support Vector Machines 支

機器學習——支援向量機(SVM)

支援向量機原理支援向量機要解決的問題其實就是尋求最優分類邊界。且最大化支援向量間距，用直線或者平面，分隔分隔超平面。基於核函式的升維變換通過名為核函式的特徵變換，增加新的特徵，使得低維度空間中的線性不可分問題變為高維度空間中的線性可分問題。線性核函式：linear，不通

演算法學習——支援向量機SVM

SVM現在的公式推導很多，都是現成的，而且寫的也很好，我會提供相關資源，這篇博文主要從思想理解的方面做一個簡單介紹。 1、SVM 是如何工作的？支援向量機的基礎概念可以通過一個簡單的例子來解釋。讓我們想象兩個類別：紅色和藍色，我們的資料有兩個特徵：x 和 y。我們想要一個分類器，給定一