傳送門：http://poj.org/problem?id=3565

Description

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

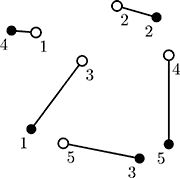
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

5
-42 58
44 86
7 28
99 34
-13 -59
-47 -44
86 74
68 -75
-68 60
99 -60

Sample Output

4
2
1
5
3

Source

題意概括：

給出 N 個螞蟻的座標 ( x1, y1 ), N 個蘋果樹的座標 ( x2, y2 )，將螞蟻和蘋果樹兩兩配對，但是路徑不能相交。

按順序輸出 第 i 個螞蟻匹配到第幾棵蘋果樹。

解題思路：

最小權值匹配的應用：做小權值匹配就保證了兩兩不相交，為什麼呢？

這是因為如果最小權匹配有兩條線段相交，那麼一定可以轉化為兩條不相交且總長度更短的兩條線段（三角形斜邊一定小於另外兩邊之和嘛），這與最小權矛盾，所以可以證明最小權匹配中沒有相交的線段。

AC code：

  1 #include <cstdio>
  2 #include <iostream>
  3 #include <algorithm>
  4 #include <cstring>
  5 #include <cmath>
  6 using namespace std;
  7 const int MAXN = 110;
  8 const double INF = 0x3f3f3f3f;
  9 struct date
 10 {
 11     double x, y;
 12 }node1[MAXN], node2[MAXN];
 13 
 14 double a[MAXN][MAXN];  //二分圖；
 15 double ex[MAXN], ey[MAXN];
 16 int linker[MAXN];
 17 bool visx[MAXN], visy[MAXN];
 18 double slack[MAXN];
 19 int N;
 20 
 21 bool Find(int x)
 22 {
 23     visx[x] = true;
 24     for(int y = 1; y <= N; y++){
 25         if(visy[y]) continue;
 26         double t = ex[x] + ey[y] - a[x][y];
 27         if(t < 1e-4){
 28             visy[y] = true;
 29             if(linker[y] == -1 || Find(linker[y])){
 30                 linker[y] = x;
 31                 return true;
 32             }
 33         }
 34         else
 35         {
 36             slack[y] = min(slack[y], t);
 37         }
 38     }
 39     return false;
 40 }
 41 
 42 void KM()
 43 {
 44     ///初始化
 45     memset(linker, -1, sizeof(linker));
 46     memset(ey, 0, sizeof(ey));
 47 
 48     for(int i = 1; i <= N; i++){
 49         ex[i] = a[i][1];
 50         for(int j = 2; j <= N; j++){
 51             ex[i] = max(ex[i], a[i][j]);
 52         }
 53     }
 54 
 55     for(int x = 1; x <= N; x++){
 56 
 57         fill(slack, slack+1+N, INF);
 58 
 59         while(1){
 60             memset(visx, 0, sizeof(visx));
 61             memset(visy, 0, sizeof(visy));
 62             if(Find(x)) break;
 63             double min_slack = INF;
 64             for(int i = 1; i <= N; i++){
 65                 if(!visy[i])
 66                     min_slack = min(min_slack, slack[i]);
 67             }
 68             for(int i = 1; i <= N; i++){
 69                 if(visx[i]) ex[i]-=min_slack;
 70             }
 71             for(int j = 1; j <= N; j++){
 72                 if(visy[j]) ey[j]+=min_slack;
 73             }
 74         }
 75     }
 76 }
 77 
 78 //double dis(date n1, date n2)
 79 //{
 80 //    double res = 0;
 81 //    res = sqrt((n1.x - n2.x)*(n1.x - n2.x) + (n1.y - n2.y)*(n1.y - n2.y));
 82 //    return -res;
 83 //}
 84 
 85 
 86 int main()
 87 {
 88     while(~scanf("%d", &N)){
 89 //        init();
 90         for(int i = 1; i <= N; i++){
 91             scanf("%lf%lf", &node1[i].x, &node1[i].y);
 92         }
 93         for(int i = 1; i <= N; i++){
 94             scanf("%lf%lf", &node2[i].x, &node2[i].y);
 95         }
 96         for(int i = 1; i <= N; i++)
 97         for(int j = 1; j <= N; j++){
 98             a[j][i] = -sqrt((node1[i].x - node2[j].x)*(node1[i].x - node2[j].x) + (node1[i].y - node2[j].y)*(node1[i].y - node2[j].y));
 99         }
100         KM();
101         for(int i = 1; i <= N; i++){
102             printf("%d\n", linker[i]);
103         }
104     }
105     return 0;
106 }