平衡樹是一個很神奇的資料結構

noip前，學了其兩種實現方式，Splay和Treap，非常實用（雖然碼量有點。。）

每個平衡樹都是二叉查詢樹，保證\(左孩子 \leq 自己 \leq 右孩子\)

因此，平衡樹的中序遍歷就是插入節點的有序序列（理解一下）

平衡樹支援插入，刪除，以及各種查詢，以下面為例

\(\color{#0066ff}{題目描述}\)

您需要寫一種資料結構，來維護一些數，其中需要提供以下操作：

插入數x

刪除x數x(若有多個相同的數，只刪除一個)
查詢數x的排名(排名定義為比當前數小的數的個數+1。若有多個相同的數，輸出最小的排名)

查詢排名為x的數

求x的前驅(前驅定義為小於x，且最大的數)

求x的後繼(後繼定義為大於x，且最小的數)

\(\color{#0066ff}{輸入格式}\)

第一行為n，表示操作的個數,下面nn行每行有兩個數opt和x，opt表示操作的序號\(1\leq opt \leq 6\)

\(\color{#0066ff}{輸出格式}\)

對於操作3,4,5,6每行輸出一個數，表示對應答案

\(\color{#0066ff}{輸入樣例}\)

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
 

\(\color{#0066ff}{輸出樣例}\)

106465
84185
492737

這就是洛谷P3369普通平衡樹板子

總的來說，平衡樹的實現方式有6種：SBT，Splay，Treap，AVL，RBT，替罪羊

其實還有一個是普通的二叉查詢樹：BST，由於太過辣雞。。。很容易被卡，此處不提

對於AVL，實用性比較低，比如程式碼長度，精簡度不如SBT，速度倒是差不多，對大資料的處理不如RBT，對可持久化的支援又不如FAQ，靈活性又沒有Splay高，還不能像替罪羊樹那樣支援樹套樹，此處也不提了

那麼，這些平衡樹根BST有啥區別呢，為什麼平衡樹要比BST快好多好多呢？

試想一下，當插入的節點使樹變成一條鏈時，每次查詢最壞豈不是\(O(n)\)

？ 顯然TLE。。。

這些平衡樹，各有各的長處，每一個都有騷操作使自己平衡，防止複雜度過高

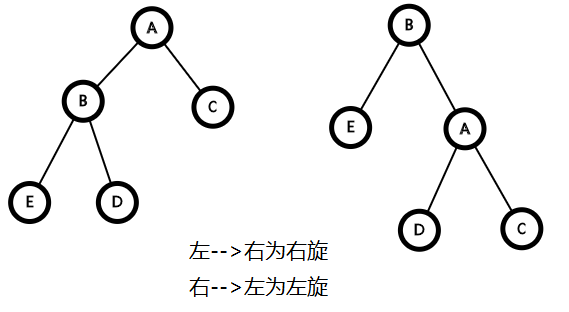
大部分平衡樹要依靠旋轉（除了Treap，替罪羊）

這裡，把旋轉提一下

剛剛說，平衡樹的\(左孩子 \leq 自己 \leq 右孩子\)

因此上圖中\(E < B < D < A < C\)

兩個根A，B互轉，D作為[A,B]內的一個元素，必須要保證它的位置（如圖）

這就是一般平衡樹的旋轉操作

接下來，會依次介紹Treap，Splay，替罪羊樹，SBT，RBT

下一篇：平衡樹學習筆記（2）-------Treap