Splay

上一篇：平衡樹學習筆記（2）-------Treap

Splay是一個實用而且靈活性很強的平衡樹

效率上也比較客觀，但是一定要一次性寫對

debug可能不是那麼容易

Splay作為平衡樹，它的平衡方式就是旋轉

暴力旋轉，赤裸裸的旋轉，各種旋轉

就是依靠玄學的旋轉來保證自己的複雜度

不廢話，上主題

\(\color{#9900ff}{定義}\)

struct node
{
    node *fa,*ch[2];
    int val,num,siz;
    node() {val=num=siz=0;}
    inline void clr() {val=num=siz=0;}
    inline bool isr() {return this==fa->ch[1];}
    inline void upd() {siz=ch[0]->siz+ch[1]->siz+num;}
};
 

siz為子樹大小，val為點權，num為點的個數（重複數字存在一個點上）

clr 清空節點，isr 判斷是否為自己父親的右孩子

\(\color{#9900ff}{基本操作}\)

1、rotate

其實這個就是第一節說的旋轉

rot(x)代表把x轉到它父親的位置上去

這也是Splay維護平衡的基礎

下面是重點了！！

把x轉到它父親y上

以下程式碼中字母對應，其中那個R是程式碼中的w（因為為中間量，要特殊對待）

inline void rot(nod x)
{
    nod y=x->fa,z=y->fa; 
    //找到y，z（注意，x轉上去後，z的孩子變成x，所以要涉及到z）
    int k=x->isr(); nod w=x->ch[!k];
    //isr是bool型的，看看是不是自己父親的右孩子，這個旋轉針對的是所有情況，不僅僅是上圖的情況
    if(y!=root) z->ch[y->isr()]=x;
    else root=x;
    //x轉上去，就要考慮y是不是根的問題
    //如果y是根，x轉上去後，自然成為了根
    //如果不是根，就要讓x替換y的位置，原來y是z的哪個孩子，現在x就是z的哪個孩子
    x->ch[!k]=y;
    y->ch[k]=w;
    //該認孩子的認孩子
    w->fa=y,y->fa=x,x->fa=z;
    //該認父親的認父親
    y->upd(),x->upd();
    //因為x在y的上一層，x的upd要基於y，所以y先來
}
 

以上部分一定要理解透徹！！！

2、Splay

這個操作使基於rotate的

Splay（x），作用是把x轉到根節點的位置上

顯然要轉好多次的qwq

因為一些玄學的東西（霧

平衡樹中，每次用到誰轉誰（反正不影響性質，說白了貌似還是瞎轉）

這樣玄學的操作可以使Splay平衡

inline void splay(nod x)
{   
    while(x!=root)
    {
        if(x->fa!=root) rot(x->isr()^x->fa->isr()? x:x->fa);
        rot(x);
    }
}
 

上面if那一行是啥意思呢？

我們要考慮一條鏈的情況

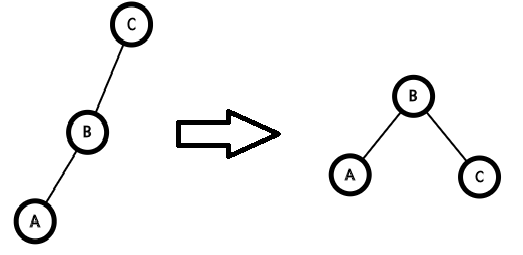
這種情況我們要先轉父親，再轉自己

否則直接轉自己就行

至此，基本操作已經結束qwq

\(\color{#9900ff}{其它操作}\)

1、插入

這個是真的暴力插。。。。。。

inline void ins(int x)
{
    if(root==null)    
    {
        //空樹則對根節點操作
        root=newnode();
        root->siz=root->num=1;
        root->val=x;
        return;
    }
    //從根開始暴力插♂
    nod fa=null;
    nod o=root;
    while(1)
    {
        if(o->val==x)
        {
            //剛剛說重複的節點存在一起，這就是重複的情況
            o->num++;
            //玄學操作，轉上去
            splay(o);
            return;
        }
        //一直往下跳（注意方向）
        fa=o;
        o=o->ch[x>o->val];
        if(o==null)
        {
            //跳到了空節點上，那麼申請新節點
            fa->ch[x>fa->val]=o=newnode();
            //千萬不要忘記父子互認
            o->fa=fa;
            o->num=o->siz=1;
            o->val=x;
            splay(o);
            return;
        }
    }
}

2、刪除

這個有點。。鬼畜

一般來說，（我所知道的）有兩種刪除方式，某崔性男子說可以merge（霧

第一種一般在陣列版寫

找到要刪節點的前驅和後繼

前驅轉到根，後繼轉到根的右孩子

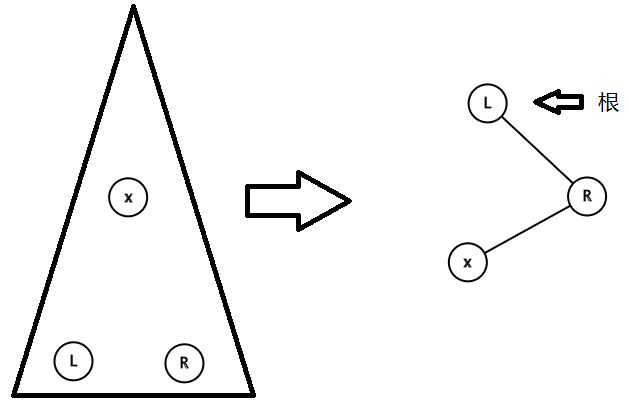
R的左子樹一定是我們要刪的，直接刪就行了（父子不互認，其他變數清空）

第二種就是我在指標寫的

需要兩個函式（好像有點麻煩吧qwq）

inline nod lst()
{
    nod o=root->ch[0];
    while(o->ch[1]!=null) o=o->ch[1];
    return o; 
}

返回根的前驅

下面的是真正的刪除

首先把要刪的節點轉到根並記錄一下

找到根的前驅

把根的前驅轉到根

那麼一定是這種情況

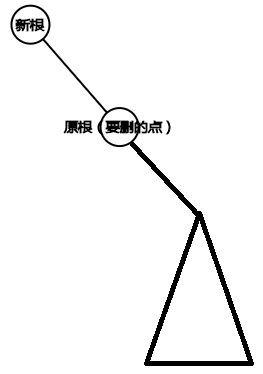
原根，也就是要刪的點，一定是沒有左孩子的！！！！

所以類似於連結串列的操作，把該刪的刪掉

inline void del(int x)
{
    rnk(x);
    //刪一個，還有
    if(root->num>=2) {root->num--; root->upd(); return;}
    //刪一個不夠了
    nod l=lst(),rt=root;
    splay(l);
    //類似於連結串列的操作，使得被刪點隔絕於此樹之外
    l->ch[1]=rt->ch[1];
    l->ch[1]->fa=l;
    rt->clr();
    l->upd();
    //清空與維護
}

3、查詢數x的排名

暴力找

inline int rnk(int x)
{
    //rank來記錄排名
    //從根開始暴力求
    int rank=0;
    nod o=root;
    while(1)
    {
        //應該往左跳
        if(o->ch[0]!=null&&x<o->val) o=o->ch[0];
        else
        {
            //到這裡說明左子樹所有點的值都<x，所以統計
            rank+=o->ch[0]->siz;
            //剛好等於
            if(x==o->val)
            {
                splay(o);
                //因為初始插了個極小值極大值，所以不用+1
                return rank;
            }
            //x比當前點還要大，所以+=num
            rank+=o->num;
            //往右跳
            o=o->ch[1];
        }
    }
}

4、查詢第k大的數

其實跟上面差不多

inline int kth(int x)
{
    nod o=root;
    while(1)
    {
        if(o->ch[0]!=null&&x<=o->ch[0]->siz) o=o->ch[0];
        else
        {
            int y=o->ch[0]->siz+o->num;
            if(x<=y) return o->val;
            x-=y;
            o=o->ch[1];
        }
    }
}

5、6、前驅，後繼

這兩個為什麼一塊寫?

因為他們幾乎一樣

inline int pre(nod o,int x)
{
    if(o==null) return -0x7fffffff;
    if(x>o->val) return nmr::max(o->val,pre(o->ch[1],x));
    //當前點成立，但遞迴下去可能不成立了，所以去max
    else return pre(o->ch[0],x);
    //當前點本來就不成立，直接遞迴
}
inline int nxt(nod o,int x)
{    
    //同上
    if(o==null) return 0x7fffffff;
    if(x<o->val) return nmr::min(o->val,nxt(o->ch[0],x));
    else return nxt(o->ch[1],x);
}

至此，Splay完

其實只要理解了，並不是想象那麼難的

放一下完整程式碼

#include<cstdio>
#include<queue>
#include<vector>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cctype>
#define _ 0
#define LL long long
#define Space putchar(' ')
#define Enter putchar('\n')
#define fuu(x,y,z) for(int x=(y);x<=(z);x++)
#define fu(x,y,z)  for(int x=(y);x<(z);x++)
#define fdd(x,y,z) for(int x=(y);x>=(z);x--)
#define fd(x,y,z)  for(int x=(y);x>(z);x--)
#define mem(x,y)   memset(x,y,sizeof(x))
template<typename T>inline void in(T &x)
{
    char ch;x=0;
    int f=1;
    while(!isdigit(ch=getchar()))f=ch=='-'? -f:f;
    while(isdigit(ch)) x=(x*10)+(ch^48),ch=getchar();
    x*=f;
}
template<typename T>inline void out(T x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) out(x/10);
    putchar(x%10+'0');
}
namespace nmr
{
    template<typename T>inline  T abs(T a) {return a>0? a:-a;}
    template<typename T>inline void swap(T &a,T &b) {T t=a; a=b; b=t;}
    template<typename T>inline const T &min(const T &a,const T &b) {return a>b? b:a;}
    template<typename T>inline const T &max(const T &a,const T &b) {return a>b? a:b;}
}
int n,cnt;
struct node
{
    node *fa,*ch[2];
    int val,num,siz;
    node() {val=num=siz=0;}
    inline void clr() {val=num=siz=0;}
    inline bool isr() {return this==fa->ch[1];}
    inline void upd() {siz=ch[0]->siz+ch[1]->siz+num;}
};
typedef node* nod;
node st[123456];
nod root,null;
inline nod newnode()
{
    cnt++;
    st[cnt].fa=st[cnt].ch[1]=st[cnt].ch[0]=null;
    return &st[cnt];
}
inline void rot(nod x)
{
    nod y=x->fa,z=y->fa; 
    int k=x->isr(); nod w=x->ch[!k];
    if(y!=root) z->ch[y->isr()]=x;
    else root=x;
    x->ch[!k]=y;
    y->ch[k]=w;
    w->fa=y,y->fa=x,x->fa=z;
    y->upd(),x->upd();
}
inline void splay(nod x)
{   
    while(x!=root)
    {
        if(x->fa!=root) rot(x->isr()^x->fa->isr()? x:x->fa);
        rot(x);
    }
}
inline int rnk(int x)
{
    int rank=0;
    nod o=root;
    while(1)
    {
        if(o->ch[0]!=null&&x<o->val) o=o->ch[0];
        else
        {
            rank+=o->ch[0]->siz;
            if(x==o->val)
            {
                splay(o);
                return rank;
            }
            rank+=o->num;
            o=o->ch[1];
        }
    }
}
inline int kth(int x)
{
    nod o=root;
    while(1)
    {
        if(o->ch[0]!=null&&x<=o->ch[0]->siz) o=o->ch[0];
        else
        {
            int y=o->ch[0]->siz+o->num;
            if(x<=y) return o->val;
            x-=y;
            o=o->ch[1];
        }
    }
}
inline nod lst()
{
    nod o=root->ch[0];
    while(o->ch[1]!=null) o=o->ch[1];
    return o; 
}
inline int pre(nod o,int x)
{
    if(o==null) return -0x7fffffff;
    if(x>o->val) return nmr::max(o->val,pre(o->ch[1],x));
    else return pre(o->ch[0],x);
}
inline int nxt(nod o,int x)
{
    if(o==null) return 0x7fffffff;
    if(x<o->val) return nmr::min(o->val,nxt(o->ch[0],x));
    else return nxt(o->ch[1],x);
}
inline void ins(int x)
{
    if(root==null)
    {
        root=newnode();
        root->siz=root->num=1;
        root->val=x;
        return;
    }
    nod fa=null;
    nod o=root;
    while(1)
    {
        if(o->val==x)
        {
            o->num++;
            splay(o);
            return;
        }
        fa=o;
        o=o->ch[x>o->val];
        if(o==null)
        {
            fa->ch[x>fa->val]=o=newnode();
            o->fa=fa;
            o->num=o->siz=1;
            o->val=x;
            splay(o);
            return;
        }
    }
}
inline void del(int x)
{
    rnk(x);
    if(root->num>=2) {root->num--; root->upd(); return;}
    nod l=lst(),rt=root;
    splay(l);
    l->ch[1]=rt->ch[1];
    l->ch[1]->fa=l;
    rt->clr();
    l->upd();
}
int main()
{
    in(n);
    null=&st[0];
    null->ch[1]=null->ch[0]=null->fa=null;
    root=null;
    ins(0x7fffffff);
    ins(-0x7fffffff);
    int p,x;
    while(n--)
    {
        in(p),in(x);
        if(p==1) {ins(x);}
        if(p==2) {del(x);}
        if(p==3) {out(rnk(x));Enter;}
        if(p==4) {out(kth(x+1));Enter;}
        if(p==5) {out(pre(root,x));Enter;}
        if(p==6) {out(nxt(root,x));Enter;}
    }
    return ~~(0^_^0);
}