文章目錄

• 1. 題目描述：
• 2. 思路分析：
• 3. Java程式碼：

1. 題目描述：

Given n non-negative integers a[1], a[2], …, a[n] , where each represents a point at coordinate (i, a[i]). n vertical lines are drawn such that the two endpoints of line i is at (i, a[i]) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

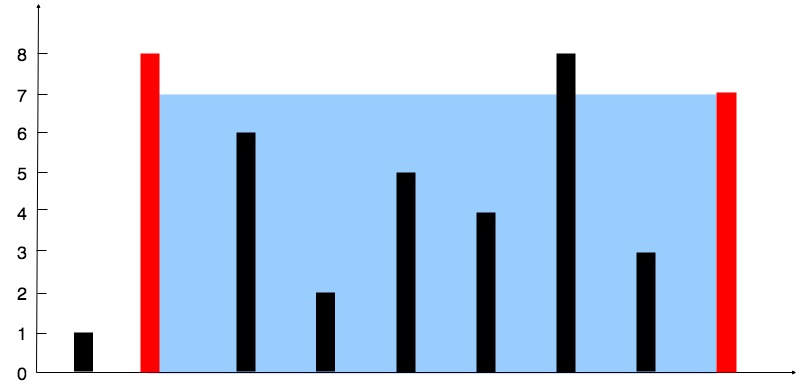
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

2. 思路分析：

題目的意思是找兩條豎線然後這兩條線以及X軸構成的容器能容納最多的水。

最簡單粗暴的方式是兩兩遍歷的雙重迴圈做法，算出所有可能情況，返回最大的。但這種方式時間複雜度是O(n^2)，太慢了。

尋求更簡單的解法的思路就是省去沒有必要的遍歷，並且確保所需的答案一定能被遍歷到。

假設現在有一個容器，則容器的盛水量取決於容器的底和容器較短的那條線，則我們可以從最長的底入手，即當容器的底等於陣列的長度時，則容器的盛水量為較短邊的長乘以底。可見 只有較短邊會對盛水量造成影響，因此移動較短邊的指標，並比較當前盛水量和當前最大盛水量。直至左右指標相遇。時間複雜度是O(n)。

主要的困惑在於如何移動雙指標才能保證最大的盛水量被遍歷到？
假設有左指標left和右指標right，且a[left] < a[right]，假如我們將右指標左移，則右指標左移後的值和左指標指向的值相比有三種情況:

• a[left] < a[right’]
  這種情況下，容器的高取決於左指標，但是底變短了，所以容器盛水量一定變小;
• a[left] == a[right’]
  這種情況下，容器的高取決於左指標，但是底變短了，所以容器盛水量一定變小;
• a[left] > a[right’]
  這種情況下，容器的高取決於右指標，但是右指標小於左指標，且底也變短了，所以容量盛水量一定變小了;

綜上所述，容器高度較大的一側的移動只會造成容器盛水量減小;所以應當移動高度較小一側的指標，並繼續遍歷，直至兩指標相遇。

3. Java程式碼：

原始碼：見我GiHub主頁

程式碼：

public static int maxArea(int[] height) {
    int maxArea = 0;
    int l = 0;
    int r = height.length - 1;
    while (l < r) {
        int curArea = Math.min(height[l], height[r]) * (r - l);
        maxArea = Math.max(maxArea, curArea);
        if (height[l] < height[r]) {
            l++;
        } else {
            r--;
        }
    }
    return maxArea;
}