購物籃演算法想必大家並不陌生，隨便翻開任何一本資料探勘的書，開篇都會講牛奶和啤酒的故事，而購物籃演算法中有一個很重要的演算法是Aprioi演算法，演算法詳解可見如下連結。

https://blog.csdn.net/baimafujinji/article/details/53456931

    在進行Aprioi演算法的頻繁項集選擇時，比較常見的一個操作是從一堆物品集合中挑選出兩兩組合或者三三組合的這些小集合，其實就類似於從一堆資料中隨機選擇幾個數，並對其進行列舉。

       舉個例子：葫蘆娃一共有"紅黃藍綠橙靛紫"七種顏色，請幫我隨機選擇兩種顏色，請問一共有多少種選擇方法，並將其枚舉出來，學過一點概率論的同學應該都清楚，這個數字應該等於7*6/（2！）=21種；那如果要隨機取三種呢，應該是7*6*5/（3！）=35種，頻繁項集的挑選中，這是非常常見的一步，那麼問題來了，怎麼來進行這個操作呢。

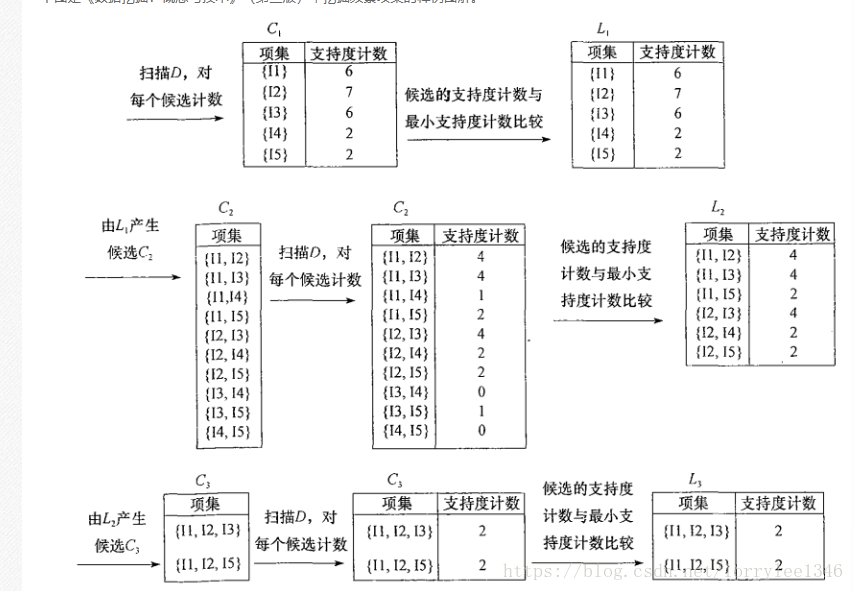
     還是需要拿這個圖來說明一下，兩個元素的集合來自於一個元素的集合，三個元素的集合又來自於兩個元素的集合，同理，四個元素的集合又來自於三個元素的集合，最終可知七個元素的集合來自於六個元素的集合並最終可以湊在一起變成葫蘆小金剛。

     對Aprioi演算法的解釋很多文章已經寫的很清楚，本文僅針對從一堆選項中形成自己想要的幾層集合所需要的函式進行說明。如果只是要寫到二項集或者三項集，完全可以寫兩個函式就可以，但你不能保證你的老闆不會讓你分析到10層或者20層，寫20個函式或者20層迴圈，想著應該是一件很蠢，並且很沒有收益的事情，還好python跟C一樣，都是可以呼叫遞迴函式，也就是說自己可以呼叫自己，多麼美妙的一件事。

話不多說，直接上程式碼。

#確定顏色集合
color= [['紅'],['橙'],['黃'],['綠'],['藍'],['靛'],['紫']]

#說明，將顏色集合設定成列表套列表的形式，主要在於二項，或者三項以列表形式存貯更為方便

#列表合併函式
def list_merge(listA):
    length = len(listA)
    listB = []        
    for i in range(0,length-1):
        a = list(listA[i])
        for j in range(i+1,length):
            b = a + list(listA[j])
            set_b = list(set(b))
            set_b.sort()
            if len(set_b) == len(a)+1 and set_b not in listB:
                listB.append(set_b)            
    
    return listB   

#遞迴函式
def create_set(listA, num):
    if num<=1:
        return listA
    else:
        return create_set(list_merge(listA), num-1)

color_result = create_set(color, num=3)
print(color_result)
##################################
[['橙', '紅', '黃'], ['橙', '紅', '綠'], ['橙', '紅', '藍'], ['橙', '紅', '靛'], ['橙', '紫', '紅'], ['紅', '綠', '黃'], ['紅', '藍', '黃'], ['紅', '靛', '黃'], ['紫', '紅', '黃'], ['紅', '綠', '藍'], ['紅', '綠', '靛'], ['紫', '紅', '綠'], ['紅', '藍', '靛'], ['紫', '紅', '藍'], ['紫', '紅', '靛'], ['橙', '綠', '黃'], ['橙', '藍', '黃'], ['橙', '靛', '黃'], ['橙', '紫', '黃'], ['橙', '綠', '藍'], ['橙', '綠', '靛'], ['橙', '紫', '綠'], ['橙', '藍', '靛'], ['橙', '紫', '藍'], ['橙', '紫', '靛'], ['綠', '藍', '黃'], ['綠', '靛', '黃'], ['紫', '綠', '黃'], ['藍', '靛', '黃'], ['紫', '藍', '黃'], ['紫', '靛', '黃'], ['綠', '藍', '靛'], ['紫', '綠', '藍'], ['紫', '綠', '靛'], ['紫', '藍', '靛']]
 

該問題的主要解決思路在於對遞迴函式的呼叫，同時在對列表函式做好排序、去重的基礎之上，確保每次只保留需要的層級，並且可作為下一步操作的輸入，在尋找頻繁項集中，可利用該函式快速有效地確定不同集合的組成，以及對應的出現次數。