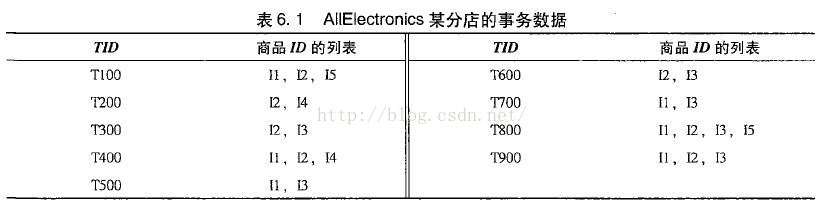
海量資料探勘MMDS week2: 頻繁項集挖掘 Apriori演算法的改進:基於hash的方法
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之關聯規則Apriori演算法的改進:基於hash的方法:PCY演算法,
Multistage演算法, Multihash演算法
Apriori演算法的改進
{All these extensions to A-Priori have the goal of minimizing the number of pairs that actually have to be counted on the second pass.}
當頻繁項對的數量比較大時,記憶體放不下,而這時對頻繁項對進行計數時,可能會產生記憶體抖動,即記憶體頁面頻繁換入換出,因為不同的頻繁項對計數器可能放在不同的頁面上。
Apriori演算法的改進演算法
這些演算法可以用在海量資料上的關聯規則挖掘中。
(1)基於hash的方法。一個高效地產生頻集的基於雜湊(hash)的演算法由Park等提出來。通過實驗可以發現尋找頻集主要的計算是在生成頻繁2-項集Lk上,Park等就是利用了這個性質引入雜湊技術來改進產生頻繁2-項集的方法。
基於雜湊的演算法仍是將所有所有資料放入記憶體的方法。只要在計算的過程中能夠滿足演算法對記憶體的大量需求,Apriori演算法能夠很好的執行。但在計算候選項集時特別是在計算候選項對C2時需要消耗大量記憶體。針對C2候選項對過大,一些演算法提出用來減少C2的大小。這裡我們首先考慮PCY演算法,這個演算法使用了在Apriori演算法的第一步裡大量沒使用的記憶體。接著,我們考慮Multistage演算法,這個演算法使用PCY的技巧,但插入了額外的步驟來更多的減少C2的大小。類似的還有Multihash。
(2)基於劃分的方法。Savasere等設計了一個基於劃分(partition)的演算法.這個演算法先把資料庫從邏輯上分成幾個互不相交的塊,每次單獨考慮一個分塊並對它生成所有的頻集,然後把產生的頻集合並,用來生成所有可能的頻集,最後計算這些項集的支援度。這裡分塊的大小選擇要使得每個分塊可以被放入主存,每個階段只需被掃描一次。而演算法的正確性是由每一個可能的頻集至少在某一個分塊中是頻集保證的。
(3)基於取樣的方法。基於前一遍掃描得到的資訊,對此仔細地作組合分析,可以得到一個改進的演算法,Mannila等先考慮了這一點,他們認為取樣是發現規則的一個有效途徑。
Apriori演算法回顧
Apriori演算法流程步驟圖解
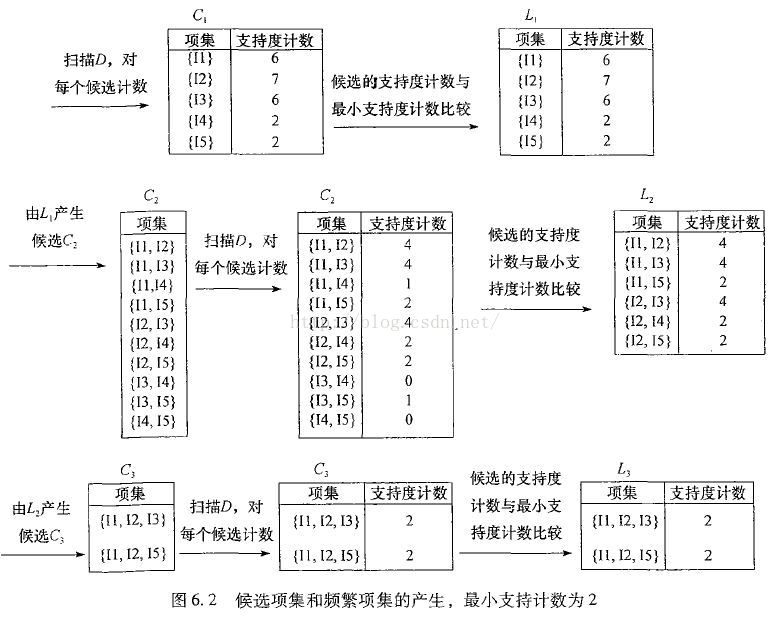
資料探勘概念與技術中對Apriori演算法的圖解
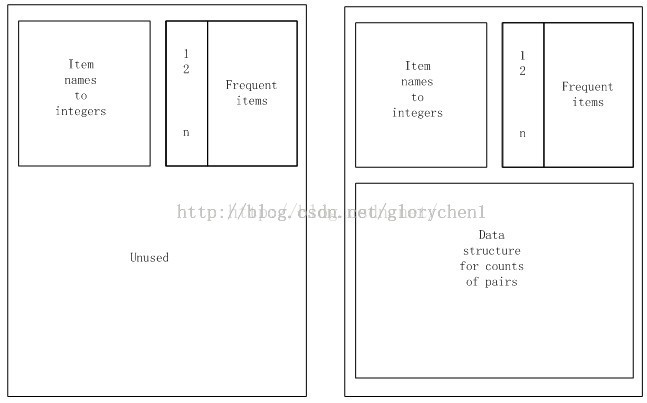
Apriori演算法的記憶體的使用情況
左邊為第一步時的記憶體情況,右圖為第二步時記憶體的使用情況
在第一步(對所有item掃描計數,並選出頻繁一項集)裡,我們只需要兩個表,一個用來儲存項的名字到一個整數的對映,用這些整數值代表項,一個數組來計數這些整數。
PCY演算法(Park-Chen-Yu algorithm)PCY演算法使用了在Apriori演算法的第一步裡大量沒使用的記憶體,該演算法關注在頻繁項集挖掘中的第一步有許多記憶體空間沒被利用的情況。如果有數以億計的項,和以G計的記憶體,在使用關聯規則的第一步裡我們將會僅僅使用不到10%的記憶體空間,會有很多記憶體空閒。
對Aprior進行改進:第一步掃描
從basket中統計項的個數用於尋找頻繁一項集,並從每個basket中產生所有項對,併為項對建立一張hash表,hash表只是統計hash到本桶的項對的個數。
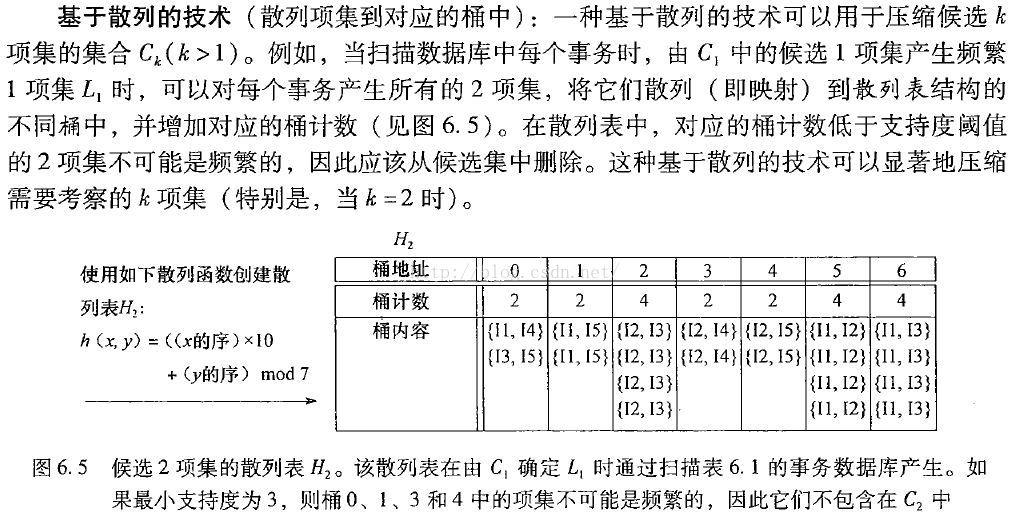
資料探勘概念與技術中對PCY演算法解釋的一個示例
1. 這一步相當於提前進行一次非頻繁項對的篩選,如果將所有不同項對hash到不同桶中,當然就相當於Apriori演算法對所有項對進行計數了,記憶體還是會超的!但是,這裡我們項對hash時會有不同的項對hash到同一個桶中,即使是多個項對,如果它們都是非頻繁的,加起來也很可能是非頻繁的(很多情況下)。刪除掉這些包含許多非頻繁項對的非頻繁桶,就篩選掉了很多完全不必進入候選二項集C2的的項對。
2. 圖中桶內容只是便於理解,實際只儲存桶計數,不儲存桶內容。
假設我們有1G的記憶體可用來在第一步做hash表存放,並假設資料檔案包含在10億籃子,每個籃子10個項。一個桶為一個整數,通常定義為4個位元組,於是我們可以儲存2.5億個桶。
所有籃子的項對的數量總數為即
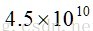
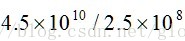
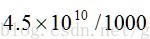
PCY演算法pass1虛擬碼
對Aprior進行改進:第二步掃描
統計哪些是頻繁桶,並只需對雜湊到頻繁桶的兩個頻繁項進行計數處理,只有頻繁桶中的項對才會當作是候選項對。這樣每個頻繁桶內的頻繁項集比較少,尋找更大頻繁項集的計算量就大大降低了。

在PCY演算法第二步操作前,雜湊表被壓縮為bitmap,在這裡,每一個bit用作一個桶。若桶為頻繁桶,則位置1,否則置0。這樣32bit的整數被壓縮為只有1bit。然後再PCY的第二步操作中,bitmap只佔了原來所用空間的1/32。
如果大部分的桶都是非頻繁桶,我們可以預料,在第二步的項對計數後產生的頻繁項集會更小。這樣,PCY演算法就能直接在記憶體中處理這些資料集而不會耗盡記憶體。
PCY中的候選集C2為這樣的項對{i, j}:
1. i和j是頻繁項
2. {i,j}雜湊到一個頻繁桶(這是PCY與Apriori的區別)
Note:1. 候選集C2中候選項對{i, j}在Apriori中的唯一條件是:i和j是頻繁項
2. When we count pairs on the second pass,we have to use the tabular method.
lz分析的pass2的演算法應該是這樣的:掃描每個basket中所有的項對,如果項對中每一項都是頻繁項(頻繁一項集),並且 {i,j}雜湊後對應到一個頻繁桶,則將這個項對加入到{item, item, count}中,組成一個Tabular Table。
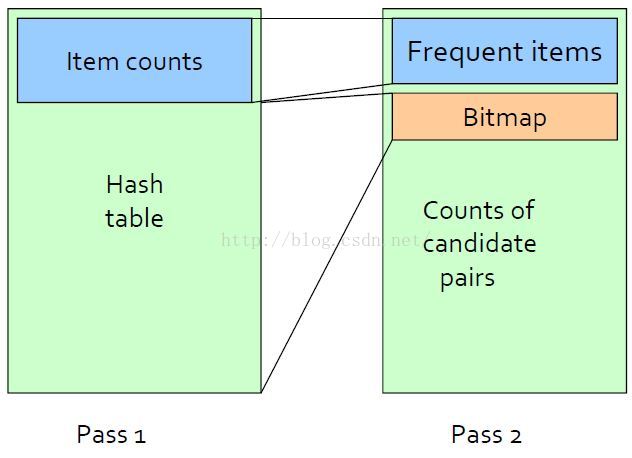
PCY演算法記憶體使用分析
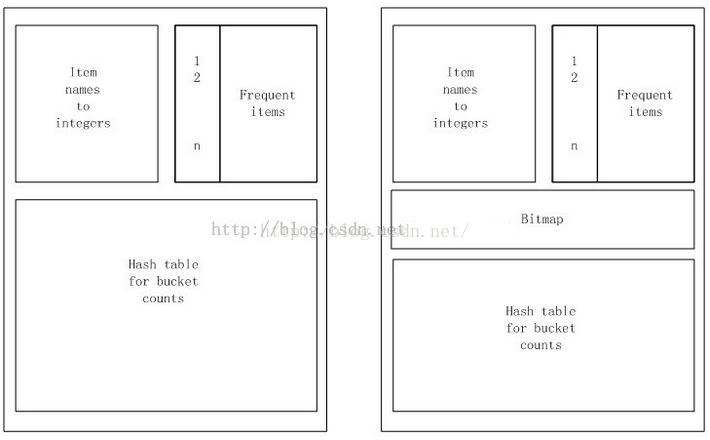
PCY演算法的記憶體組織形式,左圖為步驟1的記憶體使用情況,右圖為步驟2的記憶體使用情況
第一步記憶體使用詳解
PCY演算法使用第一步空閒的記憶體來儲存一個整數陣列。將這個陣列看做一個雜湊表,表的桶中裝的是整數值而不是一組key值。項對被雜湊到這些桶中。在第一步掃描籃子的處理中,我們不但將這些項對加一,並且通過兩步迴圈,我們創造出所有的項對。我們將項對雜湊到雜湊表中,並且將雜湊到的位置加一。注意,項本身不會進入桶,項對的加入只是影響桶中的整數值。On the first pass when we read a basket we not only increment the count for each of it's items.We also hash each pair that is contained in the basket.And for each resulting bucket,we increment it's count by one.
實際上每個bucket只需要使用2bytes來計數,因為支援度S一般不會超過2bytes大小的數,而計數等於S後沒必要再+1。In many cases we can get by with two bytes per bucket.The reason is that it is sufficient to count after this poor threshold S, What we really want to do is,if the current count is less than
S, and increment the count,otherwise leave the count at S.
第二步記憶體使用詳解

但是頻繁桶中也可能都是非頻繁項對。Even without any frequent pair, a bucket can be frequent.Because each bucket's count is the sum of the counts of all of the pairs that hash to it.
But the only time that we have to count a pair in the second pass, and that pair turns out to not to be frequent,is when the pair consists of two frequent items.
However, we get a lot of leverage when a bucket is not frequent.In that case, we do not have to count any of the pairs that count for that bucket even if that pair consist of two frequent items.
在PCY演算法第二步操作前,雜湊表被壓縮為bitmap,在這裡,每一個bit用作一個桶。若桶為頻繁桶,則位置1,否則置0。這樣32bit的整數被壓縮為只有1bit。然後再PCY的第二步操作中,bitmap只佔了原來所用空間的1/32。
如果大部分的桶都是非頻繁桶,我們可以預料,在第二步的項對計數後產生的頻繁項集會更小。這樣,PCY演算法就能直接在記憶體中處理這些資料集而不會耗盡記憶體。
使用tabular方法When we count pairs on the second pass,we have to use the tabular method.[關於triangular和tabular儲存方式參考]
The problem is that the pairs that are eliminated because they hash to an infrequent bucket, are scattered all over the place, and cannot be organized into a nice triangular array.因為riangular要確定的項對的數目,然而刪除了(bitmap對應位為0)多少個項對並不知道。
PCY演算法的取捨
1. As a result, we should not use PCY unless we can eliminate at least two-thirds of the candidate pairs when compared with A-Priori.
2. 在步驟1中使用hash表可能並不能帶來好處,這取決於資料大小和空閒記憶體大小。在最壞的情形下,所有的桶都是頻繁的,PCY計算的項對與A-priori是一樣的。然而,在通常的情況下,大多數的桶都是非頻繁的。這種情況下,PCY演算法降低了第二步記憶體的使用。也就是說,只有桶平均計數值<閾值S,則大多數桶是非頻繁的,可以刪除很多非頻繁項對,這時PCY演算法才更有效。
3. The number of buckets will be fraction of the size of main memory,typically almost half or a quarter.The only time that would not be true is if there were so many different items, that we needed all of most of main memory just to count them.In that case
we could not use the PCY algorithm.
Mutistage 演算法 多步雜湊演算法
Multistage演算法是在PCY演算法的基礎上使用一些連續的雜湊表來進一步降低候選項對。相應的,Multistage需要不止兩步來尋找頻繁項對。
我們知道,在PCY第一次遍歷後,得到的頻繁桶中也可能都是非頻繁項對。如果我們能再次對PCY的候選項對進行一次hash(使用另一種hash函式),就能進一步刪除掉候選項對中的非頻繁項對。。
Multistage演算法步驟
Multistage的第一步跟PCY的第一步相同。
在第一步後,頻繁桶集也被壓縮為bitmap,這也和PCY相同。但是在第二步,Multistage不計數候選項對。而是使用空閒主存來存放另一個雜湊表,並使用另一個雜湊函式。因為第一個雜湊表的bitmap只佔了1/32的空閒記憶體,第二個雜湊表可以使用幾乎跟第一個雜湊表一樣多的桶。
Multistage的第二步,我們同樣是需要遍歷籃子檔案。只是這步不需要再對候選項進行計數了,我們雜湊這些候選項對{i, j}到第二個雜湊表的桶中。一個候選項對{i, j}如同PCY演算法一樣,被雜湊僅當它滿足兩個條件:如果i和j都是頻繁的且它們在第一步被雜湊到頻繁桶中。這樣,第二個雜湊表中的計數總數將比第一步明顯減少,能再次對PCY的候選項對進行一次hash(使用另一種hash函式),就能進一步刪除掉候選項對中的非頻繁項對。可知即便是在第二步是由於第一步的bitmap佔據了1/32的空閒空間,剩下的空間也照樣夠第二步的hash表使用。
Multistage的第三步--計算候選頻繁項對,一開始第二個hash表同樣被壓縮成bitmap。該bitmap也同樣儲存在記憶體中。這時,兩個bitmap加起來也只佔到不到空閒記憶體的1/16,還有相當的記憶體可用來做第三步的計算候選頻繁項對的處理。
一個相對{i,j}在C2中,當且僅當滿足:
1、 i和j都是頻繁項
2、 {i,j}在第一步雜湊時被雜湊到頻繁桶中
3、 {i,j}在第二步雜湊時被雜湊到頻繁桶中
Multistage方法和PCY方法的主要區別
在於第二步pass2,PCY直接在pass2中得到候選項對,並掃描所有basket對候選項對進行計數來篩選出頻繁二項集;而Multistage將在pass2中得到候選項對再次進行hash,到pass3中再篩選出頻繁二項集。
一步中使用多個hash函式
很顯然,在演算法中可用在第一步和最後一步中新增任意多的中間步驟。這裡的限制就是在每一步中必須用一個bitmap來儲存前一步的結果,最終這裡會使得沒有足夠的記憶體來做計數。不管我們使用多少步驟,真正的頻繁項對總是被雜湊到一個頻繁桶中。If PCY gives you an average count of 1 tenth of the support threshold,then you can use five hash tables instead.
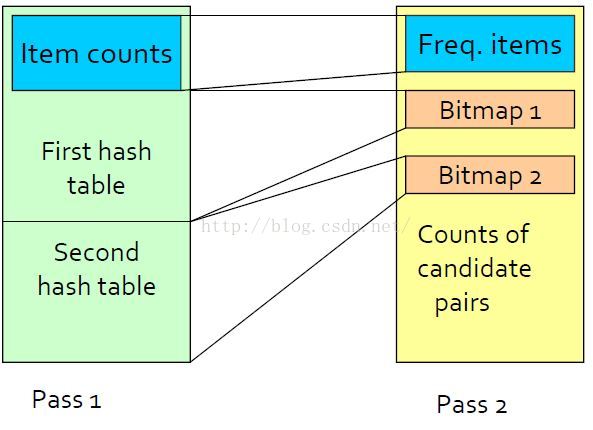
Multistage演算法圖解
Multistage演算法使用額外的雜湊表來減少候選項對,左圖為第一步記憶體使用情況,中圖為第二步記憶體使用情況,右圖為第三步記憶體使用情況
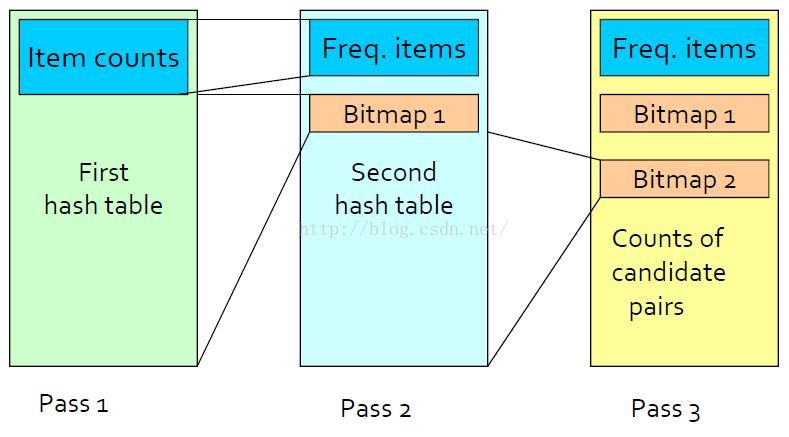
pass2中的hash table中hash的項對滿足兩個條件:i和j都是頻繁項;{i,j}在第一步雜湊時被雜湊到頻繁桶中。
pass3中的candidate pairs中項對滿足三個條件:i和j都是頻繁項; {i,j}在第一步雜湊時被雜湊到頻繁桶中; {i,j}在第二步雜湊時被雜湊到頻繁桶中。
要注意的問題
pass3中的candidate pairs中項對滿足三個條件中必須要有:i和j都是頻繁項; {i,j}在第一步雜湊時被雜湊到頻繁桶中。
因為有這種情況:i和j都是頻繁項;{i,j}在第一步雜湊時被雜湊到非頻繁桶中;{i,j}在第二步雜湊時被雜湊到頻繁桶中。(但是這個好像有問題?{i,j}在第二步雜湊時,{i,j}必須滿足在第一步雜湊時被雜湊到頻繁桶中的條件)
Multihash演算法
多次雜湊演算法
multistage演算法和Multihash演算法的區別及取捨
multistage演算法在連續的兩個步驟中使用兩個雜湊表,Multihash演算法在一步中使用兩個雜湊演算法和兩個分離的雜湊表。
在同一步裡使用兩個hash表的危險是每個雜湊表僅有PCY演算法的一半的桶, 這樣每個桶上的平均計數會翻倍,我們必須保證大多bucket不會達到閾值S。只要PCY演算法的桶的平均計數比支援度閾值低,我們就可以預見大部分的桶都是非頻繁桶,並可以在這兩個只有一半大小的雜湊表上操作完成。在這種情形下,我們選擇multihash方法。
對Multihash的第二步,每個hash表也會被轉換為一個bitmap,並且兩個bitmap佔據的空間只有PCY演算法的一個bitmap的大小。項對{i,j}被放入候選集C2的條件:i和j必須是頻繁的,且{i,j}對在兩個雜湊表中必須被hash到頻繁桶。
當然,在Multihash演算法中,我們也可以不用限制只使用兩個hash表。在Multihash演算法的第一步中,我們也可以使用多個hash表。不過風險是桶的平均計數會超過閾值,在這種情況下,這裡會只有很少的非頻繁桶在每個hash表中。即使這樣,一個項對必須被hash到每個hash表的頻繁桶中並計數,並且我們會發現,一個非頻繁項對作為一個候選的概率將上升,無利反而有害。
multistage演算法圖解
項對{i,j}被放入候選集C2的條件:i和j必須是頻繁的;{i,j}對在兩個雜湊表中都被hash到頻繁桶中。
Reviews複習
Note:
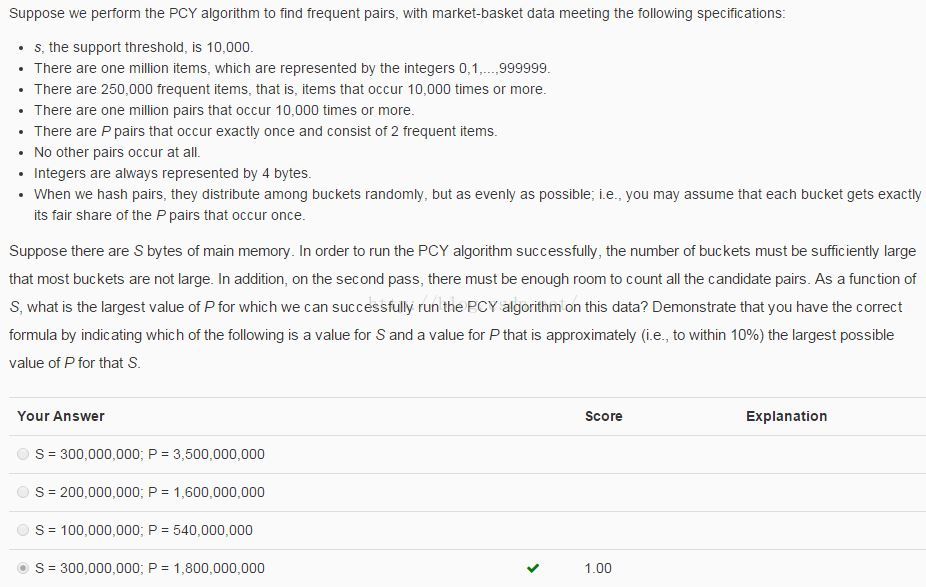
首先定義幾個變數:桶buckets的數目為B,Items的數目為I = 10^6,頻繁項對數目M = 10^6,我們要求的是P和S要滿足的關係。
第一步中的記憶體消耗:4*B + 4*I <=S,由於4個選項中S的數量級都為10^8,故可認為4*B <=S, 也就是說桶的數目S最多為B = S/4,這也是保證PCY演算法成功執行的條件(桶數目要足夠大,題目中也有說明)
第二步中的記憶體消耗:12*(P/B*M + M) <=S(Tabular方式儲存)。由於第二步的記憶體主要由候選項對消耗,而候選項對一定包含頻繁項集M個,並且也包含不是頻繁項對的項對{i, j}(就是P中的項對),其中i,j都是頻繁項,並被隨機hash到頻繁桶(由於桶數目足夠大,則頻繁桶數目有M個)中,由於是均勻隨機hash的,這樣的項對{i, j}有P/B*M個。同時可以看出P/B遠大於1,故可認為12*P/B*M <=S。
綜上,可得出不等式:P <= S^2/(5*10^7),P的最大取值為P = S^2/(5*10^7)
S = 3*10^8, P = 2*10^9選項1過大,選項4差不多
S = 2*10^8, P = 10^9選項2過大
S = 1*10^8, P = 2*10^8選項3過大
R. Agrawal, T. Imielinski, and A. Swami. Mining association rules between sets of items in large databases. Proceedings of the ACM SIGMOD Conference on Management of data, pp. 207-216, 1993.
A. Savasere, E. Omiecinski, and S. Navathe. An efficient algorithm for mining association rules in large databases. Proceedings of the 21st International Conference on Very large Database, 1995J. S. Park, M. S. Chen, and P. S. Yu. An effective hash-based algorithm for mining association rules. Proceedings of ACM SIGMOD International Conference on Management of Data, pages 175-186, San Jose, CA, May 1995.
H. Mannila, H. Toivonen, and A. Verkamo. Efficient algorithm for discovering association rules. AAAI Workshop on Knowledge Discovery in Databases, 1994, pp. 181-192.
J.Han,J.Pei,and Y.Yin.Mining frequent patterns without candidate generation.In Proc.2000 ACM-SIGMOD Int.Conf.Management of Data(SIGMOD’00),Dalas,TX,May 2000.
Edith Cohen, Mayur Datar, Shinji Fujiwara, Aristides Gionis, Piotr Indyk, Rajeev Motwani, Jeffrey D.Ullman, Cheng Yang. Finding Interesting Associations without Support Pruning. 1999
M. Fang, N. Shivakumar, H. Garcia-Molina, R. Motwani, and J. D. Ullman, “Computing iceberg queries efficiently,” Intl. Conf. on Very Large Databases, pp. 299-310, 1998.
H. Toivonen, “Sampling large databases for association rules,” Intl. Conf. on Very Large Databases, pp. 134–145, 1996.
相關推薦
海量資料探勘MMDS week2: 頻繁項集挖掘 Apriori演算法的改進:基於hash的方法
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之關聯規則Apriori演算法的改進:基於hash的方法:PCY演算法, Multistage演算法, Multihash演算法 Apriori演
海量資料探勘MMDS week2: 頻繁項集挖掘 Apriori演算法的改進:非hash方法
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之關聯規則Apriori演算法的改進:非hash方法 - 大資料集下的頻繁項集:挖掘隨機取樣演算法、SON演算法、Toivonen演算法 Apri
海量資料探勘MMDS week2: Association Rules關聯規則與頻繁項集挖掘
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記之association rules關聯規則與頻繁項集挖掘 {Frequent Itemsets: Often called "associatio
資料探勘---頻繁項集挖掘Apriori演算法的C++實現
1 準備 2 作業粗糙翻譯內容 2.1 前言 程式設計作業可能比書面作業花費更多的時間,而這也算是你最後成績的10%,所以請提前開始; 這是個人作業,你可以與你的同學或者老師交流,但是不能夠共享程式碼和抄襲; 類似的庫或頻繁模式挖掘演算
頻繁項集挖掘Apriori演算法及其Python實現
Apriori演算法是通過限制候選產生髮現頻繁項集。 Apriori演算法使用一種稱為逐層搜尋的迭代方法,其中k項集用於探索(k+1)項集。首先,通過掃描資料庫,累計每個項的計數,並收集滿足最小支援度的項,找出頻繁1項集的集合,記為L1。然後,使用L1找出頻繁
海量資料探勘MMDS week4: 推薦系統之資料降維Dimensionality Reduction
海量資料探勘Mining Massive Datasets(MMDs) -Jure Leskovec courses學習筆記 推薦系統Recommendation System之降維Dimensionality Reduction{部落格內容:推薦系統有一種推薦稱作隱語義模型
【Python資料探勘課程】八.關聯規則挖掘及Apriori實現購物推薦
這篇文章主要介紹三個知識點,也是我《資料探勘與分析》課程講課的內容。 1.關聯規則挖掘概念及實現過程; 2.Apriori演算法挖掘頻繁項集; 3.Python實現關聯規則挖掘及置信度、支援度計算。一. 關聯規則挖掘概
跟我一起資料探勘(20)——網站日誌挖掘
收集web日誌的目的 Web日誌挖掘是指採用資料探勘技術,對站點使用者訪問Web伺服器過程中產生的日誌資料進行分析處理,從而發現Web使用者的訪問模式和興趣愛好等,這些資訊對站點建設潛在有用的可理解的未知資訊和知識,用於分析站點的被訪問情況,輔助站點管理和決策支援等。 1、
R語言包arules進行頻繁項集挖掘的最簡單例子
arules是進行頻繁項集挖掘(frequent itemset mining)的有效工具,不過我在使用的時候發現網上很多例子都比較繁瑣,這裡總結一下其中apriori方法的最簡單使用方法,這裡首先給出程式碼:files_change<-read.transaction
關聯規則(頻繁項集)——Apriori
1.該問題最初是對“購物籃”提出來的,著名例子是“尿布與啤酒”。 2.相關概念: 關聯規則的支援度:Support(A,B)=包含A和B的事務數/事務總數 關聯規則的置信度:Confidence(A,B)= 包含A和B的事務數/包含A事務數 頻繁項集:項集的頻率大於等
頻繁項集挖掘之apriori和fp-growth
Apriori和fp-growth是頻繁項集(frequent itemset mining)挖掘中的兩個經典演算法,主要的區別在於一個是廣度優先的方式,另一個是深度優先的方式,後一種是基於前一種效率較低的背景下提出來的,雖然都是十幾年前的,但是理解這兩個演算法對資料探勘
頻繁項集挖掘演算法——Apriori演算法
前言 關聯規則就是在給定訓練項集上頻繁出現的項集與項集之間的一種緊密的聯絡。其中“頻繁”是由人為設定的一個閾值即支援度 (support)來衡量,“緊密”也是由人為設定的一個關聯閾值即置信度(confidence)來衡量的。這兩種度量標準是頻繁項集挖掘中兩個至關
頻繁項集挖掘演算法——Eclat演算法
前面介紹過的Apriori演算法和FP-growth演算法都是從TID項集格式(即{TID:itemset})的事務集中挖掘頻繁模式,其中TID是事務識別符號,而itemset是事務TID中購買的商品。這種資料格式稱為水平資料格式。或者,資料也可以用項-TID
資料探勘之關聯分析二(頻繁項集的產生)
頻繁項集的產生 格結構(lattice structure)常常用來表示所有可能的項集。 發現頻繁項集的一個原始方法是確定格結構中每個候選項集的支援度。但是工作量比較大。另外有幾種方法可以降低產生頻繁項集的計算複雜度。 1. 減少候選項集的數目。如先驗
資料探勘中的模式發現(一)頻繁項集、頻繁閉項集、最大頻繁項集
Frequent Itemset(頻繁項集) 稱I={i1,i2,...,im}I=\{i_1, i_2, ..., i_m\}I={i1,i2,...,im}為項(Item)的集合,D={T1,T2,...,Tn}D=\{T_1, T_2, ...,T_
資料探勘之頻繁項集分析
頻繁項集最經典和常用的應用就是超市的購物籃分析。每個購物籃裡有很多商品,每個商品都是一項元素,每個購物籃都是一個集合,所有購物籃就形成了一個系列集合。 分析哪些商品經常一起頻繁出現在購物籃內,即找到頻繁項集,然後,再分析其他商品與頻繁項集的關係,即關聯規則。 1. 什麼是
資料探勘之挖掘頻繁模式的基本概念及方法
摘自《DATA MINING:Concepts and Techniques》一書,以及個人理解,主要為自己鞏固和總結,如有紕漏和出錯的地方,還請指出。此書第六章開頭指出 頻繁模式(frequent pattern),是指頻繁地出現在資料集中的模式,譬如項集,子序列或子
【資料探勘筆記六】挖掘頻繁模式、關聯和相關性:基本概念和方法
6.挖掘頻繁模式、關聯和相關性:基本概念和方法 頻繁模式(frequent pattern)是頻繁地出現在資料集中的模式。 6.1 基本概念 頻繁模式挖掘搜尋給定資料集中反覆出現的聯絡,旨在發現大型事務或關係資料集中項之間有趣的關聯或相關性,其典型例子就是購物籃分析。 購物
【資料探勘概念與技術】學習筆記6-挖掘頻繁模式、關聯和相關性:基本概念和方法(編緝中)
頻繁模式是頻繁地出現在資料集中的模式(如項集、子序列或子結構)。頻繁模式挖掘給定資料集中反覆出現的聯絡。“購物籃”例子,想象全域是商店中商品的集合,每種商品有一個布林變數,表示該商品是否出現。則每個購物籃可以用一個布林向量表示。分析布林向量,得到反映商品頻繁關聯或同時購買的購買模式。這些模式可用關聯規則來表示
【資料探勘學習筆記】10.頻繁模式挖掘基礎
一、基本概念頻繁模式– 頻繁的出現在資料集中的模式– 項集、子序或者子結構動機– 發現數據中蘊含的事物的內在規律• 項(Item) – 最小的處理單位 – 例如:Bread, Milk• 事務(Transaction) – 由事務號和項集組成 – 例如:<1, {Bre