Matlab從入門到精通(六)--矩陣基本運算
1、行向量的定義
rowvec = [1.2 3 56];
2、列向量的定義
colvec = [1.2;3;56];
3、逐個元素的分配矩陣
B(1,1) = 1 ;
B(1,2) = 2 ;
B(2,1) = 3 ;
B(2,2) = 4 ;
B =
1 2
3 4
注意:矩陣的下標從1開始計數
4、矩陣的輸入
直接輸入矩陣時候,矩陣元素用“空格”或者“逗號”隔開,矩陣行用“分號”隔離,整個矩陣放在方括號“[ ]”內.不必事先對矩陣維數做任何說明.
例如:
A = [1,2,3;4,5,6;7,8,9]
或者
A = [1 2 3;4 5 6;7 8 9]
還可以分行輸入:
A=[1 2 3;
4 5 6;
7 8 9]
注意:
表達符號一定要在英文狀態下輸入.MATLAB對矩陣大小寫是敏感的.如果不用clear指令清楚,或者重新賦值,那麼該矩陣就會一直儲存在工作空間中,直到指令窗(Command Window)關閉.
5、矩陣、零矩陣和單位矩陣
1矩陣的所有元素全為1,零矩陣的所有元素全為零.
ones(n) %建立一個n×n的1矩陣
ones(m,n,……,p) %建立一個m×n×……×p的1矩陣
ones(size(A)) %建立一個和矩陣A同樣大小的1矩陣
zeros(n) %建立一個n×n的0矩陣
zeros(m,n,……,p) %建立一個m×n×……×p的0矩陣
zeros(size(A)) %建立一個和矩陣A同樣大小的0矩陣
eye(n) %建立一個n×n的單位矩陣
eye(m,n) %建立一個m×n的單位矩陣
eye(size(A)) %建立一個和矩陣A同樣大小的單位矩陣
例如:輸入OneMatrix = ones(2,3,2)
則結果為:
OneMatrix(:,:,1) =
1 1 1
1 1 1
OneMatrix(:,:,2) =
1 1 1
1 1 1
注意:eye命令只能用來建立二維矩陣
6、隨機數和隨機矩陣
rand %產生在0~1之間均勻分佈的隨機數;每呼叫一次給一個新的數值.
rand + i*rand %產生一個複數隨機數
rand(n) %產生一個n×n的矩陣,其元素均為0~1之間均勻分佈的隨機數.
rand(m,n,……,p) %產生一個m×n×……×p的矩陣,其元素均為0~1之間均勻分佈的隨機數.
randn %產生零均值、單位方差的正太分佈隨機數
randn(n) %產生一個n×n的矩陣,其元素均為零均值、單位方差的正太分佈隨機數.
randn(m,n,……,p) %產生一個m×n×……×p的矩陣, 其元素均為零均值、單位方差的正太分佈隨機數.
7、隨機數種子
rand(‘state’) %返回一個有35個元素的向量,其中包含隨機發生器的當前狀態.
rand(‘state’,s) %設定隨機種子發生器的狀態為s
rand(‘state’,0) %設定隨機種子發生器為它的原始狀態
rand(‘state’,j) %設定隨機種子發生器為它的第j種子狀態,j為整數
rand('state',sum(100*clock)); %使用clock命令,使得隨機種子發生器在每個不同的時刻都設定為不同的狀態.
rand(‘state’,arg) %使用MATLAB中的隨機種子發生器.
randn(‘state’,) %返回一個有兩個元素的向量,其中包含正態隨機種子發生器的狀態
randn(‘state’,arg) %根據arg設定正態隨機種子發生器,見rand.
例如
astate = rand('state'); astate(1:5)
ans =
0.8651
0.5121
0.9021
0.8186
0.6267
說明:astate(1:5)表示列出狀態向量(35個元素)中的前5個元素的值
8、從已存在的向量中產生新的矩陣(一)
diag(A) %生成一個由矩陣A主對角線元素組成的列向量,主對角線總是從矩陣左上角開始,對於方陣來說它結束於矩陣的右下角.
diag(x) %x為一個n維向量.生成一個n維方陣,它的主對角線元素取自向量x,其餘元素的值都為零.
diag(A,k) %生成一個由矩陣A第k條對角線元素組成的列向量。k=0為主對角線;K<0為主對角線下第條對角線;k>0為主對角線上第K條對角線.
dialog(x,k) %生成一個(n +)*(n+)維的矩陣,該矩陣的第k條對角線元素取自x,其餘元素為0.(n為x的維數)
例一:
A =
1 2 3
4 5 6
7 8 9
diag(A)=
1
5
9
例二:
x = [1 2 3];
diag(x) =
1 0 0
0 2 0
0 0 3
例三:(A為例一中的A)
diag(A,0) =
1
5
9
diag(A,1) =
2
6
diag(A,-1) =
4
8
例四:(x為例二中的x)
diag(x,1) =
0 1 0 0
0 0 2 0
0 0 0 3
0 0 0 0
diag(x,-2) =
0 0 0 0 0
0 0 0 0 0
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
9、從已存在的矩陣中生成新的矩陣(二)
triu(A) %生成一個和A同樣大小的上三角矩陣。該矩陣的主對角線及以上元素取自A中的相應元素,其餘元素都為0.
triu(A,k) %生成一個和A同樣大小的上三角矩陣。該矩陣的第k條對角線及以上元素取自A中的相應元素,其餘元素都為0.命令triu(A,0)等價於triu(A).
tril(A) %生成一個和A同樣大小的下三角矩陣。該矩陣的主對角線及以下元素取自A中的相應元素,其餘元素都為0.
tril(A,k) %生成一個和A同樣大小的下三角矩陣。該矩陣的第k條對角線及以下元素取自A中的相應元素,其餘元素都為0.命令tril(A,0)等價於tril(A).
對於每一個方陣A都有以下關係:
A = triu(A) +tril(A) – diag(diag(A));
A = triu(A,1) + tril(A,-1) + daig(diag(A)).
例一:
A =
1 2 3
4 5 6
7 8 9
triu(A) =
1 2 3
0 5 6
0 0 9
triu(A,1) =
0 2 3
0 0 6
0 0 0
tril(A,-1) =
0 0 0
4 0 0
7 8 0
例二:
B =
1 2 3 4
5 6 7 8
9 1 0 5
triu(B) =
1 2 3 4
0 6 7 8
0 0 0 5
tril(B,-1) =
0 0 0 0
5 0 0 0
9 1 0 0
10、矩陣旋轉和矩陣變維


例一:
A =
1 2
3 4
5 6
fliplr(A) = flipdim(A,2) =
2 1
4 3
6 5
例二:
B =
2 2 3
4 6 6
7 8 10
flipud(B) = flipdim(B,1) =
7 8 10
4 6 6
2 2 3
例三:(例二中的B)
rot90(B) =
3 6 10
2 6 8
2 4 7
例四:(例二中的B)
rot90(B,2) =
10 8 7
6 6 4
3 2 2
例五:
OneMatrix = ones(3,4,2)
reshape(OneMatrix,3,8) =
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
例六:(例二中的B)
repmat(B,2,3) =
2 2 3 2 2 3 2 2 3
4 6 6 4 6 6 4 6 6
7 8 10 7 8 10 7 8 10
2 2 3 2 2 3 2 2 3
4 6 6 4 6 6 4 6 6
7 8 10 7 8 10 7 8 10
例七:
y = 3 ;
repmat(y,2,5) =
3 3 3 3 3
3 3 3 3 3
例八:
E =
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
C = zeros(3,8);
D = cat(3,E,C)
ans(:,:,1) =
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
ans(:,:,2) =
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
即在矩陣E中增加了一層零元素.
11、矩陣維數的擴充套件
(1)擴充套件列向量的列
將向量x=[9,10]擴充套件成xnew=[9,10,3,2],有下列辦法:
方法一:xnew = x ;xnew(3) = 3 ;xnew(4) = 2;
方法二:xnew = [x 3 2];
方法三:tmp = [0,15]; xnew = [x tmp];
(2)擴充套件矩陣的列
將 A = [1 2;3 4]擴充套件成Anew = [1 2 11;3 4 12],有下列方法:
方法一:y = [11;12],Anew = [A y];
方法二:Anew = [A [11;12]]
(3)擴充套件矩陣的行
將A = [1 2;3 4]擴充套件成Anew = [1 2;3 4;13 14],有下列辦法:
方法一:z = [13 14],Anew = [A; z]
方法二:Anew = [A;[13 14]]
(4)矩陣的賦值擴充套件法
A = reshape(1:9,3,3)
A =
1 4 7
2 5 8
3 6 9
A(4,4) = 111;
A =
1 4 7 0
2 5 8 0
3 6 9 0
0 0 0 111
A(:,6) = 222
A =
1 4 7 0 0 222
2 5 8 0 0 222
3 6 9 0 0 222
0 0 0 111 0 222
A(5,:) = 250
A =
1 4 7 0 0 222
2 5 8 0 0 222
3 6 9 0 0 222
0 0 0 111 0 222
250 250 250 250 250 250
12、數字序列
(1)數字序列一
i:k %建立從i開始、步長為1、到k結束的數字序列.數字i和k不一定是整數,該序列最後一個數小於或等於k.
i:j:k %建立建立從i開始、步長為j、到k結束的數字序列.數字i、j和k不一定是整數,該序列最後一個數小於或等於k.
(2)數字序列二
linspace(a,b) %在區間[a,b]上建立一個有100個元素的向量,這100個數把整個區間線性分隔.
linspace(a,b,n) %在在區間[a,b]上建立一個有n個元素的向量,這n個數把整個區間線性分隔.
logspace(a,b) %在區間[10*a,10*b]上建立一個有50個元素的向量,這50個數把整個區間對數分隔.
logspace(ab,n) %在區間[10*a,10*b]上建立一個有n個元素的向量,這n個數把整個區間對數分隔.
例一:
vect = 2:7
vect = 2 3 4 5 6 7
vect = 2:7.2
vect = 2 3 4 5 6 7
vect = 6:-1:2
vect = 6 5 4 3 2
vect = 1.2:-0.8:-3.2
1.2000 0.4000 -0.4000 -1.2000 -2.0000 -2.8000
注意:此時最後一個數為-2.8.
例二:
linspace(1,5,6)
ans =
1.0000 1.8000 2.6000 3.4000 4.2000 5.0000
13、定義子陣
A(i,j,……,k) %返回多維陣列A中下標為(i,j,……,k)的元素值.
A(:,j) %返回二維矩陣A中第j列列向量.
A(i,:) %返回二維矩陣A中第j行行向量.
A(:,j:k) %返回二維矩陣A中的第j列,第j+1列,……,第k列列向量組成的子陣.
A(i:k,:) %返回二維矩陣A中的第i行,第i+1行,……,第k行行向量組成的子陣.
A(i:k,j:L) %返回二維矩陣A中的第i行到第k行行向量和第j列到第L列列向量組成的子陣.
A(:,:,……,:) %返回矩陣A本身.
A(:) %將矩陣A中的每列合成一個長的列向量.
A(j:k) %返回一個行向量,其中的元素為A(:)中的從第j個元素到第k個元素.
A([j1,j2,……]) %返回一個行向量,其中的元素為A(:)中的第j1,j2,……元素.
A(:,[j1,j2,……]) %返回矩陣A的第j1列、第j2列、……的列向量.
A([j1,j2,……],:) %回矩陣A的第j1行、第j2行、……的行向量.
A([i1,i2,……],[j1,j2,……]) %返回矩陣第i1行、第i2行等和第j1列、第j2列等的元素.
14、將二維矩陣合成三維矩陣
>> A1 = [1 2;3 4];
>> A2 = [3 4 ;5 6];
>> C(:,:,1)=A1;
>> C(:,:,2)=A2;
>> C
C(:,:,1) =
1 2
3 4
C(:,:,2) =
3 4
5 6
此時C為三維矩陣.
15、刪除矩陣的行
【例一】
>> a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> a = a([2,3],:)
a =
4 5 6
7 8 9
【例二】
>> a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> a(1,:) = []
a =
4 5 6
7 8 9
16、刪除矩陣的列
【例一】
>> a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> a = a(:,[1,3])
a =
1 3
4 6
7 9
【例二】
>> a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> a(:,2) = []
a =
1 3
4 6
7 9
17、陣列定址和排序

18、矩陣及陣列運算
18.1矩陣加減
兩矩陣必須同階才可進行加減運算,另外MATLAB還特別作了擴充,允許矩陣與一個數量(即1×1矩陣)進行加減運算。
例如鍵入A=[1,2,3;4,5,6;7,8,9],B=[1,4,7;2,5,8;3,6,9],則 C=A+B 的結果顯示為:
如果鍵入x=[-1,0,2],則y=x-1的結果為:
18.2矩陣乘法
當左乘矩陣的列數等於右乘矩陣的行數時,兩矩陣可以進行乘法。在MATLAB中,矩陣A乘以矩陣B應表示成A*B。
18.3矩陣除法
MATLAB中有兩種除法,即左除“\”與右除“/”。
若A為非奇異方陣,B為矩陣,則A\B,B/A的數學意義分別為 。在MATLAB中,這兩種運算也可以分別表示為inv(A)*B,B*inv(A)。
18.4陣列的乘除運算

18.5陣列的乘方
陣列的乘方用符號“.^”來表示,而陣列的乘方有三種形式。
1 向量的向量次方
例如:鍵入x =[1,2,3], y =[4,5,6],z=x.^y,則結果為:
z=
1 32 729
它的數學意義是 。
2 向量的數量次方
例如:鍵入x =[1,2,3],z=x.^2,則結果為:
z=
1 4 9
它的數學意義是 。
3 數量的向量次方
例如:鍵入x =[1,2,3],z=2.^x,則結果為:
z=
2 4 8
它的數學意義是 。
19、向量的關係運算
MATLAB提供了6種關係運算符:<(小於)、<=(小於或等於)、>(大於)、 >=(大於或等於)、 ==(等於)、 ~=(不等於)。
關係運算的運演算法則為:
1 當兩個比較量是標量時,直接比較兩數的大小。若關係成立,關係表示式的值為1,否則為0。
2 當參與比較的量是兩個維數相同的矩陣時,比較是對兩矩陣相同位置的元素按標量關係運算規則逐個進行,並給出元素比較結果。最終的關係運算的結果是一個維數與原矩陣相同,它的元素由0或1組成。
3 當參與比較的一個是標量,而另一個是矩陣時,則把標量與矩陣的每一個元素按標量關係運算規則逐個比較,並給出元素比較結果。最終的關係運算結果是一個維數與原矩陣相同的矩陣,它的元素由0或1組成。
例如
若鍵入x=(1<2)
則x =
1
若鍵入A=[1,2,3;2,3,4],B=[1,2,2;2,2,3],C=(A<=B)
則 C =
1 1 0
1 0 0
若鍵入A=[1,2,3;2,3,4],b=1,C=(A<=b)
則 C =
1 0 0
0 0 0
20、向量的邏輯運算
MATLAB提供了3種邏輯運算子:&(與)、|(或)、~(非)。
邏輯運算的運演算法則為:
1 在邏輯運算中,確認非零元為真,用1表示,零元素為假,用0表示。
2 設參與邏輯運算的是兩個標量a和b,那麼
a&b a,b全為非零時,運算結果為1,否則為0。
a|b a,b中只要有一個非零時,運算結果為1;只有當a,b全為零時,運算結果為0。
~a 當a為零時,運算結果為1;當a非零時,運算結果為0。
3 若參與邏輯運算的是兩個同維矩陣,那麼運算將對矩陣相同位置上的元素按標量規則逐個進行。最終運算的結果是一個與原矩陣同維的矩陣,其元素由0或1組成。
4 若參與邏輯運算的一個是標量,一個是矩陣,那麼運算將在標量與矩陣中的每個元素之間按標量規則逐個進行。最終運算結果是一個與矩陣同維的矩陣,其元素是由0或1組成。
5 若對一個矩陣做邏輯非運算,那麼將對矩陣中的每個元素按標量規則逐個取邏輯非,最終運算的結果是一個與原矩陣同維的矩陣,其元素由0或1組成。
6 在算術、關係、邏輯運算中,算術運算優先順序最高,邏輯運算優先順序最低。
例如,若鍵入A=[0,2,3;0,2,0],B=[0,0,0;2,3,4],A&B,A|B,~A,則其結果分別為
ans =
0 0 0
0 1 0
ans =
0 1 1
1 1 1
ans =
1 0 0
1 0 1
21、判斷矩陣是否為空
Isempty(Matrix) ;
如果矩陣為空則返回1,否則返回0;
22、求行列式及化階梯形
【例一】:求矩陣A的行列式:det(A)
例:A=[1 2;3 4] ;
則det(A) = -2 ;
【例二】:化階梯形
A =
4 5 6
1 2 3
7 8 9
>> rref(A)
ans =
1 0 -1
0 1 2
0 0 0
23、求矩陣的轉置及矩陣的秩
23.1矩陣的轉置
求矩陣A的轉置矩陣:A’
轉置符號為單引號.
23.2求矩陣的秩
例:
>> X = [1 3 5;5 -9 0; 32 1 18];
>> rank(X)
ans =
3
24、求矩陣的逆矩陣及跡
求矩陣A的逆矩陣:inv(A)
求矩陣A的跡:trace(A)
例:a= [1 2;3 4];
則
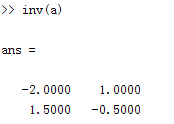
trace(A) = 5.
25、矩陣及向量的最大值、最小值
25.1向量的最大值及最小值
- max(P) :返回向量P的最大值,如果P中包含複數元素,則按模取最大值。
- [y,i] = max(P) :返回向量P的最大值存入y,最大值的序號存入i,如果P中包含複數元素,則按模取最大值。
- 求向量的最小值的函式min(P)用法同max(P)。
25.2矩陣的最大值及最小值
- max(A) : 返回一個行向量,向量的第i個元素為矩陣A的第i列的最大值。
- [y,u] = max(A) : 返回行向量y和u,y記錄A的每列的最大值,u記錄每列最大值的行號。
- max(A,[],dim) : dim取1時,該函式和max(A完全相同;dim取2時,該函式返回一個列向量,其第i個元素是A矩陣的第i行的最大值。
- 求矩陣的最小值函式min(A)用法同max(A)。
- 使用max(max(A))可以求出矩陣中的最大元素,同理min(min(A))可以求出矩陣中的最小元素。
26、計算矩陣大小及元素個數
26.1計算矩陣大小
size(A),返回的是矩陣A的列數和行數;
size(A,1),返回矩陣A的行數;
size(A,2),返回矩陣A的列數。
>>A = [1 2 5;3 4 9];
則size(A) = 2 3
size(A,1) = 2
size(A,2) = 3
26.2計算矩陣中的元素個數
使用函式numel()
當矩陣為一個行向量或者一個列向量時候,返回的該向量的長度,當矩陣為M*N時,返回值為M*N.
例:A = [1 2 3 4;5 6 7 8];
則numel(A) = 8.
26.3計算矩陣的維數
n = ndims(A);返回矩陣的維數,若A為三維陣列,則n=3.
27、LU分解
矩陣的三角分解又稱LU分解,它的目的是將一個矩陣分解成一個下三角矩陣L和一個上三角矩陣U的乘積,即A=LU。
函式: lu
格式 [L,U] = lu(X) %U為上三角陣,L為下三角陣或其變換形式,滿足LU=X。
[L,U,P] = lu(X) %U為上三角陣,L為下三角陣,P為單位矩陣的行變換矩陣,滿足LU=PX。
例:
>> X = [1 3 5;5 -9 0; 32 1 18];
>> [p,q,r] = lu(X)
p =
1.0000 0 0
0.1563 1.0000 0
0.0313 -0.3242 1.0000
q =
32.0000 1.0000 18.0000
0 -9.1563 -2.8125
0 0 3.5256
r =
0 0 1
0 1 0
1 0 0
28、QR分解(求正交矩陣)
將矩陣A分解成一個正交矩陣與一個上三角矩陣的乘積。
函式: qr
格式: [Q,R] = qr(A) %求得正交矩陣Q和上三角陣R,Q和R滿足A=QR。
例:
>> X = [1 3 5;5 -9 0; 32 1 18];
>> [p ,q] = qr(X)
p =
0.0309 0.3156 0.9484
0.1543 -0.9390 0.3075
0.9875 0.1368 -0.0777
q =
32.4037 -0.3086 17.9300
0 9.5344 4.0415
0 0 3.3436
29、求特徵值及特徵向量
函式 eig
格式 d = eig(A) %求矩陣A的特徵值d,以向量形式存放d。
【例一】
>> X = [1 3 5;5 -9 0; 32 1 18];
>> D = eig(X)
D =
24.8632
-3.7328
-11.1305
【例二】
>> X = [1 3 5;5 -9 0; 32 1 18];
>> [d,v] = eig(X)
d =
-0.2087 -0.4880 0.3641
-0.0308 -0.4632 -0.8545
-0.9775 0.7398 -0.3706
v =
24.8632 0 0
0 -3.7328 0
0 0 -11.1305
說明:矩陣d的列向量構成特徵向量,v中的正對角線上的元素為特徵值。
30、奇異值分解
函式 svd
格式 s = svd (X) %返回矩陣X的奇異值向量
[U,S,V] = svd (X) %返回一個與X同大小的對角矩陣S,兩個酉矩陣U和V,且滿足= U*S*V'。若A為m×n陣,則U為m×m陣,V為n×n陣。奇異值在S的對角線上,非負且按降序排列。
[U,S,V] = svd (X,0) %得到一個“有效大小”的分解,只計算出矩陣U的前n列,矩陣S的大小為n×n。
【例】:
>> X = [1 3 5;5 -9 0; 32 1 18];
>> S = svd(X)
S =
37.1225
10.2231
2.7220
>> [U,S,V] = svd(X)
U =
-0.0902 0.4116 -0.9069
-0.1159 -0.9088 -0.4009
-0.9892 0.0689 0.1296
S =
37.1225 0 0
0 10.2231 0
0 0 2.7220
V =
-0.8707 -0.1885 0.4543
-0.0058 0.9276 0.3736
-0.4918 0.3227 -0.8087
>> [U,S,V] = svd(X,0)
U =
-0.0902 0.4116 -0.9069
-0.1159 -0.9088 -0.4009
-0.9892 0.0689 0.1296
S =
37.1225 0 0
0 10.2231 0
0 0 2.7220
V =
-0.8707 -0.1885 0.4543
-0.0058 0.9276 0.3736
-0.4918 0.3227 -0.8087
