馬爾科夫決策過程MDP - Lecture Note for CS188(暨CS181 ShanghaiTech)

阿新 • • 發佈：2018-11-25

說明：筆記旨在整理我校CS181課程的基本概念(PPT借用了Berkeley CS188)。由於授課及考試語言為英文，故英文出沒可能。

1 Markov Decision Processes mechanics

1.1 Markov Decision definitions

1.2 Markov 涵義

1.3 最優策略optimal policy

1.4 MDP搜尋樹 MDP search tree

2 Solving MDPs

2.1 Optimal Quantities

1 Markov Decision Processes mechanics

1.1 Markov Decision definitions

A MDP is defined by:

1.2 Markov 涵義

For markov decision processes, "Markov" means action outcomes depend only on the current state:

$P(S_{t+1}=s'|S_t=s_t, A_t=a_t, S_{t-1}=s_{t-1}, A_{t-1},\cdots S_0=s_0) = P(S_{t+1}=s'|S_t=s_t, A_t=a_t)$

1.3 最優策略optimal policy

For MDP, we want an optimal policy $\pi^*: S \mapsto A$ :

A policy π gives an action for each state
An optimal policy is one that maximizes expected utility if allowed
An explicity policy defines a reflex agent

1.4 MDP搜尋樹 MDP search tree

5. Discounting: each time we descend a level, we multiply in the discount once. Redefine Rewards R(s, a, s') with discount γ

2 Solving MDPs

2.1 Optimal Quantities

1. The value (utility) of a state s: $V^*(s)$ =expected utility starting in s and acting optimally.

2. The value (utility) of a q-state (s,a): $Q^*(s,a)$ =expected utility starting out having taken action a from state s and (therefore) acting optimally

3. The optimal policy: $\pi^*(s)$ =optimal action from state s

2.2 Value of states

2.3 Value iteration

1.Define $V_k(s)$ to be the optimal value of s if the game ends in k more time steps

2.Policy extraction

$\pi^*(s)=\arg \max_a \sum_{s'} T(s, a, s')[R(s, a, s')+\gamma V^*(s')]=\arg \max_a Q^*(s, a)$

2.4 Policy iteration

Step1 Policy evaluation:

Step2: Policy improvement: After evaluation(step 1), we get $v^{\pi_i}(s')$

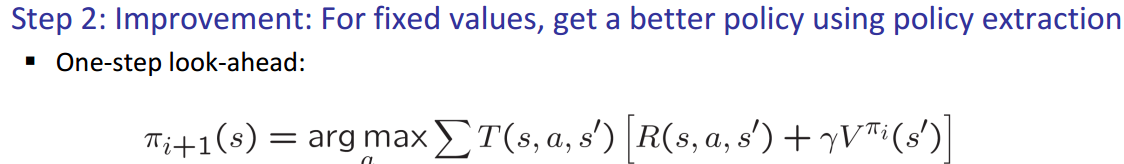
Policy iteration: repeat two steps until policy converges

Reference

1. Artificial Intelligence, A Modern Approach. 3rd Edition. Stuart R., Peter N. Chapter 17

2. UC berkeley, CS188. Lecture 13 Markov Decision Process

馬爾科夫決策過程MDP - Lecture Note for CS188(暨CS181 ShanghaiTech)

說明：筆記旨在整理我校CS181課程的基本概念(PPT借用了Berkeley CS188)。由於授課及考試語言為英文，故英文出沒可能。目錄 1 Markov Decision Processes mechanics 1.1 Markov Decision

強化學習(David Silver)2：MDP(馬爾科夫決策過程)

war 觀察 turn 解法求解有關馬爾科夫函數使用 1、MP(馬爾科夫過程) 1.1、MDP介紹 1）MDP形式化地強化學習中的環境(此時假設環境完全可以觀察) 2) 幾乎所有強化學習問題都可以形式化為MDP(部分可觀察的環境也可以轉化為MDP????) 1.2

強化學習（RLAI）讀書筆記第三章有限馬爾科夫決策過程（finite MDP）

第三章有限馬爾科夫決策過程有限馬爾科夫決策過程（MDP）是關於評估型反饋的，就像多臂老虎機問題裡一樣，但是有是關聯型的問題。MDP是一個經典的關於連續序列決策的模型，其中動作不僅影響當前的反饋，也會影響接下來的狀態以及以後的反饋。因此MDP需要考慮延遲反饋和當前反饋與延遲反饋之間的交換。

深度強化學習2——馬爾科夫決策過程（MDP）

本文講解思路從馬科夫過程（MP) 到馬爾科夫獎勵過程（MRP）最後到馬爾科夫決策過程（MDP）。首先我們要了解馬爾科夫性，在上一章1.3我們也提到，當前狀態包含了對未來預測所需要的有用資訊，過去資訊對未來預測不重要，該就滿足了馬爾科夫性，嚴格來說，就是某一狀態資訊包含了所

增強學習（一）——馬爾科夫決策過程（MDP）

最近因為研究需要，要開始學習機器學習了。之前只是懂些CNN什麼的皮毛，對機器學習的整體認識都比較缺乏，後面我會從頭開始一點點打基礎，正好也用部落格把自己的學習歷程記錄一下，如果有大牛看到博文中

馬爾科夫決策過程

技術分享 mar silver 接下來馬爾科夫 ima gamma nbsp 給定馬爾科夫特性：下一時刻的狀態只與現在的時刻的狀態相關，與之前的時刻無關，即狀態信息包含了歷史的所有相關信息。馬爾科夫獎勵過程，$<S, P, R, \gamma>$：

從馬爾科夫決策過程到強化學習（From Markov Decision Process to Reinforcement Learning）

從馬爾科夫決策過程到強化學習（From Markov Decision Process to Reinforcement Learning）作者：Bluemapleman([email protected]) Github：https://github.com/blu

Udacity強化學習系列（二）—— 馬爾科夫決策過程（Markov Decision Processes）

說到馬爾科夫Markov，大家可能都不陌生，陌生的[連結往裡走](https://baike.baidu.com/item/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E8

David Silver強化學習公開課（一）：馬爾科夫決策過程

在強化學習中，馬爾科夫決策過程（Markov decision process, MDP）是對完全可觀測的環境進行描述的，也就是說觀測到的狀態內容完整地決定了決策的需要的特徵。幾乎所有的強化學習問題都可以轉化為MDP。本講是理解強化學習問題的理論基礎。馬爾科夫過程 M

簡述馬爾科夫決策過程（下）

都是自己人工智能直接 enter 知識一次自己的初步在上一篇文章中我們給大家介紹了很多關於馬爾科夫決策知識，具體來說就是馬爾科夫決策過程的特點、要求以及定義，這些內容都是能夠幫助大家初步了解馬爾科夫決策過程的。我們在這篇文章中詳細為大家介紹關於馬爾科夫決策過

強化學習簡介及馬爾科夫決策過程

1. 什麼是強化學習強化學習（reinforcement learning, RL）是近年來大家提的非常多的一個概念，那麼，什麼叫強化學習？強化學習是機器學習的一個分支，和監督學習，非監督學習並列。參考文獻[1]中給出了定義： Reinforcement learning is learn

強化學習-MDP(馬爾可夫決策過程)算法原理

取值執行環境 person 今天還需 huang 復雜屬性 1. 前言前面的強化學習基礎知識介紹了強化學習中的一些基本元素和整體概念。今天講解強化學習裏面最最基礎的MDP（馬爾可夫決策過程）。 2. MDP定義 MDP是當前強化學習理論推導的基石，通過這套框架，強

強化學習入門基礎——馬爾可夫決策過程（MDP）

## MDP背景介紹 ### Random Variable **隨機變數（Random Variable）**，通常用大寫字母來表示一個隨機事件。比如看下面的例子： $X$: 河水是鹹的 $Y$: 井水是甜的很顯然，$Y$, $Y$兩個隨機事件是沒有關係的。也就是說$X$和$Y$之間**是相互獨

強化學習入門基礎-馬爾可夫決策過程（MDP）

> 作者：YJLAugus 部落格： https://www.cnblogs.com/yjlaugus 專案地址：https://github.com/YJLAugus/Reinforcement-Learning-Notes，如果感覺對您有所幫助，煩請點個⭐Star。 ## MDP背景介紹 ### R

馬爾可夫決策過程中的動規

next 獲得步驟 bre 處理技術分享證明 mat 狀態空間 RL學習路線記錄強化學習入門的相關算法及實現。 DP Policy Evaluation 通過以下步驟進行同步backup，從而評估一個給定的 policy ：在第 $k+1$ 輪，對於所有狀態

【RL系列】馬爾可夫決策過程——狀態價值評價與動作價值評價的統一

ice .html .net bsp cor python-r and text 系列請先閱讀上兩篇文章：【RL系列】馬爾可夫決策過程中狀態價值函數的一般形式【RL系列】馬爾可夫決策過程與動態編程狀態價值函數，顧名思義，就是用於狀態價值評價（SVE）的。典型的問

[第16集] 馬爾可夫決策過程/增強學習

src 映射 height com http image 分享 nbsp 分享圖片，前面的符號是數學上的映射 [第16集] 馬爾可夫決策過程/增強學習

強化學習（二）：馬爾可夫決策過程

最優最大值公式 des 版本 ams 強化學習有獎 RoCE Finite Markov Decision Process 馬爾可夫決策過程(MDP)是對連續決策進行建模，當前的動作不僅對當前產生影響，而且還會對將來的的情況產生影響，如果從獎勵的角度，即MDP不僅影響

馬爾可夫決策過程

直接 mic async 兩種 bellman states force sum 它的馬爾可夫決策過程概述現在我們開始討論增強學習(RL，reinforcement learning)和自適應控制( adaptive control)。在監督式學習中，我們的算法總

馬爾科夫獎賞過程

0 前言本文寫作目的：儘量通俗講解強化學習知識，使讀者不會被各種概念嚇倒！本文是第一篇，但是最關鍵的一篇是第二篇馬爾科夫決策過程(Markov Decision Process，MDP)，只有充分理解了馬爾科夫決策過程，才能遊刃有餘的學習後續知識，所以希望讀者能夠將MDP深入理解後再去學習後續

馬爾科夫決策過程MDP - Lecture Note for CS188(暨CS181 ShanghaiTech)

1 Markov Decision Processes mechanics

1.1 Markov Decision definitions

1.2 Markov 涵義

1.3 最優策略optimal policy

1.4 MDP搜尋樹 MDP search tree

2 Solving MDPs

2.1 Optimal Quantities

2.2 Value of states

2.3 Value iteration

2.4 Policy iteration

Reference

相關推薦