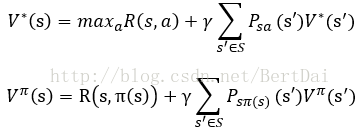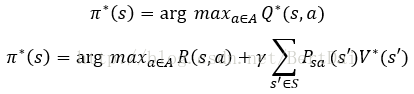最近因為研究需要，要開始學習機器學習了。之前只是懂些CNN什麼的皮毛，對機器學習的整體認識都比較缺乏，後面我會從頭開始一點點打基礎，正好也用部落格把自己的學習歷程記錄一下，如果有大牛看到博文中有錯誤，歡迎指正！

       增強學習（reinforcement learning,RL）是近年來機器學習和智慧控制領域的主要方法之一。在增強學習中有三個概念：狀態、動作和回報。

      “狀態（state）”是描述當前情況的。對一個正在學習行走的機器人來說，狀態是它的兩條腿的位置。對一個圍棋程式來說，狀態是棋盤上所有棋子的位置。

      “動作（action）”是一個智慧體在每個狀態中可以做的事情。給定一個機器人兩條腿的狀態或位置，它可以在一定距離內走幾步。通常一個智慧體只能採取有限或者固定範圍內的動作。例如一個機器人的步幅只能是0.01米到1米，而圍棋程式只能將它的棋子放在19×19路棋盤（361個位置）的某一位置。

      “回報（reward）”是一個描述來自外界的反饋的抽象概念。回報可以是正面的或者負面的。當回報是正面的時候，它對應於我們常規意義上的獎勵。當回報是負面的時候，它就對應於我們通常所說的懲罰。

       因此，增強學習的核心目標就是解決這樣的問題：一個能夠感知環境的自治agent，怎樣學習到最優動作策略π：S->A，它能在給定當前狀態S集合中的s時，從集合A中輸出一個合適的動作a。

       在研究用於尋找策略的演算法之前，我們必須充分了解馬爾科夫決策過程（MDP）。

馬爾科夫決策過程（MDP）

       在面對許多問題時，馬爾科夫決策過程為我們提供了一種對規劃和行動進行推理的形式。大家應該都知道馬爾科夫鏈(Markov Chain)，它與MDP有一個共同性質就是無後效性，也就是指系統的下個狀態只與當前狀態有關，而與更早之前的狀態無關，這一特性為我們增強學習打下了理論基礎。不同的是MDP考慮了動作，即系統下個狀態不僅和當前的狀態有關，也和當前採取的動作有關。

       因此MDP可以表示為一個元組（S, A, P_sa, R）：

• S：所有可能狀態的集合。
• A：針對每個狀態，我們都要做出動作，這些動作的集合就是A。
• P_sa：狀態轉換分佈（statetransition distribution），如果我們在狀態s中採取了動作a，系統會轉移到一個新的狀態，狀態轉換分佈描述了轉移到哪個狀態的概率分佈。
• R：回饋函式（rewardfunction），增強學習的核心概念，描述了動作能夠產生的回報。比如R_π(s,a)描述了在狀態s下采用策略π所對應的動作a的回報，也叫做立即回報，回饋函式可以有不同的表達形式。

       但是在選取最優策略的過程中，我們只看立即回報並不能判定哪種策略更優，我們希望的是在採取了策略π以後，可以使得整個狀態序列的折扣回饋最大：

R(s₀, a₀)+ γR(s₁, a₁) + γ²R(s₂, a₂)+            (1)

其中γ被稱為折扣因子，在經濟學上的解釋叫做無風險折現率（risk-freeinterest rate），意思是馬上得到的錢（回饋）比未來得到錢更有價值。

V^π(s) =E_π[ R(s₀, a₀) + γR(s₁, a₁)+ γ²R(s₂, a₂) + … | s₀= s ]

這個函式也被稱為狀態價值函式(statevalue function)，因為初始狀態s和策略π是我們給定的，動作a = π(s)。與之相對應的是動作價值函式(actionvalue function)，也叫做Q函式：

Q^π(s, a)= E_π[ R₀ + γR₁ + γ²R₂ + …| s₀= s, a₀= a]

其中的初始狀態和初始動作都是我們給定的。

函式最優與求解：

       進一步，我們定義了最優價值函式（optimalvalue function）和最優Q函式（optimal Q-function）：

V^*(s) =max_π V^π(s)

Q^*(s, a)= max_π Q^π(s, a)

       不難證明，V^*和V^π滿足下面兩個方程：

上式稱為最優貝爾曼方程，給出了V*和V^π的遞迴定義形式，也是V的求解方法。V*的公式說明了通過每一步選取最優的動作a，並在後面的動作中也保持最優，就可以得到V*。V^π的含義是：如果我們持續根據策略π來選擇動作，那麼策略π的期望回報就是當前的回報加上未來的期望回報。      

       相似的，下列對於Q函式的方程也成立：

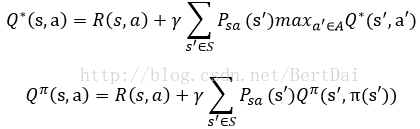
這種遞迴的定義形式也有利於我們在具體實現時的求解。

也就是說，如果我們知道了Q*，可以更加方便的計算出最優策略，而要從V*得到最優策略，還必須知道狀態轉換分佈P_sa才行。

       對於尋找最優策略的具體演算法，包括了價值迭代、策略迭代、蒙特卡洛演算法和Q學習演算法等，後期我會繼續整理。