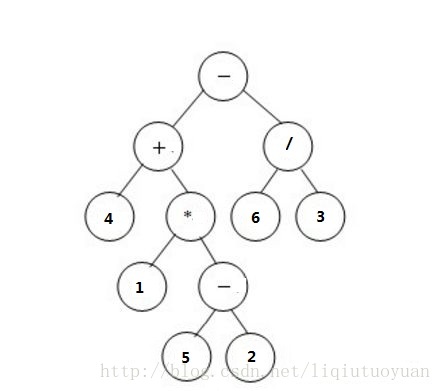
表示式樹與前中字尾表示式
電腦科學中,除了棧以外,二叉樹也是處理表達式的常用工具,為了處理表達式而遵循相應規則構造的樹被稱為表示式樹。
表示式樹
算數表示式是分層的遞迴結構,一個運算子作用於相應的運算物件,其運算物件又可以是任意複雜的表示式。樹的遞迴結構正好用來表示這種表示式。下面只討論二元表示式。
二元表示式可以很自然的聯絡到二叉樹:以基本運算物件作為葉節點中的資料;以運算子作為非葉節點中的資料,其兩棵子樹是它的運算物件,子樹可以是基本運算物件,也可以是複雜表示式。如圖是一個表示式樹。
字首、中綴和字尾表示式
中綴表示式(中綴記法)
我們平時縮寫的表示式,將運算子寫在兩個運算元中間的表示式,稱作中綴表示式。在中綴表示式中,運算子有不同的優先順序,圓括號用於改變運算順序,這使得運算規則比較複雜,求值過程不能直接從左到右順序進行,不利於計算機處理。
字尾表示式
將運算子寫在兩個運算元之後的表示式稱作字尾表示式。字尾表示式中沒有括號,並且運算子沒有優先順序。字尾表示式的求值過程能夠嚴格按照從左到右的順序進行,有利於計算機處理。
字首表示式
字首表示式是將運算子寫在兩個運算元之前的表示式。和字尾表示式一樣,字首表示式沒有括號,運算子沒有優先順序,能嚴格按照從右到左的順序計算。
另外,算式表示式和表示式樹的關係如下:
- 表示式樹的先根遍歷:字首表示式
- 表示式樹的中根遍歷:中綴表示式
- 表示式樹的後根遍歷:字尾表示式
表示式的轉換
利用表示式樹
給定一個表示式的中綴形式:(4+1*(5-2))-6/3
首先將每個運算加上括號,區分優先順序,得到(4+(1*(5-2)))-(6/3)
括號外的-優先順序最低,作為根節點,(4+(1*(5-2)))作為左子樹,(6/3)作為右子樹;
遞迴的轉換4+(1*(5-2)),+最為根節點,4是左子樹,(1*(5-2))是右子樹。*是右子樹的根節點,1是左子樹,(5-2)是右子樹。最後計算(5-2),-是根節點,5是左子樹,2是右子樹。得到的表示式樹如文章之初給出的圖。
構造好表示式樹之後,字首表示式和中綴表示式可根據先根遍歷和後根遍歷得到。
字首表示式:- + 4 * 1 - 5 2 / 6 3
字尾表示式:4 1 5 2 - * + 6 3 / -
利用棧
將中綴表示式轉換為字尾表示式
step1:初始化一個棧和一個字尾表示式字串
step2:從左到右依次對中綴表示式中的每個字元進行以下處理,直到表示式結束
- 如果字元是‘(’,將其入棧
- 如果字元是數字,新增到字尾表示式的字串中
- 如果字元是運算子,先將棧頂優先順序不低於該運算子的運算子出棧,新增到字尾表示式中,再將該運算子入棧。注意,當‘(’在棧中時,優先順序最低
- 如果字元是‘)’,將棧頂元素出棧,新增到字尾表示式中,直到出棧的是‘(’
step3:如果表示式結束,但棧中還有元素,將所有元素出棧,新增到字尾表示式中
例如給定一個表示式的中綴形式:(4+1*(5-2))-6/3,棧中元素和表示式的變化如下表所示:
| 掃描到的元素 | 棧 | 字尾表示式 | 說明 |
|---|---|---|---|
| ( | ( | 將(入棧,表示式空 | |
| 4 | ( | 4 | 將4加入表示式 |
| + | ( + | 4 | 將+入棧 |
| 1 | ( + | 4 1 | 將1加入表示式 |
| * | ( + * | 4 1 | 將*入棧 |
| ( | ( + * ( | 4 1 | 將(入棧 |
| 5 | ( + * ( | 4 1 5 | 將5加入表示式 |
| - | ( + * ( - | 4 1 5 | 將-入棧 |
| 2 | ( + * ( - | 4 1 5 2 | 將2 加入表示式 |
| ) | ( + * | 4 1 5 2 - | -出棧,加入表示式 |
| ) | 4 1 5 2 - * + | *和+出棧,加入表示式,棧空 | |
| - | - | 4 1 5 2 - * + | -入棧 |
| 6 | - | 4 1 5 2 - * + 6 | 6加入表示式 |
| / | -/ | 4 1 5 2 - * + 6 | /入棧 |
| 3 | -/ | 4 1 5 2 - * + 6 3 | 3加入表示式 |
| 4 1 5 2 - * + 6 3 / - | 表示式掃描結束,將棧中元素加入表示式 |
最後得到字尾表示式為4 1 5 2 - * + 6 3 / -
將中綴表示式轉換為字首表示式
中綴表示式轉換到字首表達的方法和轉換到字尾表示式過程一致,細節上有所變化
step1:初始化兩個棧s1 和s2
step2:從右到左依次對中綴表示式中的每個字元進行以下處理,直到表示式結束
- 如果字元是‘)’,將其入棧
- 如果字元是數字,新增到s2中
- 如果字元是運算子,先將棧頂優先順序不低於該運算子的運算子出棧,新增到s2中,再將該運算子入棧。當‘)’在棧中是,優先順序最低
- 如果字元是‘(’,將棧頂元素出棧,新增到s2中,直到出棧的是‘)’
step3:如果表示式結束,但棧中還有元素,將所有元素出棧,新增s2中
step4:將棧s2中元素依次出棧,即得到字首表示式
給定一個表示式的中綴形式:(4+1*(5-2))-6/3,其字首形式為 - + 4 * 1 - 5 2 / 6 3
表示式的計算
中綴表示式的計算我們已經非常清楚,字首和字尾表示式更適合計算機處理
字尾表示式的計算
字尾表示式沒有括號,運算子的順序即為實際運算順序,在求值過程中,當遇到運算子時,只要取得前兩個運算元就可以立即進行計算。當操作數出現時,不能立即求值,需要先儲存等待運算子。對於等待中的運算元而言,後出現的先運算,所以需要一個棧輔助操作。
字尾表示式的運算過程如下:
step1:設定一個棧
step2:從左到右對字尾表示式中的字元進行以下處理:
- 如果字元是數字,現將其轉化為數字,然後入棧
- 如果字元是運算子,出棧兩個值進行計算。計算結果入棧
- 重複以上步驟,直到字尾表示式掃描結束,棧中最後一個元素就是表示式的結果。
給定字尾表示式4 1 5 2 - * + 6 3 / -,依次將4 1 5 2 入棧,當掃描到-時,2,5出棧,計算5-2=3;將3入棧,此時棧中元素為4 1 3。接著掃描到*,3 1出棧,計算1*3=3,3入棧,棧中元素為4 3,。掃描+,3 4出棧,計算4+3=7,7入棧。接著6 3 入棧,棧中該元素為7 6 3,掃描到/,3 6出棧,計算6/3=2,2入棧,棧中元素為7 2.掃描-,2 7 出棧,計算7-2=5,5入棧。表示式掃描完畢,棧中元素為5,表示式結果為5.
字首表示式的計算
字首表示式的計算掃描順序從右到左,其他和字尾表示式的計算完全一致。
以上內容轉載自二叉樹的簡單應用–表示式樹,略加修改,給此文博主一個大大的贊,良心好文!!!本文以下內容為我對於這篇博文的一個補充。
表示式樹程式碼實現
如何給一個表示式建立表示式樹呢?方法有很多,這裡只介紹一種:找到"最後計算"的運算子(它是整棵表示式樹的根),然後遞迴處理(這也是前文介紹的方法)。下面是程式:
const int maxn = 1000;
int lch[maxn], rch[maxn]; char op[maxn];
int nc = 0; //結點數
int build_tree(char* s, int x, int y)
{
int i, cl = -1, c2 = -1, p = 0;
int u;
if(y-x == 1) //僅一個字元,建立單獨結點
{
u = ++nc;
lch[u] = rch[u] = 0; op[u] = s[x];
return u;
}
for(i = x; i < y; i++)
{
switch(s[i])
{
case '(': p++; break;
case ')': p--; break;
case '+': case '-': if(!p) c1 = i; break;
case '*': case '/': if(!p) c2 = i; break;
}
}
if(c1 < 0) c1 = c2; //找不到括號外的加減號,就用乘除號
if(c1 < 0) return build_tree(s, x+1, y-1); //整個表示式被一對括號括起來
u = ++nc;
lch[u] = build_tree(s, x, c1);
rch[u] = build_tree(s, c1+1, y);
op[u] = s[c1];
return u;
}
注意上述程式碼是如何尋找“最後一個運算子”的。程式碼裡用了一個變數p,只有當p=0時才考慮這個運算子。為什麼呢?因為括號裡的運算子一定不是最後計算的,應當忽略。例如(a+b)*c中雖然有一個加號,但卻是在括號裡的,實際上比它優先順序高的乘號才是最後計算的。由於加減和乘除號都是左結合的,最後一個運算子才是最後計算的,所以用兩個變數c1和c2分別記錄“最右”出現的加減號和乘除號。
再接下來的程式碼就不難理解了:如果括號外有加減號,它們肯定最後計算;但如果沒有加減號,就需要考慮乘除號( if(c1<0) c1 = c2 );如果全都沒有,說明整個表示式外面被一對括號括起來,把它去掉後遞迴呼叫。這樣,就找到了最後計算的運算子s[c1],它的左子樹是區間[x, c1],右子樹是區間[c1+1, y]。
提示:建立表示式樹的一種方法是每次找到最後的運算子,然後遞迴建樹。“最後計算”的運算子是在括號外的、優先順序最低的運算子。如果有多個,根據結合性來選擇:左結合的(如加減乘除)選最右邊;右結合的(如乘方)選最左邊。根據規定,優先順序相同的運算子的結合性總是相同。
字尾表示式計算程式碼實現
這個程式碼十分簡單,只要將演算法直譯過來即是程式碼,博主比較懶,就將這個工作交給讀者了,如果學校裡後面有這個作業,博主會貼上程式碼。。