資料庫之函式依賴
前言
今天又重新拾起了《資料庫系統原理》,因為之前對它學的不夠紮實,所以現在需要重新進行深入的學習,函式依賴這一部分雖然不是特別難,但是我就是有點“迷”,老是有點弄不清楚,所以今天抽出點時間“收拾”他一下,下面和大家分享一下“收拾過程”!!!
收拾過程
- 什麼是函式依賴?
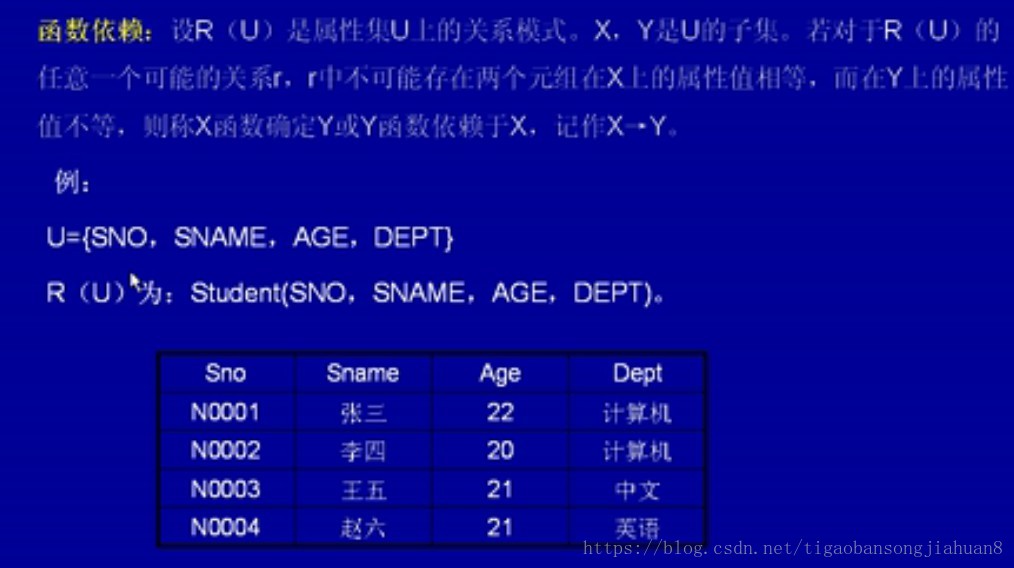
- 定義:設一個關係為R(U),X和Y為屬性集U上的子集,若對於X上的每個值都有Y上的一個唯一值與之對應,則稱X和Y具有函式依賴關係,並稱X 函式決定Y,或稱Y函式依賴於X,記作X→Y,稱X為決定因素。
- 簡單地說,函式依賴就是:知道A可以確切的找到B,這樣的函式叫做函式依賴。其實就是單值函式:例如:f(x)=2x(PS:後面會有詳細的示例說明)
- 示例:
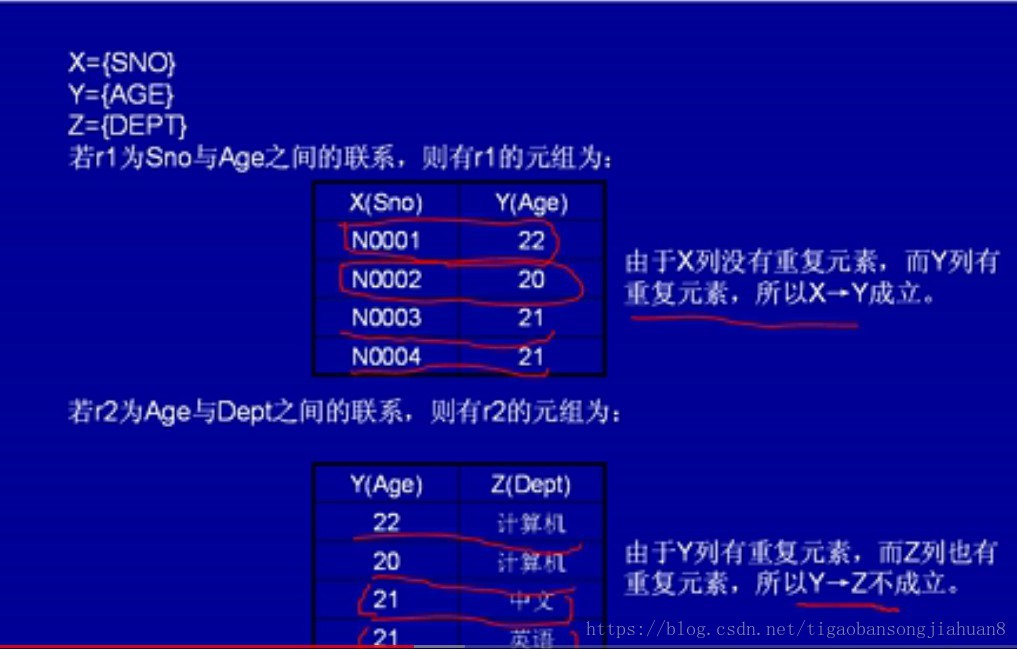
如通過學號和專業兩個屬性,1號可以確定是計算機(是函式依賴),但是通過年齡和專業這兩個屬性來判斷,21歲,有中文,有英文,不能確定下來(不是函式依賴) 什麼是完全函式依賴?
- 示例:
SC(S#,C#,GRADE) 說明:S#:學號,C#:課程號,GRADE:成績,S#→\C#,S#→\GRADE,單個屬性不能作為決定因素,但是組合起來可以,即(S#,C#)→GRADE,注:(S#,C#)相當於X,GRADE相當於Y。
- 示例:
什麼是部分函式依賴?
定義:設一個關係為R(U),X和Y為屬性集U上的子集,若存在X→Y,同時X的一個真子集X’也能夠函式決定Y,即存在X’→Y,則稱X→Y的函式依賴為部分函式依賴,或者說,X部分函式決定Y,Y部分函式依賴於X;否則若在X中不存在一個真子集X’,使得X’也能夠函式決定Y,則稱X完全函式決定Y,或Y完全函式依賴於X。X→Y的部分函式依賴也稱為區域性函式依賴。
示例:
| 職工號 | 姓名 | 性別 | 年齡 | 職務 |
|---|---|---|---|---|
| 1001 | 張三 | 男 | 36 | 正處 |
| 1002 | 李四 | 男 | 38 | 副處 |
| 1003 | 王五 | 男 | 50 | 正科 |
| 1004 | 趙六 | 女 | 38 | 副處 |
| 1005 | 孫七 | 女 | 49 | 科員 |
上述職工關係中,職工號和其他每個屬性之間的函式依賴都是完全函式依賴,以為職工號是一個單屬性決定因素,他不可能在包含其他任何屬性,那麼就不存在真子集函式決定其他每個屬性的情況存在,如(職工號,性別)的值雖然能夠決定相應職工的年齡,但其中的真子集“職工號”就能夠函式決定其年齡,所以(職工號,性別)到年齡之間的函式為部分函式依賴(因為只通過“職工號”就可以決定)。(簡單的說:真子集可以決定結果)
什麼是傳遞函式依賴?
定義:一個關係R(U),X,Y,Z為屬性集U上的子集,其中存在X→Y和Y→Z,但Y不決定X,同時Y不包含Z,則存在X→Z,即X傳遞函式決定Z,Z傳遞函式依賴於X。
注意:在這裡強調的是Y不反過來函式決定X,因為如果X→Y,同時Y→X,則X和Y為相互決定的函式依賴關係,記做“X←→Y”,這樣X和Y是等價的,在函式依賴中是可以相互轉化的,X→Z就是直接函式依賴,而不是傳遞函式依賴了。- 示例:
如:設一個學生關係為(學號,姓名,性別,系號,系名,系主任名),一般每個學生只屬於一個系,每個繫有許多學生,每個系都對應唯一的系名和系主任名。
傳遞函式依賴分析:在該關係中,學號能夠函式決定姓名、性別和系號,即存在“學號→姓名”、“學號→性別”、“學號→系號”,系號又能夠函式決定系名和系主任名,即存在“系號→系名”和“系號→系主任名”。由於學號決定系號,系號又決定系名和系主任名,所以給定一個學號之後也就能夠唯一對應一個系名或系主任名,也就是說,在學生關係中還存在“學號→系名”和“學號→系主任名”這兩個函式依賴是傳遞函式依賴。
- 示例:
什麼是最小函式依賴?
- 定義:設一個關係為R(U),X和Y為U的子集,若X→Y為完全函式依賴,同時Y為單屬性,則稱X→Y為R的最小函式依賴。由R中所有最小函式依賴構成R的最小函式依賴集,並且在最小函式依賴集中不應含有冗餘的傳遞函式依賴。
- 示例:
- 設一個關係為R(A,B,C,D),它的函式依賴集為FD={A→B,B→C,A→C,B→D},判斷它是否為R的最小函式依賴集。
- 分析:由FD中的A→B和B→C可得到A→C,也就是說A→B和B→C中已經蘊涵A→C,所以給出的A→C是冗餘的,應去掉。原FD不是R的一個最小依賴集,若修改為FD={A→B,B→C,B→D},就成為R的最小函式依賴集。
如何根據函式依賴求出關係中的侯選碼?
- 定義:設一個關係為R(U),X為U的一個子集,若X能夠函式決定U中的每個屬性,並且X的任何真子集都不能函式決定U中的每個屬性,則稱X為關係R的一個候選碼。
- 解析:
- 由於一個候選碼能夠函式決定關係中的每個屬性,根據函式依賴的合併規則,可知候選碼能夠函式決定整個元組,即所有屬性。也可以說:若關係中的一個屬性或屬性組能夠函式決定整個元組,並且它的任何子集都不能函式決定整個元組,則它被稱為該關係的一個候選碼。
- 示例一:
- 在上面介紹過的職工關係中,職工號屬效能夠函式決定職工號、姓名、性別、年齡、職務等所有屬性,並且職工號為單屬性,不可再分,肯定不會存在任何子集能夠函式決定整個元組,所以職工號為該關係的一個候選碼;若在該關係中還帶有身份證號屬性,則身份證號屬性的每一個值也能夠唯一標識一個元組,所以也能夠函式決定關係中的所有屬性,因此身份證號也是一個候選碼。
- 示例二:
- 設一個教學關係為(教師號,姓名,課程號,課程名,課程學分,專業號,專業名,教學等級分),假定每個教師有一個唯一的教師號,每門課程有一個唯一的課程號,每個專業有一個唯一的專業號,每個教師號對應一個姓名,每個課程號對應一個課程名和一個課程學分,每個專業號對應一個專業名,教學等級分是根據某個教師給某個專業上某門課程的教學評價效果而得到的分數,每個教師可以給不同的專業上不同的課程,請通過函式依賴分析,求出該關係的候選碼。
- 分析:
- FD={教師號→姓名,課程號→課程名,課程號→課程學分,專業號→專業名,(教師號,課程號,專業號)→教學等級分}。
由FD可以看出,只有(教師號,課程號,專業號)能夠函式決定每個屬性,並且它的任何真子集都不能函式決定每個屬性,所以(教師號,課程號,專業號)是該關係的唯一一個候選碼。
- FD={教師號→姓名,課程號→課程名,課程號→課程學分,專業號→專業名,(教師號,課程號,專業號)→教學等級分}。
什麼是平凡和非平凡函式依賴?
- 定義:設一個關係為R(U),X和Y為屬性集U上的子集,若X→Y且X不包含Y,則稱X→Y為非平凡函式依賴,否則若X Y則必有X→Y,稱此X→Y 為平凡函式依賴。
- 分析:在一個職工關係中,職工號總能函式決定它本身,記作“職工號→職工號”,對於任一個給定的職工號,都有它本身的職工號值唯一對應,此為平凡函式依賴。又如:職工號和性別構成的屬性子集總是能夠函式決定其中的職工號或性別屬性,可分別記作為“(職工號,性別)→職工號”和“(職工號,性別)→性別”,因為對於任何給定的一個元組中的職工號和性別的組合值,都唯一對應一個職工號值或性別值,不可能出現其他的職工號值或性別值,此種也為平凡函式依賴。
- 非平凡函式依賴,即X→Y且X Y。如在職工關係中,職工號函式決定其他每個屬性都是非平凡函式依賴,另外“(職工號,姓名)→性別”也是非平凡函式依賴,雖然在這裡由決定因素中所含的職工號單屬性就能夠函式決定性別,而帶有的姓名屬性有些多餘。
小結
這一部分總算是總結完了,可以告一小段落了,這回自己原來不明白的地方現在都清楚了,這些都是自己對這一部分的理解,可能會有些許出入,但是還是希望能幫助到一些需要幫助的人,同時也歡迎大家在下方評論區留言,互相交流一下!!!